Intuitioner om L1- och L2-regularisering
On september 20, 2021 by admin0) Vad är L1 och L2?
L1- och L2-regularisering har sitt namn efter L1- och L2-normen för en vektor w. Här finns en grundbok om normer:
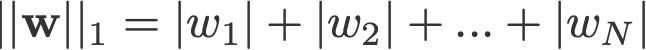


<förändra log: missade att ta absolutvärdena för 2-norm och p-norm>
En linjär regressionsmodell som tillämpar L1-norm för regularisering kallas lassoregression, och en modell som tillämpar (kvadrerad) L2-norm för regularisering kallas ridge-regression. För att implementera dessa två, observera att den linjära regressionsmodellen förblir densamma:
men det är beräkningen av förlustfunktionen som inkluderar dessa regulariseringstermer:

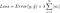


Anmärkning: Strängt taget är den sista ekvationen (ridge-regression) en förlustfunktion med kvadrerad L2-norm för vikterna (lägg märke till avsaknaden av kvadratroten). (Tack Max Pechyonkin för att du belyste detta!)
Regulariseringstermerna är ”begränsningar” som en optimeringsalgoritm måste ”följa” när den minimerar förlustfunktionen, bortsett från att den måste minimera felet mellan det sanna y och det förutspådda ŷ.
1) Modell
Låtsas vi definiera en modell för att se hur L1 och L2 fungerar. För enkelhetens skull definierar vi en enkel linjär regressionsmodell ŷ med en oberoende variabel.
Här har jag använt mig av deep learning-konventionerna w (”weight”) och b (”bias”).
I praktiken är enkla linjära regressionsmodeller inte benägna att överanpassas. Som nämndes i inledningen är djupinlärningsmodeller mer mottagliga för sådana problem på grund av deras modellkomplexitet.
Som sådan bör du notera att de uttryck som används i den här artikeln lätt kan utvidgas till mer komplexa modeller, som inte är begränsade till linjär regression.
2) Förlustfunktioner
För att demonstrera effekten av L1- och L2-regularisering, låt oss anpassa vår linjära regressionsmodell med hjälp av tre olika förlustfunktioner/mål:
- L
- L1
- L2
Vårt mål är att minimera dessa olika förluster.
2.1) Förlustfunktion utan regularisering
Vi definierar förlustfunktionen L som det kvadrerade felet, där felet är skillnaden mellan y (det sanna värdet) och ŷ (det förutspådda värdet).

Låtsas oss anta att vår modell kommer att bli överanpassad med denna förlustfunktion.
2.2) Förlustfunktion med L1-regularisering
Baserat på ovanstående förlustfunktion ser det ut så här om man lägger till en L1-regulariseringsterm till den:

där regulariseringsparametern λ > 0 är manuellt inställd. Vi kallar denna förlustfunktion för L1. Observera att |w| är differentierbar överallt utom när w=0, vilket visas nedan. Vi kommer att behöva detta senare.

2.3) Förlustfunktion med L2-regularisering
Samma sak om man lägger till en L2-regulariseringsterm till L ser ut så här:

där återigen λ > 0.
3) Gradient Descent
Nu ska vi lösa den linjära regressionsmodellen med hjälp av gradient descent-optimering baserad på de tre förlustfunktioner som definierats ovan. Minns att uppdatering av parametern w i gradient descent sker enligt följande:
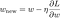
Låt oss ersätta den sista termen i ovanstående ekvation med gradienten för L, L1 och L2 w.r.t. w.
L:

L1:

L2:

4) Hur förhindras överanpassning?
Från och med nu utför vi följande substitutioner på ekvationerna ovan (för bättre läsbarhet):
- η = 1,
- H = 2x(wx+b-y)
vilket ger oss
L:

L1:
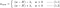
L2:
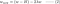
4.1) Med vs. utan regularisering
Observera skillnaderna mellan viktuppdateringarna med regulariseringsparametern λ och utan den. Här är några intuitioner.
Intuition A:
Säg att med ekvation 0 ger beräkning av w-H ett w-värde som leder till överanpassning. Då kommer ekvationerna {1.1, 1.2 och 2} intuitivt att minska risken för överanpassning eftersom införandet av λ gör att vi flyttar oss bort från just det w-värde som skulle ge oss problem med överanpassning i föregående mening.
Intuition B:
Låt oss säga att en överanpassad modell innebär att vi har ett w-värde som är perfekt för vår modell. ”Perfekt” betyder att om vi ersätter data (x) tillbaka i modellen kommer vår förutsägelse ŷ att ligga mycket, mycket nära det sanna y. Visst, det är bra, men vi vill inte ha perfekt. Varför? Därför att detta innebär att vår modell endast är avsedd för det dataset som vi tränade på. Detta innebär att vår modell kommer att ge förutsägelser som ligger långt ifrån det sanna värdet för andra dataset. Så vi nöjer oss med mindre än perfekt, med förhoppningen att vår modell också kan få nära förutsägelser med andra data. För att göra detta ”smutsar” vi ner detta perfekta w i ekvation 0 med en straffterm λ. Detta ger oss ekvationerna {1.1, 1.2 och 2}.
Intuition C:
Bemärk att H (enligt definitionen här) är beroende av modellen (w och b) och data (x och y). Uppdatering av vikterna baserat enbart på modellen och data i ekvation 0 kan leda till överanpassning, vilket leder till dålig generalisering. I ekvationerna {1.1, 1.2 och 2} å andra sidan påverkas slutvärdet av w inte bara av modellen och uppgifterna, utan också av en fördefinierad parameter λ som är oberoende av modellen och uppgifterna. Vi kan således förhindra överanpassning om vi fastställer ett lämpligt värde på λ, även om ett för stort värde kommer att leda till att modellen blir allvarligt underanpassad.
Intuition D:
Edden Gerber (tack!) har gett oss en intuition om i vilken riktning vår lösning håller på att förskjutas. Ta en titt i kommentarerna: https://medium.com/@edden.gerber/thanks-for-the-article-1003ad7478b2
4.2) L1 vs L2
Vi ska nu fokusera vår uppmärksamhet på L1 och L2 och skriva om ekvationerna {1.1, 1.2 och 2} genom att omordna deras λ- och H-termer på följande sätt:
L1:
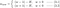
L2:
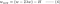
Genomför den andra termen i varje ekvation ovan. Förutom H beror förändringen av w på termen ±λ eller termen -2λw, vilket belyser inflytandet av följande:
- Signalen för aktuellt w (L1, L2)
- Magnituden för aktuellt w (L2)
- Dubbling av regulariseringsparametern (L2)
Om viktuppdateringar med hjälp av L1 påverkas av den första punkten påverkas viktuppdateringar från L2 av alla de tre punkterna. Även om jag har gjort denna jämförelse bara baserat på den iterativa ekvationsuppdateringen, observera att detta inte betyder att den ena är ”bättre” än den andra.
För tillfället ska vi nedan se hur en regulariseringseffekt från L1 kan uppnås bara genom tecknet på den aktuella w.
4.3) L1:s effekt på att trycka mot 0 (gleshet)
Ta en titt på L1 i ekvation 3.1. Om w är positiv kommer regulariseringsparametern λ>0 att driva w till att bli mindre positiv, genom att subtrahera λ från w. Omvänt i ekvation 3.2, om w är negativ, kommer λ att läggas till w, vilket driver den till att bli mindre negativ. Detta leder alltså till att w pressas mot 0.
Detta är naturligtvis meningslöst i en linjär regressionsmodell med en enda variabel, men kommer att visa sin förmåga att ”ta bort” onödiga variabler i multivariata regressionsmodeller. Du kan också se L1 som att minska antalet funktioner i modellen helt och hållet. Här är ett godtyckligt exempel på hur L1 försöker ”skjuta” några variabler i en multivariat linjär regressionsmodell:
Hur hjälper det till med att skjuta w mot 0 när det gäller överanpassning i L1-reglering? Som nämnts ovan minskar vi antalet funktioner när w går mot 0 genom att minska variabelns betydelse. I ekvationen ovan ser vi att x_2, x_4 och x_5 är nästan ”värdelösa” på grund av sina små koefficienter, och därför kan vi ta bort dem från ekvationen. Detta minskar i sin tur modellens komplexitet, vilket gör vår modell enklare. En enklare modell kan minska risken för överanpassning.
Anm.
Och även om L1 påverkar vikterna mot 0 och L2 inte gör det, innebär detta inte att vikterna inte kan nå nära 0 på grund av L2.
Lämna ett svar