Intuitions on L1 and L2 Regularisation

0) What’s L1 and L2?

L1 and L2 regularisation owes its name to L1 and L2 norm of a vector w respectively. Oto elementarz na temat norm:

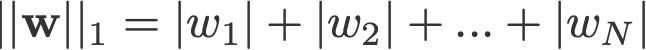
<change log: missed out taking the absolutes for 2-norm and p-norm>

Model regresji liniowej, który implementuje normę L1 do regularności, nazywa się regresją lasso, a taki, który implementuje (kwadratową) normę L2 do regularności, nazywa się regresją ridge. Aby zaimplementować te dwa, zauważ, że model regresji liniowej pozostaje taki sam:

, ale to obliczenie funkcji straty zawiera te warunki regularyzacji:

.

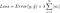
Uwaga: Ściśle mówiąc, ostatnie równanie (regresja grzbietowa) jest funkcją straty z kwadratową normą L2 wag (zauważ brak pierwiastka kwadratowego). (Dziękuję Maxowi Pechyonkinowi za zwrócenie na to uwagi!)

Wyrażenia regularyzacyjne są „ograniczeniami”, których algorytm optymalizacyjny musi „przestrzegać” podczas minimalizacji funkcji straty, poza koniecznością minimalizacji błędu między prawdziwym y a przewidywanym ŷ.

1) Model

Zdefiniujmy model, aby zobaczyć, jak działają L1 i L2. Dla uproszczenia definiujemy prosty model regresji liniowej ŷ z jedną zmienną niezależną.

W tym miejscu użyłem konwencji głębokiego uczenia w („weight”) i b („bias”).

W praktyce proste modele regresji liniowej nie są podatne na przepełnienie. Jak wspomniano we wstępie, modele głębokiego uczenia są bardziej podatne na takie problemy ze względu na złożoność modelu.

Jako takie, zwróć uwagę, że wyrażenia użyte w tym artykule są łatwo rozszerzalne na bardziej złożone modele, nie ograniczone do regresji liniowej.

2) Funkcje straty

Aby zademonstrować efekt regularyzacji L1 i L2, dopasujmy nasz model regresji liniowej przy użyciu 3 różnych funkcji straty/celów:

• L
• L1
• L2

Naszym celem jest minimalizacja tych różnych strat.

2.1) Funkcja straty bez regularności

Zdefiniujemy funkcję straty L jako błąd podniesiony do kwadratu, gdzie błąd jest różnicą między y (wartość prawdziwa) i ŷ (wartość przewidywana).

Załóżmy, że nasz model będzie przepełniony przy użyciu tej funkcji straty.

2.2) Funkcja straty z regularyzacją L1

Bazując na powyższej funkcji straty, dodanie do niej terminu regularyzacji L1 wygląda następująco:

gdzie parametr regularyzacji λ > 0 jest ręcznie dostrajany. Nazwijmy tę funkcję straty L1. Zauważmy, że |w| jest różniczkowalna wszędzie z wyjątkiem sytuacji, gdy w=0, jak pokazano poniżej. Będzie nam to potrzebne później.

2.3) Funkcja straty z regularyzacją L2

Podobnie, dodanie do L członu regularyzującego L2 wygląda tak:

gdzie znów λ > 0.

3) Zejście gradientowe

Teraz rozwiążmy model regresji liniowej za pomocą optymalizacji zejścia gradientowego w oparciu o 3 funkcje straty zdefiniowane powyżej. Przypomnijmy, że aktualizacja parametru w w procesie zstępowania gradientowego przebiega następująco:

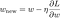
Zastąpmy ostatni człon powyższego równania gradientem L, L1 i L2 w.r.t. w.

L:

L1:

L2:

4) Jak zapobiega się overfittingowi?

Od tego miejsca wykonajmy następujące podstawienia na powyższych równaniach (dla lepszej czytelności):

• η = 1,
• H = 2x(wx+b-y)

co daje nam

L:

L1:

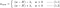
L2:

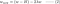
4.1) Z regularyzacją vs. bez regularyzacji

Zauważ różnice pomiędzy aktualizacjami wag z parametrem regularyzacji λ i bez niego. Oto kilka intuicji.

Intuicja A:

Powiedzmy, że przy równaniu 0, obliczanie w-H daje nam wartość w, która prowadzi do przepasowania. Wtedy, intuicyjnie, równania {1.1, 1.2 i 2} zmniejszą szanse na przepasowanie, ponieważ wprowadzenie λ sprawia, że odchodzimy od tego właśnie w, które w poprzednim zdaniu miało spowodować problemy z przepasowaniem.

Intuicja B:

Powiedzmy, że przepasowany model oznacza, że mamy wartość w, która jest idealna dla naszego modelu. 'Doskonała’ oznacza, że jeśli zastąpimy dane (x) z powrotem w modelu, nasza prognoza ŷ będzie bardzo, bardzo blisko prawdziwego y. Jasne, to dobrze, ale nie chcemy doskonałości. Dlaczego? Ponieważ oznacza to, że nasz model jest przeznaczony tylko dla zbioru danych, na którym trenowaliśmy. Oznacza to, że nasz model będzie produkował przewidywania, które są dalekie od prawdziwej wartości dla innych zbiorów danych. Więc zadowalamy się mniej niż doskonałym, z nadzieją, że nasz model może również uzyskać bliskie przewidywania z innymi danymi. Aby to zrobić, „zanieczyszczamy” to doskonałe w w równaniu 0 za pomocą terminu karnego λ. Daje nam to równania {1.1, 1.2 i 2}.

Intuicja C:

Zauważ, że H (jak zdefiniowano tutaj) zależy od modelu (w i b) i danych (x i y). Aktualizacja wag na podstawie tylko modelu i danych w Równaniu 0 może prowadzić do przepasowania, co prowadzi do słabego uogólnienia. Z drugiej strony, w równaniach {1.1, 1.2 i 2} na ostateczną wartość w wpływa nie tylko model i dane, ale także predefiniowany parametr λ, który jest niezależny od modelu i danych. Dzięki temu możemy uniknąć przepasowania, jeśli ustawimy odpowiednią wartość λ, choć zbyt duża wartość spowoduje poważne niedopasowanie modelu.

Intuicja D:

Edden Gerber (dzięki!) podał intuicję dotyczącą kierunku, w którym przesuwa się nasze rozwiązanie. Zajrzyjcie do komentarzy: https://medium.com/@edden.gerber/thanks-for-the-article-1003ad7478b2

4.2) L1 vs. L2

Skupimy teraz naszą uwagę na L1 i L2, i przepiszemy równania {1.1, 1.2 i 2} poprzez uporządkowanie ich członów λ i H w następujący sposób:

L1:

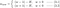
L2:

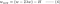
Porównaj drugi człon każdego z powyższych równań. Oprócz H, zmiana w zależy od terminu ±λ lub terminu -2λw, które podkreślają wpływ następujących czynników:

1. znaku aktualnego w (L1, L2)
2. wielkości aktualnego w (L2)
3. podwojenia parametru regularności (L2)

O ile na aktualizacje wag przy użyciu L1 wpływa pierwszy punkt, o tyle na aktualizacje wag z L2 wpływają wszystkie trzy punkty. Chociaż dokonałem tego porównania tylko w oparciu o iteracyjną aktualizację równań, proszę zauważyć, że nie oznacza to, że jedno jest „lepsze” od drugiego.

Na razie zobaczmy poniżej, jak efekt regularyzacji z L1 może być osiągnięty tylko przez znak bieżącego w.

4.3) Efekt L1 na spychanie w kierunku 0 (sparsity)

Spójrzmy na L1 w równaniu 3.1. Jeśli w jest dodatnie, parametr regularyzacji λ>0 spowoduje, że w będzie mniej dodatnie, poprzez odjęcie λ od w. I odwrotnie, w równaniu 3.2, jeśli w jest ujemne, λ zostanie dodane do w, powodując, że będzie mniej ujemne. W związku z tym ma to wpływ na popychanie w w kierunku 0.

Jest to oczywiście bezcelowe w 1-zmiennym modelu regresji liniowej, ale udowodni swoją sprawność w „usuwaniu” bezużytecznych zmiennych w modelach regresji wielorakiej. Możesz również myśleć o L1 jako o redukcji liczby cech w modelu. Oto arbitralny przykład L1 próbującej 'wypchnąć’ niektóre zmienne w modelu regresji liniowej:

W jaki więc sposób wypychanie w w kierunku 0 pomaga w przepasowaniu w regularyzacji L1? Jak wspomniano powyżej, gdy w zmierza do 0, zmniejszamy liczbę cech poprzez zmniejszenie ważności zmiennej. W powyższym równaniu widzimy, że x_2, x_4 i x_5 są prawie „bezużyteczne” ze względu na ich małe współczynniki, stąd możemy je usunąć z równania. To z kolei zmniejsza złożoność modelu, czyniąc nasz model prostszym. Prostszy model może zmniejszyć szanse na przepasowanie.

Uwaga

Choć L1 ma wpływ na spychanie wag w kierunku 0, a L2 nie, nie oznacza to, że wagi nie są w stanie zbliżyć się do 0 z powodu L2.

.