Intuïties over L1 en L2 regularisatie
On september 20, 2021 by admin0) Wat is L1 en L2?
L1 en L2 regularisatie dankt zijn naam aan respectievelijk de L1 en L2 norm van een vector w. Hier is een inleiding over normen:
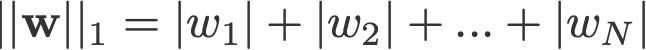


<wijzig log: gemist bij het nemen van de absoluten voor 2-norm en p-norm>
Een lineair regressiemodel dat de L1-norm voor regularisatie implementeert, wordt lasso-regressie genoemd, en een model dat de (gekwadrateerde) L2-norm voor regularisatie implementeert, wordt ridge-regressie genoemd. Om deze twee te implementeren, moet worden opgemerkt dat het lineaire regressiemodel hetzelfde blijft:
maar het is de berekening van de verliesfunctie die deze regularisatietermen omvat:

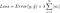

Noot: Strikt genomen is de laatste vergelijking (ridge regression) een verliesfunctie met gekwadrateerde L2-norm van de gewichten (let op de afwezigheid van de vierkantswortel). (Met dank aan Max Pechyonkin die hierop heeft gewezen!)
De regularisatietermen zijn “beperkingen” waaraan een optimalisatiealgoritme zich moet “houden” bij het minimaliseren van de verliesfunctie, afgezien van het feit dat de fout tussen de ware y en de voorspelde ŷ moet worden geminimaliseerd.
1) Model
Laten we een model definiëren om te zien hoe L1 en L2 werken. Voor de eenvoud definiëren we een eenvoudig lineair regressiemodel ŷ met één onafhankelijke variabele.

Hierbij heb ik de deep learning conventies w (‘gewicht’) en b (‘bias’) gebruikt.
In de praktijk zijn eenvoudige lineaire regressiemodellen niet vatbaar voor overfitting. Zoals in de inleiding is vermeld, zijn deep learning-modellen vatbaarder voor dergelijke problemen vanwege hun modelcomplexiteit.
Merk daarom op dat de uitdrukkingen die in dit artikel worden gebruikt, gemakkelijk kunnen worden uitgebreid tot complexere modellen, die niet beperkt zijn tot lineaire regressie.
2) Verliesfuncties
Om het effect van L1- en L2-regularisatie aan te tonen, laten we ons lineaire regressiemodel passen met 3 verschillende verliesfuncties/doelstellingen:
- L
- L1
- L2
Onze doelstelling is om deze verschillende verliezen te minimaliseren.
2.1) Verliesfunctie zonder regularisatie
We definiëren de verliesfunctie L als de gekwadrateerde fout, waarbij de fout het verschil is tussen y (de werkelijke waarde) en ŷ (de voorspelde waarde).

Laten we aannemen dat ons model met behulp van deze verliesfunctie overgefitted zal worden.
2.2) Verliesfunctie met L1-regularisatie
Op basis van bovenstaande verliesfunctie ziet het er als volgt uit als we er een L1-regularisatieterm aan toevoegen:

waarbij de regularisatieparameter λ > 0 handmatig wordt afgesteld. Laten we deze verliesfunctie L1 noemen. Merk op dat |w| overal differentieerbaar is, behalve wanneer w=0, zoals hieronder is aangegeven. We zullen dit later nodig hebben.

2.3) Verliesfunctie met L2-regularisatie
Ook het toevoegen van een L2-regulariseringsterm aan L ziet er als volgt uit:

waar ook hier geldt dat λ > 0.
3) Gradient Descent
Nu gaan we het lineaire regressiemodel oplossen met behulp van gradient descent-optimalisatie op basis van de 3 hierboven gedefinieerde verliesfuncties. Bedenk dat het bijwerken van de parameter w bij gradiëntafdaling als volgt verloopt:
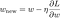
Laten we de laatste term in de bovenstaande vergelijking vervangen door de gradiënt van L, L1 en L2 w.r.t. w.
L:

L1:

L2:

4) Hoe wordt overfitting voorkomen?
Vanaf hier voeren we de volgende substituties uit op de bovenstaande vergelijkingen (voor een betere leesbaarheid):
- η = 1,
- H = 2x(wx+b-y)
wat ons
L oplevert:

L1:
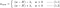
L2:
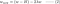
4.1) Met vs. Zonder regularisatie
Bekijk de verschillen tussen de gewichtsupdates met de regularisatieparameter λ en zonder. Hier volgen enkele intuïties.
Intuïtie A:
Laten we zeggen dat met Vergelijking 0, het berekenen van w-H ons een w-waarde oplevert die tot overfitting leidt. Dan zullen, intuïtief, vergelijkingen {1.1, 1.2 en 2} de kans op overfitting verkleinen, omdat het introduceren van λ ons wegleidt van precies die w die ons in de vorige zin tot overfittingproblemen ging leiden.
Intuïtie B:
Laten we zeggen dat een overgefitted model betekent dat we een w-waarde hebben die perfect is voor ons model. Perfect’ betekent dat als we de gegevens (x) terug in het model zouden plaatsen, onze voorspelling ŷ heel, heel dicht bij de ware y zal liggen. Waarom niet? Omdat dit betekent dat ons model alleen bedoeld is voor de dataset waarop we getraind hebben. Dit betekent dat ons model voorspellingen zal doen die ver van de ware waarde liggen voor andere datasets. Dus nemen we genoegen met minder dan perfect, in de hoop dat ons model ook met andere gegevens tot goede voorspellingen kan komen. Daartoe ‘besmetten’ we dit perfecte w in vergelijking 0 met een strafterm λ. Dit levert vergelijkingen {1.1, 1.2 en 2} op.
Intuïtie C:
Merk op dat H (zoals hier gedefinieerd) afhankelijk is van het model (w en b) en de gegevens (x en y). Het bijwerken van de gewichten alleen op basis van het model en de gegevens in vergelijking 0 kan leiden tot overfitting, wat een slechte generalisatie tot gevolg heeft. Anderzijds wordt in vergelijkingen {1.1, 1.2 en 2} de uiteindelijke waarde van w niet alleen beïnvloed door het model en de gegevens, maar ook door een vooraf bepaalde parameter λ die onafhankelijk is van het model en de gegevens. We kunnen dus overfitting voorkomen als we een geschikte waarde van λ instellen, hoewel een te grote waarde ertoe zal leiden dat het model ernstig wordt ondergefitted.
Intuïtie D:
Edden Gerber (bedankt!) heeft een intuïtie gegeven over de richting waarheen onze oplossing wordt verschoven. Kijk maar eens in de commentaren: https://medium.com/@edden.gerber/thanks-for-the-article-1003ad7478b2
4.2) L1 vs. L2
We zullen onze aandacht nu richten op L1 en L2, en vergelijkingen herschrijven {1.1, 1.2 en 2} door hun λ- en H-termen als volgt te herschikken:
L1:
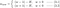
>
L2:
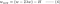
Vergelijk de tweede term van elk van de bovenstaande vergelijkingen. Afgezien van H hangt de verandering in w af van de term ±λ of de term -2λw, die de invloed van de volgende punten benadrukt:
- teken van de huidige w (L1, L2)
- magnitude van de huidige w (L2)
- verdubbeling van de regularisatieparameter (L2)
Wanneer de gewichtsupdates met behulp van L1 worden beïnvloed door het eerste punt, worden de gewichtsupdates met behulp van L2 beïnvloed door alle drie de punten. Hoewel ik deze vergelijking alleen op basis van de iteratieve vergelijking heb gemaakt, betekent dit niet dat de ene ‘beter’ is dan de andere.
Laten we nu eens zien hoe een regularisatie-effect van L1 kan worden bereikt door alleen het teken van de huidige w.
4.3) Het effect van L1 op het naar 0 duwen (sparsity)
Kijk eens naar L1 in vergelijking 3.1. Als w positief is, duwt de regularisatieparameter λ>0 w naar minder positief, door λ af te trekken van w. Omgekeerd, in vergelijking 3.2, als w negatief is, wordt λ toegevoegd aan w, waardoor het minder negatief wordt. Dit heeft dus tot gevolg dat w in de richting van 0 wordt geduwd.
Dit is natuurlijk zinloos in een lineair regressiemodel met 1 variabele, maar het zal zijn nut bewijzen om nutteloze variabelen te “verwijderen” in multivariate regressiemodellen. Je kan L1 ook zien als het verminderen van het aantal kenmerken in het model. Hier is een willekeurig voorbeeld van L1 dat probeert enkele variabelen in een multivariaat lineair regressiemodel te ‘duwen’:
Dus hoe helpt het duwen van w naar 0 bij overfitting in L1-regularisatie? Zoals hierboven vermeld, verminderen we het aantal kenmerken door het belang van de variabele te verminderen als w naar 0 gaat. In de bovenstaande vergelijking zien we dat x_2, x_4 en x_5 bijna “nutteloos” zijn vanwege hun kleine coëfficiënten, zodat we ze uit de vergelijking kunnen verwijderen. Dit vermindert op zijn beurt de complexiteit van het model, waardoor ons model eenvoudiger wordt. Een eenvoudiger model kan de kans op overfitting verkleinen.
Note
Wanneer L1 de invloed heeft om gewichten in de richting van 0 te duwen en L2 niet, betekent dit niet dat gewichten niet in de buurt van 0 kunnen komen als gevolg van L2.
Geef een antwoord