L1正則化とL2正則化の直観
On 9月 20, 2021 by admin0)L1、L2って何?
L1、L2正則化の名前は、それぞれベクトルwのL1、L2ノルムに起因しています。 ノルムについての入門書です。
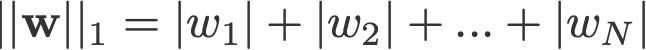

1-norm (L2>ノルム)。ノルム(L2ノルム、ユークリッドノルムとも)

<change log: 2-normとp-normの絶対値を取り損なった>
正則化にL1ノルムを実装した線形回帰モデルをlasso regression、正則化に(2乗)L2ノルムを実装したものをridge regressionと呼びます。 この2つを実装するために、線形回帰モデルはそのままで、
ただし、損失関数を計算するときに、この正規化の項も含まれることに注意してください。

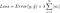

L2正則化による損失関数
注: 厳密には、最後の式(リッジ回帰)は重みのL2ノルムを2乗した損失関数である(平方根がないことに注意)。 (これを強調してくれた Max Pechyonkin に感謝!)
正則化項は、損失関数を最小化するときに最適化アルゴリズムが「遵守」しなければならない「制約」で、真の y と予測値 ŷ 間の誤差を最小化しなければならないこととは別に、
1) モデル
L1 と L2 がどう機能するかを見るためにモデルを定義することにする。 簡単のために、独立変数が1つの単純な線形回帰モデルŷを定義します。

ここでは深層学習の慣例のw(「重み」)とb(「偏り」)を使っています。
実際には、単純な線形回帰モデルはオーバーフィッティングになりにくいです。 冒頭で述べたように、深層学習モデルはモデルが複雑なため、そのような問題の影響を受けやすい。
そのため、この記事で使用した表現は、線形回帰に限らず、より複雑なモデルに容易に拡張できることに注意すること。
2) 損失関数
L1およびL2正則化の効果を示すために、3種類の損失関数/目的を使って線形回帰モデルをフィットさせてみましょう:
- L
- L1
- L2
我々の目的は、これらの損失を最小化することにあるのです。1)正則化なしの損失関数
損失関数Lを二乗誤差と定義し、誤差はy(真値)とŷ(予測値)の差とする。

この損失関数でモデルが過剰適合すると仮定しよう。
2.2) L1正則化のある損失関数
上記の損失関数にL1正則化の項を加えると次のようになる。

ここで正則化パラメータ λ > 0 は手動で調整される。 この損失関数をL1と呼ぶことにする。 なお、|w|は以下に示すように、w=0のときを除いてどこでも微分可能である。 これは後で必要になる。

2.3) L2正則化した損失関数
同様にLにL2正則化項を加えると次のようになる。

ここで再びλ > 0とする。
3) 勾配降下法
さて、上で定義した3つの損失関数に基づいて、勾配降下法による最適化で線形回帰モデルを解いてみよう。 勾配降下法でのパラメータwの更新は次のようになることを思い出してください:
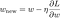
上式の最後の項にL、L1、L2のwの勾配を代入してみましょう。
L:

L1:

L2:

4) オーバーフィッティングはどのようにして防止するのでしょう?
ここからは、上の式に以下の代入をしてみましょう(読みやすくするため):
- η = 1,
- H = 2x(wx+b-y)
これにより
Lとなります。

L1:
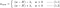
L2 が得られます。
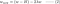
4.1) 正則化ありとなし
正則化パラメータλを用いた場合と用いない場合の重み更新の違いを観察してください。 以下は直感です。
直感A:
式0で、w-Hを計算すると、オーバーフィッティングにつながるw値が得られるとします。 すると、直感的に式{1.1,1.2,2}はオーバーフィットの可能性が低くなります。λを導入すると、前文でオーバーフィットの原因となったwから離れるからです。
Intuition B:
オーバーフィットモデルとは、モデルにとって最適のw値があることだとしましょう。 完璧」とは、データ (x) をモデルに代入すると、予測値 ŷ が真の y に非常に近くなることを意味します。 なぜか? なぜなら、これは我々のモデルが学習したデータセットにしか使えないことを意味するからです。 つまり、このモデルは他のデータセットでは真の値からかけ離れた予測をすることになる。 そこで、私たちは、モデルが他のデータでも近い予測ができることを期待して、完璧でないほうに落ち着きます。 これを行うには、式0におけるこの完璧なwをペナルティ項λで「汚す」。 これにより、式{1.1, 1.2 and 2}が得られる。
直観C:
H(ここで定義)はモデル(wとb)およびデータ(xとy)に依存していることに注意する。 式0においてモデルとデータのみに基づいて重みを更新すると、オーバーフィッティングになり、汎化がうまくいかなくなる可能性がある。 一方、式{1.1, 1.2, 2}では、wの最終値はモデルやデータだけでなく、モデルやデータから独立した定義済みのパラメータλにも影響される。 したがって、λの値を適切に設定すればオーバーフィットを防ぐことができますが、大きすぎるとモデルが著しくアンダーフィットしてしまいます。
直観D:
Edden Gerber (thanks!) は、我々の解がシフトしている方向について直観を提供してくれています。 コメントでご覧ください。 https://medium.com/@edden.gerber/thanks-for-the-article-1003ad7478b2
4.2) L1 vs. L2
ここで、L1 と L2 に注目し、式 {1.1, 1.2} を書き換えてみましょう。2と2}を、それらのλ項とH項を次のように並べ替えて書き直す:
L1:
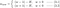
L2:
L2:
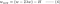
上の各式の第2項を比べてみてください。 H以外に、wの変化は±λの項または-2λwの項に依存し、以下の影響を強調する:
- 現在のwの符号 (L1, L2)
- 現在のwの大きさ (L2)
- 正規化パラメータの2倍 (L2)
L1による重み更新が1点目に影響を受けるのに対し、L2から重み更新は3点全てによって影響を受けていることがわかる。
とりあえず、現在のwの符号だけでL1による正則化の効果が得られることを以下に見てみましょう。
4.3) L1による0への押し出し効果(スパース性)
式3.1のL1を見てください。 wが正の場合、正則化パラメータλ>0はwからλを引いて、wをより正しくない方に押しやります。逆に式3.2では、wが負の場合、λをwに加えて、より負の方を押しやります。
これはもちろん1変数の線形回帰モデルでは無意味ですが、多変量回帰モデルでは無駄な変数を「除去」することに威力を発揮します。 また、L1 は、モデル内の特徴の数を完全に減らすと考えることもできます。 以下は、L1 が多変量線形回帰モデルでいくつかの変数を「押し出す」ことを試みる任意の例です:

では L1 正規化で w を 0 に向かって押せばオーバーフィットにどう貢献するのでしょうか。 上述したように、wが0になると、変数の重要度を下げることで特徴量を減らしているのです。 上の式では、x_2、x_4、x_5は係数が小さいため、ほとんど「役に立たない」ことがわかりますので、式から取り除くことができます。 これにより、モデルの複雑さが軽減され、モデルがより単純になります。
Note
L1は重みを0に近づける効果があり、L2はそうではないが、L2により重みが0に近づかないことを意味するわけではない。
コメントを残す