Istruzioni sulla regolarizzazione L1 e L2
Il Settembre 20, 2021 da admin0) Cos’è L1 e L2?
La regolarizzazione L1 e L2 deve il suo nome rispettivamente alla norma L1 e L2 di un vettore w. Ecco un primer sulle norme:
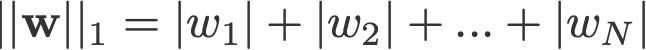


<cambia log: non ha preso gli assoluti per 2-norm e p-norm>
Un modello di regressione lineare che implementa la norma L1 per la regolarizzazione è chiamato regressione lasso, e uno che implementa la norma L2 (al quadrato) per la regolarizzazione è chiamato regressione ridge. Per implementare questi due, si noti che il modello di regressione lineare rimane lo stesso:
ma è il calcolo della funzione di perdita che include questi termini di regolarizzazione:

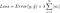

Nota: In senso stretto, l’ultima equazione (regressione di cresta) è una funzione di perdita con norma L2 quadrata dei pesi (notare l’assenza della radice quadrata). (Grazie Max Pechyonkin per averlo evidenziato!)
I termini di regolarizzazione sono ‘vincoli’ a cui un algoritmo di ottimizzazione deve ‘aderire’ quando minimizza la funzione di perdita, oltre a dover minimizzare l’errore tra il vero y e il predetto ŷ.
1) Modello
Definiamo un modello per vedere come L1 e L2 lavorano. Per semplicità, definiamo un semplice modello di regressione lineare ŷ con una variabile indipendente.

Qui ho usato le convenzioni di deep learning w (‘weight’) e b (‘bias’).
In pratica, i semplici modelli di regressione lineare non sono inclini all’overfitting. Come menzionato nell’introduzione, i modelli di deep learning sono più suscettibili a tali problemi a causa della loro complessità del modello.
Come tale, si noti che le espressioni utilizzate in questo articolo sono facilmente estendibili a modelli più complessi, non limitati alla regressione lineare.
2) Funzioni di perdita
Per dimostrare l’effetto della regolarizzazione L1 e L2, adattiamo il nostro modello di regressione lineare usando 3 diverse funzioni/obiettivi di perdita:
- L
- L1
- L2
Il nostro obiettivo è minimizzare queste diverse perdite.
2.1) Funzione di perdita senza regolarizzazione
Definiremo la funzione di perdita L come l’errore quadratico, dove l’errore è la differenza tra y (il valore vero) e ŷ (il valore predetto).

Prevediamo che il nostro modello sarà overfitted usando questa funzione di perdita.
2.2) Funzione di perdita con regolarizzazione L1
Sulla base della funzione di perdita di cui sopra, l’aggiunta di un termine di regolarizzazione L1 si presenta così:

dove il parametro di regolarizzazione λ > 0 viene regolato manualmente. Chiamiamo questa funzione di perdita L1. Si noti che |w| è differenziabile ovunque tranne quando w=0, come mostrato di seguito. Ne avremo bisogno in seguito.

2.3) Funzione di perdita con regolarizzazione L2
Similmente, aggiungendo un termine di regolarizzazione L2 a L appare così:

dove di nuovo, λ > 0.
3) Gradient Descent
Ora, risolviamo il modello di regressione lineare usando l’ottimizzazione gradient descent basata sulle 3 funzioni di perdita definite sopra. Ricordiamo che l’aggiornamento del parametro w nella discesa a gradiente è il seguente:
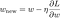
Sostituiamo l’ultimo termine dell’equazione precedente con il gradiente di L, L1 e L2 rispetto a w.
L:

L1:

L2:

4) Come si previene l’overfitting?
Da qui in poi, eseguiamo le seguenti sostituzioni sulle equazioni sopra (per una migliore leggibilità):
- η = 1,
- H = 2x(wx+b-y)
che ci danno
L:

L1:
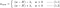
L2:
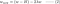
4.1) Con vs. Senza Regolarizzazione
Osserva le differenze tra gli aggiornamenti dei pesi con il parametro di regolarizzazione λ e senza. Ecco alcune intuizioni.
Intuizione A:
Diciamo che con l’equazione 0, il calcolo di w-H ci dà un valore di w che porta all’overfitting. Allora, intuitivamente, le equazioni {1.1, 1.2 e 2} ridurranno le possibilità di overfitting perché l’introduzione di λ ci fa allontanare proprio da quel w che ci avrebbe causato problemi di overfitting nella frase precedente.
Intuizione B:
Diciamo che un modello overfitted significa che abbiamo un valore w che è perfetto per il nostro modello. ‘Perfetto’ significa che se sostituiamo i dati (x) nel modello, la nostra previsione ŷ sarà molto, molto vicina al vero y. Certo, è buono, ma non vogliamo che sia perfetto. Perché? Perché questo significa che il nostro modello è destinato solo al set di dati su cui ci siamo addestrati. Questo significa che il nostro modello produrrà previsioni che sono molto lontane dal vero valore per altri set di dati. Quindi ci accontentiamo di meno della perfezione, con la speranza che il nostro modello possa ottenere previsioni vicine anche con altri dati. Per fare questo, “contaminiamo” questo w perfetto nell’equazione 0 con un termine di penalità λ. Questo ci dà le equazioni {1.1, 1.2 e 2}.
Intuizione C:
Nota che H (come definito qui) dipende dal modello (w e b) e dai dati (x e y). Aggiornare i pesi basati solo sul modello e sui dati nell’equazione 0 può portare a un overfitting, che porta a una scarsa generalizzazione. D’altra parte, nelle equazioni {1.1, 1.2 e 2}, il valore finale di w non è solo influenzato dal modello e dai dati, ma anche da un parametro predefinito λ che è indipendente dal modello e dai dati. Così, possiamo prevenire l’overfitting se impostiamo un valore appropriato di λ, anche se un valore troppo grande causerà un grave underfitting del modello.
Intuizione D:
Edden Gerber (grazie!) ha fornito un’intuizione sulla direzione verso cui la nostra soluzione viene spostata. Date un’occhiata nei commenti: https://medium.com/@edden.gerber/thanks-for-the-article-1003ad7478b2
4.2) L1 vs. L2
Ora concentriamo la nostra attenzione su L1 e L2, e riscriviamo le equazioni {1.1, 1.2 e 2} riorganizzando i loro termini λ e H come segue:
L1:
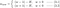
L2:
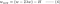
Confrontare il secondo termine di ciascuna delle equazioni precedenti. A parte H, il cambiamento di w dipende dal termine ±λ o dal termine -2λw, che evidenziano l’influenza di quanto segue:
- segno della corrente w (L1, L2)
- magnitudine della corrente w (L2)
- doppio del parametro di regolarizzazione (L2)
Mentre gli aggiornamenti dei pesi con L1 sono influenzati dal primo punto, quelli con L2 sono influenzati da tutti e tre i punti. Mentre ho fatto questo confronto solo sulla base dell’aggiornamento dell’equazione iterativa, si prega di notare che questo non significa che uno sia ‘migliore’ dell’altro.
Per ora, vediamo di seguito come un effetto di regolarizzazione da L1 può essere ottenuto solo dal segno dell’attuale w.
4.3) L’effetto di L1 sullo spingere verso 0 (sparsità)
Diamo un’occhiata a L1 nell’equazione 3.1. Se w è positivo, il parametro di regolarizzazione λ>0 spingerà w ad essere meno positivo, sottraendo λ da w. Viceversa nell’equazione 3.2, se w è negativo, λ sarà aggiunto a w, spingendolo ad essere meno negativo. Quindi, questo ha l’effetto di spingere w verso 0.
Questo è ovviamente inutile in un modello di regressione lineare a 1 variabile, ma dimostrerà la sua abilità nel ‘rimuovere’ variabili inutili nei modelli di regressione multivariata. Si può anche pensare a L1 come alla riduzione del numero di caratteristiche nel modello. Ecco un esempio arbitrario di L1 che cerca di ‘spingere’ alcune variabili in un modello di regressione lineare multivariata:
Perciò come spingere w verso 0 aiuta l’overfitting nella regolarizzazione L1? Come menzionato sopra, quando w va a 0, stiamo riducendo il numero di caratteristiche riducendo l’importanza della variabile. Nell’equazione sopra, vediamo che x_2, x_4 e x_5 sono quasi ‘inutili’ a causa dei loro piccoli coefficienti, quindi possiamo rimuoverli dall’equazione. Questo a sua volta riduce la complessità del modello, rendendo il nostro modello più semplice. Un modello più semplice può ridurre le possibilità di overfitting.
Note
Mentre L1 ha l’influenza di spingere i pesi verso lo 0 e L2 no, questo non implica che i pesi non siano in grado di arrivare vicino allo 0 a causa di L2.
Lascia un commento