Intuições sobre L1 e L2 Regularização
On Setembro 20, 2021 by admin0) O que é L1 e L2?
L1 e L2 regularização deve o seu nome à norma L1 e L2 de um vector w respectivamente. Aqui está uma cartilha sobre normas:
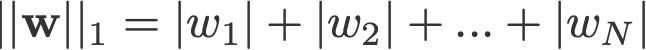


<log de mudança: falhou a tomada dos absolutos para 2-norm e p-norm>
Um modelo de regressão linear que implementa a norma L1 para regularização é chamado de regressão do laço, e um que implementa (ao quadrado) a norma L2 para regularização é chamado de regressão da crista. Para implementar estes dois, note que o modelo de regressão linear permanece o mesmo:
mas é o cálculo da função de perda que inclui estes termos de regularização:


Nota: Estritamente falando, a última equação (regressão da crista) é uma função de perda com a norma L2 quadrada dos pesos (note a ausência da raiz quadrada). (Obrigado Max Pechyonkin por realçar isto!)
Os termos de regularização são ‘restrições’ pelas quais um algoritmo de optimização deve ‘aderir’ ao minimizar a função de perda, além de ter que minimizar o erro entre o verdadeiro y e o previsto ŷ.
1) Modelo
Vamos definir um modelo para ver como L1 e L2 funcionam. Para simplificar, definimos um modelo simples de regressão linear ŷ com uma variável independente.

Aqui utilizei as convenções de aprendizagem profunda w (“peso”) e b (“viés”).
Na prática, os modelos simples de regressão linear não são propensos a sobreajustar. Como mencionado na introdução, os modelos de aprendizagem profunda são mais susceptíveis a tais problemas devido à sua complexidade.
Como tal, note que as expressões utilizadas neste artigo são facilmente estendidas a modelos mais complexos, não se limitando à regressão linear.
2) Funções de Perda
Para demonstrar o efeito da regularização L1 e L2, vamos ajustar o nosso modelo de regressão linear usando 3 diferentes funções/objectivos de perda:
- L
- L1
- L2
O nosso objectivo é minimizar estas diferentes perdas.
2.1) Função perda sem regularização
Definimos a função perda L como o erro quadrático, onde o erro é a diferença entre y (o valor verdadeiro) e ŷ (o valor previsto).

Vamos supor que o nosso modelo será sobreajustado usando esta função perda.
2.2) Função de perda com regularização L1
Baseada na função de perda acima, adicionando-lhe um termo de regularização L1 assim:

Onde o parâmetro de regularização λ > 0 é sintonizado manualmente. Vamos chamar a esta função de perda L1. Note que |w| é diferenciável em qualquer lugar, exceto quando w=0, como mostrado abaixo. Vamos precisar disto mais tarde.

2.3) Função perda com regularização L2
Simplesmente, adicionando um termo de regularização L2 a L parece assim:

Onde novamente, λ > 0.
3) Descida de gradiente
Agora, vamos resolver o modelo de regressão linear utilizando a optimização da descida de gradiente com base nas 3 funções de perda definidas acima. Lembre-se que a atualização do parâmetro w em descida de gradiente é a seguinte:
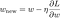
Substituamos o último termo da equação acima com o gradiente de L, L1 e L2 w.r.t.
L:

L1:

L2:

4) Como é evitado o excesso de equipamento?
Daqui em diante, vamos fazer as seguintes substituições nas equações acima (para melhor legibilidade):
- η = 1,
- H = 2x(wx+b-y)
que nos dão
L:

L1:
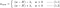
L2:
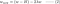
4.1) Com vs. Sem regularização
Observe as diferenças entre as atualizações de peso com o parâmetro de regularização λ e sem ele. Aqui estão algumas intuições.
Intuição A:
Dizemos com a Equação 0, calculando w-H dá-nos um valor w que leva ao sobreajustamento. Então, intuitivamente, as Equações {1.1, 1.2 e 2} irão reduzir as hipóteses de sobreajustamento porque a introdução de λ faz-nos afastar do mesmo w que nos iria causar problemas de sobreajustamento na frase anterior.
Intuição B:
Dizemos que um modelo sobreajustado significa que temos um valor w que é perfeito para o nosso modelo. ‘Perfeito’ significa que se substituirmos os dados (x) no modelo, nossa previsão ŷ será muito, muito próxima do verdadeiro y. Claro, é bom, mas nós não queremos perfeito. Porquê? Porque isto significa que o nosso modelo só se destina ao conjunto de dados no qual treinámos. Isto significa que o nosso modelo irá produzir previsões que estão muito longe do valor verdadeiro para outros conjuntos de dados. Então nos contentamos com menos do que perfeito, com a esperança de que nosso modelo também possa obter previsões próximas com outros dados. Para fazer isso, nós ‘manchamos’ esse w perfeito na Equação 0 com um termo de penalidade λ. Isso nos dá Equações {1.1, 1.2 e 2}.
Intuição C:
Notificação de que H (como definido aqui) depende do modelo (w e b) e dos dados (x e y). Actualizar os pesos com base apenas no modelo e nos dados da Equação 0 pode levar a sobreajustamentos, o que leva a uma fraca generalização. Por outro lado, nas Equações {1.1, 1.2 e 2}, o valor final de w não é influenciado apenas pelo modelo e dados, mas também por um parâmetro pré-definido λ que é independente do modelo e dados. Assim, podemos evitar o sobreajuste se definirmos um valor apropriado de λ, embora um valor demasiado grande faça com que o modelo seja severamente subajustado.
Intuição D:
Edden Gerber (obrigado!) forneceu uma intuição sobre a direcção para a qual a nossa solução está a ser deslocada. Dê uma olhada nos comentários: https://medium.com/@edden.gerber/thanks-for-the-article-1003ad7478b2
4.2) L1 vs. L2
Agora vamos focar a nossa atenção em L1 e L2, e reescrever as Equações {1.1, 1.2 e 2} reordenando seus termos λ e H da seguinte forma:
L1:
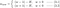
L2:
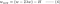
Comparar o segundo termo de cada uma das equações acima. Além de H, a mudança em w depende do termo ±λ ou do termo -2λw, que destacam a influência do seguinte:
- sign da corrente w (L1, L2)
- magnitude da corrente w (L2)
- doubling do parâmetro de regularização (L2)
Enquanto as atualizações de peso usando L1 são influenciadas pelo primeiro ponto, as atualizações de peso de L2 são influenciadas por todos os três pontos. Embora eu tenha feito esta comparação apenas com base na atualização da equação iterativa, note que isto não significa que uma é ‘melhor’ que a outra.
Por enquanto, vamos ver abaixo como um efeito de regularização de L1 pode ser alcançado apenas pelo sinal da corrente w.
4.3) Efeito de L1 em empurrar para 0 (sparsity)
Dê uma olhada em L1 na Equação 3.1. Se w for positivo, o parâmetro de regularização λ>0 irá empurrar w para ser menos positivo, subtraindo λ de w. Ao contrário na Equação 3.2, se w for negativo, λ será adicionado a w, empurrando-o para ser menos negativo. Portanto, isto tem o efeito de empurrar w para 0.
Isto é inútil num modelo de regressão linear de 1-variável, mas provará sua proeza para ‘remover’ variáveis inúteis em modelos de regressão multivariada. Você também pode pensar em L1 como reduzindo completamente o número de características no modelo. Aqui está um exemplo arbitrário de L1 tentando ‘empurrar’ algumas variáveis em um modelo de regressão linear multivariada:
Então como empurrar w para 0 ajuda na sobreposição na regularização de L1? Como mencionado acima, como w vai para 0, estamos reduzindo o número de características ao reduzir a importância da variável. Na equação acima, vemos que x_2, x_4 e x_5 são quase ‘inúteis’ por causa de seus pequenos coeficientes, portanto podemos removê-los da equação. Isto, por sua vez, reduz a complexidade do modelo, tornando o nosso modelo mais simples. Um modelo mais simples pode reduzir as hipóteses de sobreajustamento.
Nota
Embora L1 tenha a influência de empurrar os pesos para 0 e L2 não o faça, isto não implica que os pesos não sejam capazes de chegar perto de 0 devido a L2.
.
Deixe uma resposta