Elképzelések az L1 és L2 regularizációról

0) Mi az az L1 és L2?

A L1 és L2 regularizáció a nevét a w vektor L1 és L2 normájának köszönheti. Íme egy alapozó a normákról:

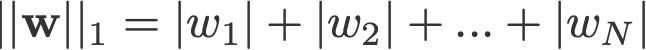
<változási log: kihagyta a 2-norm és a p-norm abszolút értékek felvételét>

Az L1 normát regularizációra megvalósító lineáris regressziós modellt lasso regressziónak, a (négyzetes) L2 normát regularizációra megvalósítót pedig ridge regressziónak nevezzük. E kettő megvalósításához vegyük észre, hogy a lineáris regressziós modell ugyanaz marad:

de a veszteségfüggvény számítása tartalmazza ezeket a regularizációs feltételeket:

.

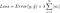
Megj: Szigorúan véve az utolsó egyenlet (ridge-regresszió) egy veszteségfüggvény a súlyok négyzetes L2 normájával (vegyük észre a négyzetgyök hiányát). (Köszönjük Max Pechyonkin-nak, hogy ezt kiemelte!)

A regularizációs kifejezések olyan “megkötések”, amelyekhez az optimalizáló algoritmusnak “ragaszkodnia” kell a veszteségfüggvény minimalizálásakor, azon kívül, hogy a valós y és a jósolt ŷ közötti hibát kell minimalizálnia.

1) Modell

Meghatározunk egy modellt, hogy lássuk, hogyan működik az L1 és az L2. Az egyszerűség kedvéért definiálunk egy egyszerű lineáris regressziós modellt ŷ egy független változóval.

Itt a mélytanulási konvenciókat w (‘weight’) és b (‘bias’) használtam.

A gyakorlatban az egyszerű lineáris regressziós modellek nem hajlamosak a túlillesztésre. Ahogy a bevezetőben említettük, a mélytanulási modellek a modell összetettsége miatt hajlamosabbak az ilyen problémákra.

Ezért vegyük figyelembe, hogy a cikkben használt kifejezések könnyen kiterjeszthetők összetettebb modellekre is, nem korlátozódva a lineáris regresszióra.

2) Veszteségfüggvények

Az L1 és L2 regularizáció hatásának bemutatására illesszük lineáris regressziós modellünket 3 különböző veszteségfüggvény/cél segítségével:

• L
• L1
• L2

A célunk az, hogy ezeket a különböző veszteségeket minimalizáljuk.

2.1) Veszteségfüggvény regularizáció nélkül

A veszteségfüggvényt L négyzetes hibaként definiáljuk, ahol a hiba az y (az igaz érték) és ŷ (az előre jelzett érték) közötti különbség.

Tegyük fel, hogy a modellünk túlillesztett lesz ezzel a veszteségfüggvénnyel.

2.2) Veszteségfüggvény L1 regularizációval

A fenti veszteségfüggvény alapján egy L1 regularizációs kifejezés hozzáadása a következőképpen néz ki:

ahol a regularizációs paraméter λ > 0 kézzel hangolható. Nevezzük ezt a veszteségfüggvényt L1-nek. Vegyük észre, hogy |w| mindenhol differenciálható, kivéve, ha w=0, mint az alábbiakban látható. Erre később szükségünk lesz.

2.3) Veszteségfüggvény L2 regularizációval

Hasonlóképpen, egy L2 regularizációs kifejezés hozzáadása L-hez így néz ki:

ahol ismét λ > 0.

3) Gradiens süllyedés

Most oldjuk meg a lineáris regressziós modellt gradiens süllyedéses optimalizálással a fent definiált 3 veszteségfüggvény alapján. Emlékezzünk vissza, hogy a w paraméter frissítése a gradiens ereszkedés során a következőképpen történik:

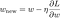
A fenti egyenlet utolsó tagját helyettesítsük az L, L1 és L2 gradiensével w függvényében.

L:

L1:

L2:

4) Hogyan akadályozzák meg a túlillesztést?

Végezzük el innentől kezdve a fenti egyenleteken a következő helyettesítéseket (a jobb olvashatóság érdekében):

• η = 1,
• H = 2x(wx+b-y)

amelyekből

L-t kapunk:

L1:

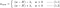
L2:

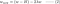
4.1) Regularizációval vs. regularizáció nélkül

Nézzük meg a különbségeket a λ regularizációs paraméterrel és anélkül végzett súlyfrissítések között. Íme néhány intuíció.

A intuíció:

Tegyük fel, hogy a 0. egyenlettel a w-H kiszámítása olyan w értéket ad, amely túlillesztéshez vezet. Akkor intuitív módon az {1.1, 1.2 és 2} egyenletek csökkentik a túlillesztés esélyét, mert λ bevezetésével éppen attól a w-től távolodunk el, ami az előző mondatban túlillesztési problémákat okozott volna.

Betét B:

Tegyük fel, hogy a túlillesztett modell azt jelenti, hogy olyan w értéket kapunk, ami tökéletes a modellünkhöz. A ‘tökéletes’ azt jelenti, hogy ha az adatokat (x) visszahelyeznénk a modellbe, a jóslatunk ŷ nagyon-nagyon közel lesz a valódi y-hoz. Persze, ez jó, de nem akarunk tökéleteset. Hogy miért? Mert ez azt jelenti, hogy a modellünk csak arra az adathalmazra való, amire betanítottuk. Ez azt jelenti, hogy a modellünk más adathalmazok esetében olyan előrejelzéseket fog produkálni, amelyek messze elmaradnak az igaz értéktől. Ezért megelégszünk a tökéletesnél kevésbé tökéletesekkel, abban a reményben, hogy a modellünk más adatokkal is közeli előrejelzéseket tud adni. Ehhez ezt a tökéletes w-t a 0. egyenletben egy λ büntetőtermmel “szennyezzük”. Így kapjuk meg az {1.1, 1.2 és 2} egyenleteket.

C intuíció:

Megjegyezzük, hogy az itt definiált H a modelltől (w és b) és az adatoktól (x és y) függ. A súlyok frissítése csak a 0. egyenletben szereplő modell és adatok alapján túlillesztéshez vezethet, ami gyenge általánosításhoz vezet. Másrészt az {1.1, 1.2 és 2} egyenletekben a w végső értékét nemcsak a modell és az adatok befolyásolják, hanem egy előre meghatározott λ paraméter is, amely független a modelltől és az adatoktól. Így megakadályozhatjuk a túlillesztést, ha megfelelő λ értéket állítunk be, bár a túl nagy érték a modell súlyos alulillesztését eredményezi.

Intuíció D:

Edden Gerber (köszönjük!) adott egy intuíciót arról, hogy milyen irányba tolódik el a megoldásunk. Nézd meg a hozzászólásokban: https://medium.com/@edden.gerber/thanks-for-the-article-1003ad7478b2

4.2) L1 vs. L2

Figyelmünket most L1-re és L2-re összpontosítjuk, és átírjuk az egyenleteket {1.1, 1.2 és 2} a λ- és H-tételeik átrendezésével a következőképpen:

L1:

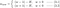
L2:

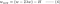
Vergessük össze a fenti egyenletek második tagját. H mellett a w változása a ±λ termtől vagy a -2λw termtől függ, amelyek a következők hatását emelik ki:

1. az aktuális w előjele (L1, L2)
2. az aktuális w nagysága (L2)
3. a regularizációs paraméter megduplázása (L2)

Míg az L1 segítségével történő súlyfrissítést az első pont befolyásolja, az L2-vel történő súlyfrissítést mindhárom pont befolyásolja. Bár ezt az összehasonlítást csak az iteratív egyenletfrissítés alapján végeztem, kérjük, vegye figyelembe, hogy ez nem jelenti azt, hogy az egyik “jobb”, mint a másik.

Előre nézzük meg az alábbiakban, hogyan érhető el az L1-ből származó regularizációs hatás pusztán az aktuális w előjelével.

4.3) Az L1 hatása a 0 felé való nyomásra (ritkaság)

Nézzük meg az L1-et a 3.1 egyenletben. Ha w pozitív, a λ>0 regularizációs paraméter λ>0 levonásával w-t kevésbé pozitívra tolja, levonva λ-t w-ből. Ezzel szemben a 3.2. egyenletben, ha w negatív, λ hozzáadódik w-hez, így azt kevésbé negatívra tolja. Ez tehát azt eredményezi, hogy w-t 0 felé tolja.

Ez természetesen értelmetlen egy 1 változós lineáris regressziós modellben, de bebizonyítja a hasznavehetetlen változók “eltávolítására” való alkalmasságát a többváltozós regressziós modellekben. Úgy is gondolhatunk az L1-re, mint a modellben lévő jellemzők számának teljes csökkentésére. Íme egy tetszőleges példa arra, hogy az L1 megpróbál néhány változót “eltolni” egy többváltozós lineáris regressziós modellben:

Hogyan segít a w 0 felé tolása a túlillesztésben az L1 regularizációban? Ahogy fentebb említettük, ahogy w 0 felé megy, a változók fontosságának csökkentésével csökkentjük a jellemzők számát. A fenti egyenletben azt látjuk, hogy az x_2, x_4 és x_5 kis együtthatóik miatt szinte “haszontalanok”, ezért eltávolíthatjuk őket az egyenletből. Ez viszont csökkenti a modell bonyolultságát, így a modellünk egyszerűbbé válik. Egy egyszerűbb modell csökkentheti a túlillesztés esélyét.

Megjegyzés

Míg az L1 hatására a súlyok 0 felé tolódnak, az L2 nem, ez nem jelenti azt, hogy a súlyok az L2 miatt nem képesek 0 közelébe kerülni.