Intuitions sur la régularisation L1 et L2

0) C’est quoi L1 et L2 ?

La régularisation L1 et L2 doit son nom à la norme L1 et L2 d’un vecteur w respectivement. Voici un abécédaire des normes :

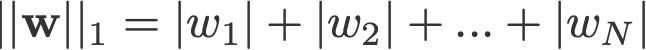
<changement de log : omis de prendre les absolus pour 2-norm et p-norm>

Un modèle de régression linéaire qui met en œuvre la norme L1 pour la régularisation est appelé régression lasso, et celui qui met en œuvre la norme (au carré) L2 pour la régularisation est appelé régression ridge. Pour mettre en œuvre ces deux, notez que le modèle de régression linéaire reste le même :

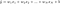
mais c’est le calcul de la fonction de perte qui inclut ces termes de régularisation :

.

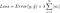
Note : Strictement parlant, la dernière équation (régression ridge) est une fonction de perte avec régularisation L2 des poids (remarquez l’absence de la racine carrée). (Merci à Max Pechyonkin d’avoir mis cela en évidence !)

Les termes de régularisation sont des « contraintes » auxquelles un algorithme d’optimisation doit « adhérer » lorsqu’il minimise la fonction de perte, en dehors du fait qu’il doit minimiser l’erreur entre le vrai y et le prédit ŷ.

1) Modèle

Définissons un modèle pour voir comment fonctionnent L1 et L2. Pour simplifier, nous définissons un modèle de régression linéaire simple ŷ avec une variable indépendante.

J’ai utilisé ici les conventions de deep learning w (‘weight’) et b (‘bias’).

En pratique, les modèles de régression linéaire simples ne sont pas enclins à l’overfitting. Comme mentionné dans l’introduction, les modèles d’apprentissage profond sont plus sensibles à de tels problèmes en raison de la complexité de leur modèle.

A ce titre, notez que les expressions utilisées dans cet article sont facilement étendues à des modèles plus complexes, sans se limiter à la régression linéaire.

2) Fonctions de perte

Pour démontrer l’effet de la régularisation L1 et L2, ajustons notre modèle de régression linéaire en utilisant 3 fonctions de perte/objectifs différents :

• L
• L1
• L2

Notre objectif est de minimiser ces différentes pertes.

2.1) Fonction de perte sans régularisation

Nous définissons la fonction de perte L comme l’erreur au carré, où l’erreur est la différence entre y (la valeur réelle) et ŷ (la valeur prédite).

Supposons que notre modèle sera surajusté en utilisant cette fonction de perte.

2.2) Fonction de perte avec régularisation L1

Sur la base de la fonction de perte ci-dessus, y ajouter un terme de régularisation L1 ressemble à ceci :

où le paramètre de régularisation λ > 0 est réglé manuellement. Appelons cette fonction de perte L1. Notez que |w| est différentiable partout sauf lorsque w=0, comme indiqué ci-dessous. Nous en aurons besoin plus tard.

2.3) Fonction de perte avec régularisation L2

De manière similaire, ajouter un terme de régularisation L2 à L ressemble à ceci :

où encore une fois, λ > 0.

3) Descente de gradient

Maintenant, résolvons le modèle de régression linéaire en utilisant l’optimisation par descente de gradient basée sur les 3 fonctions de perte définies ci-dessus. Rappelons que la mise à jour du paramètre w en descente de gradient est la suivante :

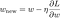
Substituons le dernier terme de l’équation ci-dessus par le gradient de L, L1 et L2 w.r.t. w.

L:

L1 :

L2 :

4) Comment empêche-t-on le surajustement ?

À partir de là, effectuons les substitutions suivantes sur les équations ci-dessus (pour une meilleure lisibilité) :

• η = 1,
• H = 2x(wx+b-y)

ce qui nous donne

L :

L1:

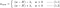
L2 :

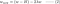
4.1) Avec vs sans régularisation

Observez les différences entre les mises à jour des poids avec le paramètre de régularisation λ et sans celui-ci. Voici quelques intuitions.

Intuition A:

Disons qu’avec l’équation 0, le calcul de w-H nous donne une valeur de w qui conduit à un surajustement. Alors, intuitivement, les équations {1.1, 1.2 et 2} réduiront les chances de surajustement parce que l’introduction de λ nous fait nous éloigner de la valeur w même qui allait nous causer des problèmes de surajustement dans la phrase précédente.

Intuition B:

Disons qu’un modèle surajusté signifie que nous avons une valeur w qui est parfaite pour notre modèle. ‘Parfait’ signifie que si nous substituions les données (x) à nouveau dans le modèle, notre prédiction ŷ sera très, très proche du vrai y. Bien sûr, c’est bien, mais nous ne voulons pas du parfait. Pourquoi ? Parce que cela signifie que notre modèle n’est destiné qu’à l’ensemble de données sur lequel nous nous sommes entraînés. Cela signifie que notre modèle produira des prédictions très éloignées de la valeur réelle pour d’autres ensembles de données. Nous nous contentons donc d’un modèle moins que parfait, en espérant qu’il pourra également obtenir des prédictions proches avec d’autres données. Pour ce faire, nous « entachons » ce w parfait dans l’équation 0 avec un terme de pénalité λ. Cela nous donne les équations {1.1, 1.2 et 2}.

Intuition C:

Notez que H (tel que défini ici) dépend du modèle (w et b) et des données (x et y). La mise à jour des poids basée uniquement sur le modèle et les données dans l’équation 0 peut conduire à un surajustement, ce qui entraîne une mauvaise généralisation. En revanche, dans les équations {1.1, 1.2 et 2}, la valeur finale de w n’est pas seulement influencée par le modèle et les données, mais aussi par un paramètre prédéfini λ qui est indépendant du modèle et des données. Ainsi, nous pouvons éviter l’overfitting si nous définissons une valeur appropriée de λ, bien qu’une valeur trop grande entraînera un sévère underfit du modèle.

Intuition D:

Edden Gerber (merci !) a fourni une intuition sur la direction vers laquelle notre solution est déplacée. Jetez-y un coup d’œil dans les commentaires : https://medium.com/@edden.gerber/thanks-for-the-article-1003ad7478b2

4.2) L1 vs. L2

Nous allons maintenant concentrer notre attention sur L1 et L2, et réécrire les équations {1.1, 1.2 et 2} en réarrangeant leurs termes λ et H comme suit :

L1:

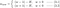
L2 :

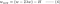
Comparer le second terme de chacune des équations ci-dessus. En dehors de H, le changement de w dépend du terme ±λ ou du terme -2λw, qui mettent en évidence l’influence des éléments suivants :

1. signe du w actuel (L1, L2)
2. magnitude du w actuel (L2)
3. doublement du paramètre de régularisation (L2)

Alors que les mises à jour de poids utilisant L1 sont influencées par le premier point, les mises à jour de poids provenant de L2 sont influencées par les trois points. Bien que j’aie fait cette comparaison juste sur la base de la mise à jour itérative de l’équation, veuillez noter que cela ne signifie pas que l’une est « meilleure » que l’autre.

Pour l’instant, voyons ci-dessous comment un effet de régularisation de L1 peut être atteint juste par le signe du w actuel.

4.3) Effet de L1 sur la poussée vers 0 (sparsité)

Regardez L1 dans l’équation 3.1. Si w est positif, le paramètre de régularisation λ>0 poussera w à être moins positif, en soustrayant λ de w. Inversement, dans l’équation 3.2, si w est négatif, λ sera ajouté à w, le poussant à être moins négatif. Par conséquent, cela a pour effet de pousser w vers 0.

Ceci est bien sûr inutile dans un modèle de régression linéaire à 1 variable, mais prouvera ses prouesses pour  » supprimer  » les variables inutiles dans les modèles de régression multivariés. Vous pouvez également considérer que L1 réduit le nombre de caractéristiques dans le modèle. Voici un exemple arbitraire de L1 essayant de ‘pousser’ certaines variables dans un modèle de régression linéaire multivarié :

Alors, comment le fait de pousser w vers 0 aide-t-il au surajustement dans la régularisation L1 ? Comme mentionné plus haut, lorsque w va vers 0, nous réduisons le nombre de caractéristiques en réduisant l’importance de la variable. Dans l’équation ci-dessus, nous voyons que x_2, x_4 et x_5 sont presque  » inutiles  » en raison de leurs petits coefficients, nous pouvons donc les supprimer de l’équation. Cela réduit à son tour la complexité du modèle, ce qui rend notre modèle plus simple. Un modèle plus simple peut réduire les chances d’overfitting.

Note

Alors que L1 a l’influence de pousser les poids vers 0 et que L2 ne l’a pas, cela n’implique pas que les poids ne puissent pas atteindre près de 0 à cause de L2.