Intuiciones sobre la regularización L1 y L2

0) ¿Qué es L1 y L2?

La regularización L1 y L2 debe su nombre a la norma L1 y L2 de un vector w respectivamente. Aquí tienes una introducción a las normas:

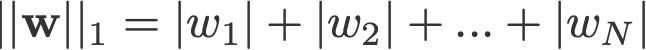
<cambio de registro: omitió tomar los absolutos para la norma 2 y la norma p>

Un modelo de regresión lineal que implementa la norma L1 para la regularización se llama regresión del lazo, y uno que implementa la norma L2 (al cuadrado) para la regularización se llama regresión de la cresta. Para implementar estos dos, observe que el modelo de regresión lineal sigue siendo el mismo:

pero es el cálculo de la función de pérdida el que incluye estos términos de regularización:

.

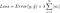
Nota: Estrictamente hablando, la última ecuación (regresión ridge) es una función de pérdida con norma L2 cuadrada de los pesos (nótese la ausencia de la raíz cuadrada). (¡Gracias a Max Pechyonkin por resaltar esto!)

Los términos de regularización son «restricciones» a las que un algoritmo de optimización debe «adherirse» al minimizar la función de pérdida, aparte de tener que minimizar el error entre el verdadero y y el predicho ŷ.

1) Modelo

Definamos un modelo para ver cómo funcionan L1 y L2. Para simplificar, definimos un modelo de regresión lineal simple ŷ con una variable independiente.

Aquí he utilizado las convenciones de aprendizaje profundo w (‘peso’) y b (‘sesgo’).

En la práctica, los modelos de regresión lineal simples no son propensos al sobreajuste. Como se mencionó en la introducción, los modelos de aprendizaje profundo son más susceptibles a tales problemas debido a la complejidad de su modelo.

Como tal, tenga en cuenta que las expresiones utilizadas en este artículo se extienden fácilmente a los modelos más complejos, no se limita a la regresión lineal.

2) Funciones de pérdida

Para demostrar el efecto de la regularización L1 y L2, vamos a ajustar nuestro modelo de regresión lineal utilizando 3 funciones de pérdida/objetivos diferentes:

• L
• L1
• L2

Nuestro objetivo es minimizar estas diferentes pérdidas.

2.1) Función de pérdida sin regularización

Definimos la función de pérdida L como el error al cuadrado, donde el error es la diferencia entre y (el valor verdadero) y ŷ (el valor predicho).

Supongamos que nuestro modelo estará sobreajustado utilizando esta función de pérdida.

2.2) Función de pérdida con regularización L1

Basado en la función de pérdida anterior, añadirle un término de regularización L1 tiene el siguiente aspecto:

donde el parámetro de regularización λ > 0 se ajusta manualmente. Llamemos a esta función de pérdida L1. Tenga en cuenta que |w| es diferenciable en todas partes excepto cuando w=0, como se muestra a continuación. Lo necesitaremos más adelante.

2.3) Función de pérdida con regularización L2

De forma similar, añadiendo un término de regularización L2 a L queda así:

donde de nuevo, λ > 0.

3) Descenso de gradiente

Ahora, resolvamos el modelo de regresión lineal utilizando la optimización de descenso de gradiente basada en las 3 funciones de pérdida definidas anteriormente. Recordemos que la actualización del parámetro w en el descenso de gradiente es la siguiente:

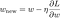
Sustituyamos el último término de la ecuación anterior por el gradiente de L, L1 y L2 con respecto a w.

L:

L1:

L2:

4) ¿Cómo se evita el sobreajuste?

A partir de aquí, vamos a realizar las siguientes sustituciones en las ecuaciones anteriores (para una mejor legibilidad):

• η = 1,
• H = 2x(wx+b-y)

que nos dan

L:

L1:

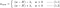
L2:

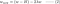
4.1) Con vs. Sin Regularización

Observe las diferencias entre las actualizaciones de pesos con el parámetro de regularización λ y sin él. He aquí algunas intuiciones.

Intuición A:

Digamos que con la Ecuación 0, el cálculo de w-H nos da un valor de w que conduce al sobreajuste. Entonces, intuitivamente, las ecuaciones {1.1, 1.2 y 2} reducirán las posibilidades de sobreajuste porque la introducción de λ hace que nos alejemos de la propia w que nos iba a causar problemas de sobreajuste en la frase anterior.

Intuición B:

Digamos que un modelo sobreajustado significa que tenemos un valor de w que es perfecto para nuestro modelo. ‘Perfecto’ significa que si volvemos a sustituir los datos (x) en el modelo, nuestra predicción ŷ estará muy, muy cerca de la verdadera y. Claro, es bueno, pero no queremos que sea perfecto. ¿Por qué? Porque esto significa que nuestro modelo sólo está pensado para el conjunto de datos en el que nos hemos entrenado. Esto significa que nuestro modelo producirá predicciones que están muy lejos del valor real para otros conjuntos de datos. Así que nos conformamos con algo menos que perfecto, con la esperanza de que nuestro modelo también pueda obtener predicciones cercanas con otros datos. Para ello, «manchamos» esta w perfecta en la ecuación 0 con un término de penalización λ. Esto nos da las ecuaciones {1.1, 1.2 y 2}.

Intuición C:

Nótese que H (como se define aquí) depende del modelo (w y b) y de los datos (x e y). Actualizar las ponderaciones basándose sólo en el modelo y los datos en la ecuación 0 puede llevar a un sobreajuste, lo que conduce a una mala generalización. Por otro lado, en las ecuaciones {1.1, 1.2 y 2}, el valor final de w no sólo está influenciado por el modelo y los datos, sino también por un parámetro predefinido λ que es independiente del modelo y los datos. Así, podemos evitar el sobreajuste si fijamos un valor adecuado de λ, aunque un valor demasiado grande hará que el modelo esté gravemente infraajustado.

Intuición D:

Edden Gerber (¡gracias!) ha proporcionado una intuición sobre la dirección hacia la que se desplaza nuestra solución. Échale un vistazo en los comentarios: https://medium.com/@edden.gerber/thanks-for-the-article-1003ad7478b2

4.2) L1 frente a L2

Ahora centraremos nuestra atención en L1 y L2, y reescribiremos las ecuaciones {1.1, 1.2 y 2} reordenando sus términos λ y H como sigue:

L1:

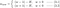
L2:

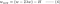
Compare el segundo término de cada una de las ecuaciones anteriores. Aparte de H, el cambio en w depende del término ±λ o del término -2λw, que ponen de manifiesto la influencia de lo siguiente:

1. signo de la corriente w (L1, L2)
2. magnitud de la corriente w (L2)
3. duplicación del parámetro de regularización (L2)

Mientras que las actualizaciones de peso que utilizan L1 están influidas por el primer punto, las actualizaciones de peso de L2 están influidas por los tres puntos. Mientras que he hecho esta comparación sólo sobre la base de la actualización de la ecuación iterativa, tenga en cuenta que esto no significa que uno es «mejor» que el otro.

Por ahora, vamos a ver a continuación cómo un efecto de regularización de L1 se puede lograr sólo por el signo de la actual w.

4.3) El efecto de L1 en empujar hacia 0 (sparsity)

Echa un vistazo a L1 en la ecuación 3.1. Si w es positivo, el parámetro de regularización λ>0 empujará a w a ser menos positivo, restando λ de w. A la inversa, en la ecuación 3.2, si w es negativo, λ se añadirá a w, empujándolo a ser menos negativo. Por lo tanto, esto tiene el efecto de empujar w hacia 0.

Esto es, por supuesto, inútil en un modelo de regresión lineal de 1 variable, pero demostrará su destreza para «eliminar» variables inútiles en los modelos de regresión multivariante. También se puede pensar en L1 como la reducción del número de características en el modelo por completo. He aquí un ejemplo arbitrario de L1 tratando de «empujar» algunas variables en un modelo de regresión lineal multivariante:

Entonces, ¿cómo ayuda empujar w hacia 0 en el sobreajuste en la regularización L1? Como se mencionó anteriormente, a medida que w va a 0, estamos reduciendo el número de características mediante la reducción de la importancia de la variable. En la ecuación anterior, vemos que x_2, x_4 y x_5 son casi «inútiles» debido a sus pequeños coeficientes, por lo que podemos eliminarlos de la ecuación. Esto, a su vez, reduce la complejidad del modelo, haciéndolo más sencillo. Un modelo más simple puede reducir las posibilidades de sobreajuste.

Nota

Aunque L1 tiene la influencia de empujar los pesos hacia 0 y L2 no, esto no implica que los pesos no puedan llegar cerca de 0 debido a L2.