Einführungen zur L1- und L2-Regularisierung

0) Was ist L1 und L2?

L1- und L2-Regularisierung verdanken ihren Namen der L1- bzw. L2-Norm eines Vektors w. Hier ist eine Einführung in die Normierung:

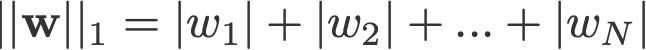
<Änderungslog: Auslassen der Absolutwerte für 2-Norm und p-Norm>

Ein lineares Regressionsmodell, das die L1-Norm für die Regularisierung einsetzt, wird Lassoregression genannt, und eines, das die (quadrierte) L2-Norm für die Regularisierung einsetzt, heißt Ridge-Regression. Um diese beiden Modelle zu implementieren, ist zu beachten, dass das lineare Regressionsmodell dasselbe bleibt:

aber die Berechnung der Verlustfunktion beinhaltet diese Regularisierungsterme:

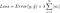
Anmerkung: Streng genommen handelt es sich bei der letzten Gleichung (Ridge-Regression) um eine Verlustfunktion mit quadrierter L2-Norm der Gewichte (man beachte das Fehlen der Quadratwurzel). (Vielen Dank an Max Pechyonkin für den Hinweis!)

Die Regularisierungsterme sind „Beschränkungen“, die ein Optimierungsalgorithmus bei der Minimierung der Verlustfunktion „einhalten“ muss, abgesehen davon, dass er den Fehler zwischen dem wahren y und dem vorhergesagten ŷ minimieren muss.

1) Modell

Lassen Sie uns ein Modell definieren, um zu sehen, wie L1 und L2 funktionieren. Der Einfachheit halber definieren wir ein einfaches lineares Regressionsmodell ŷ mit einer unabhängigen Variable.

Hier habe ich die Deep-Learning-Konventionen w („Gewicht“) und b („Bias“) verwendet.

In der Praxis sind einfache lineare Regressionsmodelle nicht anfällig für Overfitting. Wie in der Einleitung erwähnt, sind Deep-Learning-Modelle aufgrund ihrer Modellkomplexität anfälliger für solche Probleme.

Daher ist zu beachten, dass die in diesem Artikel verwendeten Ausdrücke leicht auf komplexere Modelle erweitert werden können, die nicht auf lineare Regression beschränkt sind.

2) Verlustfunktionen

Um die Wirkung der L1- und L2-Regularisierung zu demonstrieren, passen wir unser lineares Regressionsmodell mit 3 verschiedenen Verlustfunktionen/Zielen an:

• L
• L1
• L2

Unser Ziel ist es, diese verschiedenen Verluste zu minimieren.

2.1) Verlustfunktion ohne Regularisierung

Wir definieren die Verlustfunktion L als den quadrierten Fehler, wobei Fehler die Differenz zwischen y (dem wahren Wert) und ŷ (dem vorhergesagten Wert) ist.

Nehmen wir an, dass unser Modell mit dieser Verlustfunktion übererfüllt wird.

2.2) Verlustfunktion mit L1-Regularisierung

Ausgehend von der obigen Verlustfunktion sieht das Hinzufügen eines L1-Regularisierungsterms wie folgt aus:

wobei der Regularisierungsparameter λ > 0 manuell eingestellt wird. Nennen wir diese Verlustfunktion L1. Beachten Sie, dass |w| überall differenzierbar ist, außer wenn w=0, wie unten gezeigt. Wir werden dies später brauchen.

2.3) Verlustfunktion mit L2-Regularisierung

Ähnlich sieht es aus, wenn man einen L2-Regularisierungsterm zu L hinzufügt:

wobei wiederum λ > 0 ist.

3) Gradientenabstieg

Lösen wir nun das lineare Regressionsmodell mit Hilfe der Gradientenabstiegsoptimierung auf der Grundlage der drei oben definierten Verlustfunktionen. Erinnern wir uns daran, dass die Aktualisierung des Parameters w beim Gradientenabstieg wie folgt abläuft:

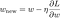
Ersetzen wir den letzten Term in der obigen Gleichung mit dem Gradienten von L, L1 und L2 w.r.t. w.

L:

L1:

L2:

4) Wie wird Overfitting verhindert?

Führen wir von hier an die folgenden Substitutionen an den obigen Gleichungen durch (zur besseren Lesbarkeit):

• η = 1,
• H = 2x(wx+b-y)

was uns

L liefert:

L1:

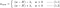
L2:

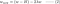
4.1) Mit vs. ohne Regularisierung

Betrachten Sie die Unterschiede zwischen den Gewichtsaktualisierungen mit und ohne Regularisierungsparameter λ. Hier sind einige Intuitionen:

Intuition A:

Angenommen, die Berechnung von w-H mit Gleichung 0 ergibt einen w-Wert, der zu einer Überanpassung führt. Dann werden die Gleichungen {1.1, 1.2 und 2} intuitiv die Wahrscheinlichkeit einer Überanpassung verringern, weil wir durch die Einführung von λ von dem w-Wert wegkommen, der uns im vorherigen Satz Probleme mit der Überanpassung bereitet hat.

Intuition B:

Angenommen, ein überangepasstes Modell bedeutet, dass wir einen w-Wert haben, der für unser Modell perfekt ist. ‚Perfekt‘ bedeutet, dass, wenn wir die Daten (x) wieder in das Modell einsetzen, unsere Vorhersage ŷ sehr, sehr nahe am wahren y liegen wird. Warum? Weil das bedeutet, dass unser Modell nur für den Datensatz geeignet ist, auf dem wir trainiert haben. Das bedeutet, dass unser Modell für andere Datensätze Vorhersagen produzieren wird, die weit vom wahren Wert entfernt sind. Wir geben uns also mit weniger als perfekt zufrieden, in der Hoffnung, dass unser Modell auch mit anderen Daten gute Vorhersagen machen kann. Um dies zu erreichen, „färben“ wir dieses perfekte w in Gleichung 0 mit einem Strafterm λ. So erhalten wir die Gleichungen {1.1, 1.2 und 2}.

Vermutung C:

Beachte, dass H (wie hier definiert) vom Modell (w und b) und den Daten (x und y) abhängt. Die Aktualisierung der Gewichte nur auf der Grundlage des Modells und der Daten in Gleichung 0 kann zu einer Überanpassung führen, die eine schlechte Generalisierung zur Folge hat. In den Gleichungen {1.1, 1.2 und 2} hingegen wird der endgültige Wert von w nicht nur durch das Modell und die Daten beeinflusst, sondern auch durch einen vordefinierten Parameter λ, der vom Modell und den Daten unabhängig ist. So können wir eine Überanpassung verhindern, wenn wir einen geeigneten Wert für λ festlegen, obwohl ein zu großer Wert zu einer starken Unteranpassung des Modells führt.

Intuition D:

Edden Gerber (danke!) hat eine Intuition über die Richtung geliefert, in die unsere Lösung verschoben wird. Werfen Sie einen Blick in die Kommentare: https://medium.com/@edden.gerber/thanks-for-the-article-1003ad7478b2

4.2) L1 vs. L2

Wir werden nun unsere Aufmerksamkeit auf L1 und L2 richten und die Gleichungen {1.1, 1.2 und 2}, indem wir ihre λ- und H-Terme wie folgt umschreiben:

L1:

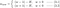
L2:

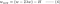
Vergleiche den zweiten Term jeder der obigen Gleichungen. Abgesehen von H hängt die Änderung von w vom ±λ-Term oder dem -2λw-Term ab, was den Einfluss der folgenden Punkte hervorhebt:

1. Vorzeichen des aktuellen w (L1, L2)
2. Größe des aktuellen w (L2)
3. Verdoppelung des Regularisierungsparameters (L2)

Während Gewichtsaktualisierungen mit L1 vom ersten Punkt beeinflusst werden, werden Gewichtsaktualisierungen von L2 von allen drei Punkten beeinflusst. Obwohl ich diesen Vergleich nur auf der Grundlage der iterativen Gleichungsaktualisierung durchgeführt habe, bedeutet dies nicht, dass die eine „besser“ ist als die andere.

Wir wollen im Folgenden sehen, wie ein Regularisierungseffekt von L1 allein durch das Vorzeichen des aktuellen w erreicht werden kann.

4.3) L1’s effect on pushing towards 0 (sparsity)

Betrachten Sie L1 in Gleichung 3.1. Wenn w positiv ist, wird der Regularisierungsparameter λ>0 dazu führen, dass w weniger positiv ist, indem λ von w subtrahiert wird. Umgekehrt wird in Gleichung 3.2, wenn w negativ ist, λ zu w addiert, so dass es weniger negativ ist. Dadurch wird w gegen 0 gedrückt.

Dies ist natürlich in einem linearen 1-Variablen-Regressionsmodell sinnlos, wird sich aber bei multivariaten Regressionsmodellen als nützlich erweisen, um nutzlose Variablen zu „entfernen“. Man kann sich L1 auch so vorstellen, dass es die Anzahl der Merkmale im Modell insgesamt reduziert. Hier ist ein willkürliches Beispiel dafür, wie L1 versucht, einige Variablen in einem multivariaten linearen Regressionsmodell zu „verdrängen“:

Wie hilft also das Verdrängen von w gegen 0 bei der L1-Regularisierung beim Overfitting? Wie bereits erwähnt, verringert sich die Anzahl der Merkmale, wenn w gegen 0 geht, indem die Bedeutung der Variablen reduziert wird. In der obigen Gleichung sehen wir, dass x_2, x_4 und x_5 aufgrund ihrer kleinen Koeffizienten fast „nutzlos“ sind, weshalb wir sie aus der Gleichung entfernen können. Dies wiederum verringert die Komplexität des Modells und macht unser Modell einfacher. Ein einfacheres Modell kann das Risiko einer Überanpassung verringern.

Hinweis

Obwohl L1 einen Einfluss darauf hat, die Gewichte gegen 0 zu drücken, und L2 nicht, bedeutet dies nicht, dass die Gewichte aufgrund von L2 nicht nahe an 0 heranreichen können.