Intuitioner om L1- og L2-regularisering
On september 20, 2021 by admin0) Hvad er L1 og L2?
L1- og L2-regularisering har sit navn efter henholdsvis L1- og L2-norm for en vektor w. Her er en grundbog om normer:
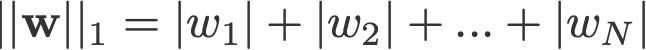


<ændre log: glemte at tage absolutte værdier for 2-norm og p-norm>
En lineær regressionsmodel, der implementerer L1-norm til regularisering, kaldes lasso-regression, og en model, der implementerer (kvadreret) L2-norm til regularisering, kaldes ridge-regression. For at implementere disse to skal man bemærke, at den lineære regressionsmodel forbliver den samme:
men det er beregningen af tabsfunktionen, der omfatter disse regulariseringstermer:

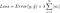

Note: Strengt taget er den sidste ligning (ridge-regression) en tabsfunktion med en kvadreret L2-norm for vægtene (bemærk fraværet af kvadratroden). (Tak til Max Pechyonkin for at fremhæve dette!)
Regulariseringstermerne er “begrænsninger”, som en optimeringsalgoritme skal “overholde”, når den minimerer tabsfunktionen, bortset fra at den skal minimere fejlen mellem det sande y og det forudsagte ŷ.
1) Model
Lad os definere en model for at se, hvordan L1 og L2 fungerer. For enkelhedens skyld definerer vi en simpel lineær regressionsmodel ŷ med én uafhængig variabel.
Her har jeg anvendt deep learning-konventionerne w (‘weight’) og b (‘bias’).
I praksis er simple lineære regressionsmodeller ikke tilbøjelige til at blive overfittet. Som nævnt i indledningen er deep learning-modeller mere modtagelige for sådanne problemer på grund af deres modelkompleksitet.
Som sådan skal du bemærke, at de udtryk, der anvendes i denne artikel, let kan udvides til mere komplekse modeller, der ikke er begrænset til lineær regression.
2) Tabsfunktioner
For at demonstrere effekten af L1- og L2-regularisering skal vi tilpasse vores lineære regressionsmodel ved hjælp af 3 forskellige tabsfunktioner/målsætninger:
- L
- L1
- L2
Vores mål er at minimere disse forskellige tab.
2.1) Tabsfunktion uden regularisering
Vi definerer tabsfunktionen L som den kvadrerede fejl, hvor fejl er forskellen mellem y (den sande værdi) og ŷ (den forudsagte værdi).

Lad os antage, at vores model vil blive overfittet ved hjælp af denne tabsfunktion.
2.2) Tabsfunktion med L1-regularisering
Baseret på ovenstående tabsfunktion ser tilføjelse af et L1-regulariseringsterm til den således ud:

hvor regulariseringsparameteren λ > 0 indstilles manuelt. Lad os kalde denne tabsfunktion L1. Bemærk, at |w| er differentiabel overalt, undtagen når w=0, som vist nedenfor. Det får vi brug for senere.

2.3) Tabsfunktion med L2-regularisering
Sådan ser det ud, hvis man tilføjer et L2-regulariseringsterm til L:

hvor igen λ > 0.
3) Gradient Descent
Nu skal vi løse den lineære regressionsmodel ved hjælp af gradient descent-optimering baseret på de 3 tabsfunktioner, der er defineret ovenfor. Husk, at opdatering af parameteren w i gradient descent er som følger:
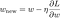
Lad os erstatte det sidste udtryk i ovenstående ligning med gradienten for L, L1 og L2 w.r.t. w.
L:

L1:

L2:

4) Hvordan forhindres overfitting?
Fra og med dette punkt udfører vi følgende substitutioner på ovenstående ligninger (for bedre læsbarhed):
- η = 1,
- H = 2x(wx+b-y)
hvilket giver os
L:

L1:
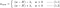
L2:
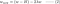
4.1) Med vs. uden regularisering
Opmærksomheden henledes på forskellene mellem vægtopdateringerne med regulariseringsparameteren λ og uden den. Her er nogle intuitioner.
Intuition A:
Lad os sige med ligning 0, at beregning af w-H giver os en w-værdi, der fører til overpasning. Så vil ligningerne {1.1, 1.2 og 2} intuitivt set reducere chancerne for overfitting, fordi indførelsen af λ får os til at flytte os væk fra netop den w-værdi, der ville give os problemer med overfitting i den foregående sætning.
Intuition B:
Lad os sige, at en overfittet model betyder, at vi har en w-værdi, der er perfekt for vores model. ‘Perfekt’ betyder, at hvis vi erstattede dataene (x) tilbage i modellen, vil vores forudsigelse ŷ være meget, meget tæt på den sande y. Selvfølgelig er det godt, men vi vil ikke have perfekt. Hvorfor? Fordi det betyder, at vores model kun er beregnet til det datasæt, som vi har trænet på. Det betyder, at vores model vil producere forudsigelser, der ligger langt fra den sande værdi for andre datasæt. Så vi nøjes med mindre end perfekt med håbet om, at vores model også kan få tætte forudsigelser med andre data. For at gøre dette “taint” vi denne perfekte w i ligning 0 med et strafudtryk λ. Dette giver os ligningerne {1.1, 1.2 og 2}.
Intuition C:
Bemærk, at H (som defineret her) er afhængig af modellen (w og b) og dataene (x og y). Hvis vægtene opdateres udelukkende på grundlag af modellen og dataene i ligning 0, kan det føre til overtilpasning, hvilket fører til dårlig generalisering. På den anden side er den endelige værdi af w i ligningerne {1.1, 1.2 og 2} ikke kun påvirket af modellen og dataene, men også af en foruddefineret parameter λ, som er uafhængig af modellen og dataene. Vi kan således forhindre overfitting, hvis vi indstiller en passende værdi af λ, selv om en for stor værdi vil medføre, at modellen bliver alvorligt underfittet.
Intuition D:
Edden Gerber (tak!) har givet en intuition om den retning, som vores løsning bliver forskudt i. Tag et kig i kommentarerne: https://medium.com/@edden.gerber/thanks-for-the-article-1003ad7478b2
4.2) L1 vs. L2
Vi skal nu rette vores opmærksomhed mod L1 og L2 og omskrive ligningerne {1.1, 1.2 og 2} ved at omarrangere deres λ- og H-termer som følger:
L1:
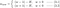
L2:
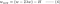
Sammenlign det andet udtryk i hver af ligningerne ovenfor. Ud over H afhænger ændringen i w af ±λ-terminen eller -2λw-terminen, hvilket fremhæver indflydelsen af følgende:
- tegnet på nuværende w (L1, L2)
- størrelsen af nuværende w (L2)
- fordobling af regulariseringsparameteren (L2)
Mens vægtopdateringer ved hjælp af L1 påvirkes af det første punkt, påvirkes vægtopdateringer fra L2 af alle de tre punkter. Selv om jeg har foretaget denne sammenligning udelukkende på baggrund af den iterative ligningsopdatering, skal du være opmærksom på, at det ikke betyder, at den ene er “bedre” end den anden.
For nu ser vi nedenfor, hvordan en regulariseringseffekt fra L1 kan opnås alene ved fortegnet på den aktuelle w.
4.3) L1’s effekt på at skubbe mod 0 (sparsomhed)
Tag et kig på L1 i ligning 3.1. Hvis w er positiv, vil regulariseringsparameteren λ>0 skubbe w til at være mindre positiv, ved at trække λ fra w. Omvendt i ligning 3.2, hvis w er negativ, vil λ blive tilføjet til w, hvilket skubber den til at være mindre negativ. Dette har således den virkning, at w skubbes mod 0.
Dette er naturligvis meningsløst i en lineær regressionsmodel med én variabel, men vil vise sig at være en god idé til at “fjerne” ubrugelige variabler i multivariate regressionsmodeller. Du kan også tænke på L1 som en reduktion af antallet af funktioner i modellen i det hele taget. Her er et vilkårligt eksempel på, at L1 forsøger at ‘skubbe’ nogle variabler i en multivariat lineær regressionsmodel:
Så hvordan hjælper det at skubbe w mod 0 med at overfitte i L1-regularisering? Som nævnt ovenfor reducerer vi antallet af funktioner, når w går mod 0, ved at reducere variablernes betydning. I ligningen ovenfor kan vi se, at x_2, x_4 og x_5 er næsten “ubrugelige” på grund af deres små koefficienter, og derfor kan vi fjerne dem fra ligningen. Dette reducerer igen modellens kompleksitet, hvilket gør vores model enklere. En enklere model kan mindske risikoen for overfitting.
Note
Mens L1 har indflydelse på at skubbe vægtene mod 0, og L2 ikke har det, betyder det ikke, at vægtene ikke kan nå tæt på 0 på grund af L2.
Skriv et svar