Intuice o L1 a L2 regularizaci

0) Co je to L1 a L2?

L1 a L2 regularizace vděčí za svůj název normě L1, respektive L2 vektoru w. Zde je základní informace o normách:

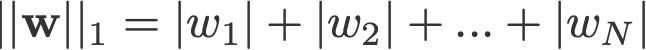
<změna log: vynecháno převzetí absolutních hodnot pro 2-norm a p-norm>

Lineární regresní model, který pro regularizaci implementuje normu L1, se nazývá lasso regrese, a model, který pro regularizaci implementuje (kvadratickou) normu L2, se nazývá ridge regrese. Chcete-li implementovat tyto dva modely, všimněte si, že lineární regresní model zůstává stejný:

ale jde o výpočet ztrátové funkce, která zahrnuje tyto regularizační členy:

.

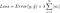
Pozn: Přesně řečeno, poslední rovnice (hřebenová regrese) je ztrátová funkce se čtvercovou normou L2 vah (všimněte si absence odmocniny). (Děkujeme Maxi Pechyonkinovi za upozornění na tuto skutečnost!)

Regularizační členy jsou „omezení“, kterých se musí optimalizační algoritmus „držet“ při minimalizaci ztrátové funkce, kromě toho, že musí minimalizovat chybu mezi skutečným y a předpovídaným ŷ.

1) Model

Definujme model, abychom viděli, jak fungují L1 a L2. Pro jednoduchost definujeme jednoduchý lineární regresní model ŷ s jednou nezávislou proměnnou.

Zde jsem použil konvence hlubokého učení w (‚weight‘) a b (‚bias‘).

V praxi nejsou jednoduché lineární regresní modely náchylné k nadměrnému přizpůsobení. Jak bylo zmíněno v úvodu, modely hlubokého učení jsou vzhledem ke složitosti modelu k takovým problémům náchylnější.

Proto si uvědomte, že výrazy použité v tomto článku lze snadno rozšířit i na složitější modely, které se neomezují pouze na lineární regresi.

2) Ztrátové funkce

Abychom demonstrovali vliv regularizace L1 a L2, fitujme náš lineární regresní model pomocí 3 různých ztrátových funkcí/cílů:

• L
• L1
• L2

Naším cílem je minimalizovat tyto různé ztráty.

2) Ztrátové funkce

L1

L2

Naším cílem je minimalizovat tyto různé ztráty.1) Ztrátová funkce bez regularizace

Ztrátovou funkci L definujeme jako kvadratickou chybu, kde chyba je rozdíl mezi y (skutečnou hodnotou) a ŷ (předpovídanou hodnotou).

Předpokládejme, že náš model bude pomocí této ztrátové funkce nadhodnocen.

2.2) Ztrátová funkce s regularizací L1

Vycházíme-li z výše uvedené ztrátové funkce a přidáme-li k ní člen regularizace L1, vypadá takto:

kde parametr regularizace λ > 0 je ručně doladěn. Nazvěme tuto ztrátovou funkci L1. Všimněte si, že |w| je diferencovatelná všude kromě případů, kdy w=0, jak je uvedeno níže. To budeme potřebovat později.

2. V tomto případě je nutné, abychom si uvědomili, že v tomto případě se jedná o tzv.3) Ztrátová funkce s L2 regularizací

Podobně vypadá přidání L2 regularizačního členu k L takto:

kde opět platí, že λ > 0.

3) Gradient Descent

Nyní vyřešíme lineární regresní model pomocí optimalizace gradient descent na základě výše definovaných 3 ztrátových funkcí. Připomeňme, že aktualizace parametru w při gradientním sestupu probíhá následovně:

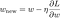
Poslední člen ve výše uvedené rovnici nahraďme gradientem L, L1 a L2 w.r.t. w.

L:

L1:

L2:

4) Jak se předchází nadměrnému přizpůsobení?

Odtud provedeme na výše uvedených rovnicích následující substituce (pro lepší čitelnost):

• η = 1,
• H = 2x(wx+b-y)

které nám dají

L:

L1:

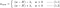
L2:

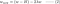
4.1) S regularizací vs. bez ní

Podívejte se na rozdíly mezi aktualizacemi vah s parametrem regularizace λ a bez něj. Zde je několik intuicí.

Intuice A:

Řekněme, že s rovnicí 0 nám výpočet w-H dává hodnotu w, která vede k nadměrnému přizpůsobení. Pak intuitivně rovnice {1.1, 1.2 a 2} sníží pravděpodobnost overfittingu, protože zavedení λ nás odkloní právě od w, které nám v předchozí větě mělo způsobit problémy s overfittingem.

Intuice B:

Řekněme, že overfitting modelu znamená, že máme hodnotu w, která je pro náš model ideální. ‚Perfektní‘ znamená, že kdybychom data (x) nahradili zpět v modelu, naše předpověď ŷ bude velmi, velmi blízko skutečnému y. Jistě, je to dobré, ale nechceme perfektní. Proč? Protože to znamená, že náš model je určen pouze pro množinu dat, na které jsme trénovali. To znamená, že náš model bude pro ostatní datové sady vytvářet předpovědi, které budou daleko od skutečné hodnoty. Spokojíme se tedy s méně než dokonalými s nadějí, že náš model dokáže získat blízké předpovědi i u jiných dat. Abychom toho dosáhli, „poskvrníme“ toto dokonalé w v rovnici 0 penalizačním členem λ. Tím získáme rovnice {1.1, 1.2 a 2}.

Intuice C:

Všimněte si, že H (jak je zde definováno) závisí na modelu (w a b) a datech (x a y). Aktualizace vah pouze na základě modelu a dat v rovnici 0 může vést k nadměrnému přizpůsobení, což vede ke špatné generalizaci. Naproti tomu v rovnicích {1.1, 1.2 a 2} je konečná hodnota w ovlivněna nejen modelem a daty, ale také předem definovaným parametrem λ, který je na modelu a datech nezávislý. Můžeme tedy zabránit nadměrnému přizpůsobení, pokud nastavíme vhodnou hodnotu λ, ačkoli příliš velká hodnota způsobí, že model bude silně podhodnocený.

Intuice D:

Edden Gerber (díky!) poskytl intuici o směru, kterým se naše řešení posouvá. Podívejte se do komentářů: https://medium.com/@edden.gerber/thanks-for-the-article-1003ad7478b2

4.2) L1 vs. L2

Nyní zaměříme pozornost na L1 a L2 a přepíšeme rovnice {1.1, 1.2 a 2} přeskupením jejich členů λ a H takto:

L1:

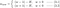
L2:

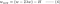
Srovnejte druhý člen každé z výše uvedených rovnic. Kromě H závisí změna w na členu ±λ nebo členu -2λw, které zvýrazňují vliv následujících faktorů:

1. značka aktuálního w (L1, L2)
2. velikost aktuálního w (L2)
3. zdvojnásobení parametru regularizace (L2)

Když na aktualizaci vah pomocí L1 má vliv první bod, na aktualizaci vah z L2 mají vliv všechny tři body. I když jsem toto srovnání provedl pouze na základě iterační aktualizace rovnice, uvědomte si, že to neznamená, že jedna z nich je „lepší“ než druhá.

Prozatím se níže podívejme, jak lze dosáhnout regularizačního efektu z L1 pouze znaménkem aktuálního w.

4.3) Vliv L1 na posouvání směrem k 0 (řídkost)

Podívejte se na L1 v rovnici 3.1.

. Pokud je w kladné, bude regularizační parametr λ>0 tlačit w do méně kladného stavu, a to odečtením λ od w. Naopak v rovnici 3.2, pokud je w záporné, bude λ přičteno k w a bude ho tlačit do méně záporného stavu. To má tedy za následek posunutí w směrem k 0.

To je samozřejmě zbytečné v lineárním regresním modelu s 1 proměnnou, ale osvědčí se to při „odstraňování“ zbytečných proměnných ve vícerozměrných regresních modelech. L1 si také můžete představit jako celkové snížení počtu funkcí v modelu. Zde je libovolný příklad, kdy se L1 snaží ‚vytlačit‘ některé proměnné ve vícerozměrném lineárním regresním modelu:

Jak tedy pomáhá vytlačení w směrem k 0 při overfittingu v regularizaci L1? Jak bylo zmíněno výše, s přechodem w k 0 snižujeme počet rysů tím, že snižujeme důležitost proměnné. Ve výše uvedené rovnici vidíme, že x_2, x_4 a x_5 jsou kvůli svým malým koeficientům téměř „zbytečné“, a proto je můžeme z rovnice odstranit. Tím se zase sníží složitost modelu, takže náš model bude jednodušší. Jednodušší model může snížit pravděpodobnost nadměrného přizpůsobení.

Poznámka

Přestože L1 má vliv na to, že tlačí váhy k 0, a L2 nikoli, neznamená to, že váhy se díky L2 nemohou dostat do blízkosti 0.

.