Varför är 0,999… lika med 1?!

Ett annat sätt att tänka på termerna i vår summering är att varje successiv term erhålls genom att multiplicera den föregående termen med ett gemensamt förhållande.

Det innebär att vi har en geometrisk serie som konvergerar mot a/(1 – r) där a är det första värdet i serien och r är förhållandet som vi multiplicerar med för att få nästa term.

Konvergens i en serie innebär helt enkelt att serien kommer att fortsätta att närma sig ett visst värde alltmer när man lägger till fler och fler termer i serien. Serien kommer oändligt nära konvergensvärdet. På en oändlig skala blir konvergens jämlikhet.

I vårt fall börjar vi med 1/10 och multiplicerar med 1/10 varje gång, så både a och r = 1/10.

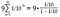
Färdigställ aritmetiken på höger sida.

Nu har vi formellt visat att 0.999… konvergerar till eller är lika med 1.

Sluttliga tankar & Inspiration

Om detta känns konstigt för dig är det bra! Du vet att två olika tal i själva verket borde vara olika tal. Den kontraintuitiva karaktären hos detta problem är inneboende i det märkliga som följer med att arbeta med oändligheten.

Även i ett enkelt problem som detta rör du dig från gränserna för vad som är gripbart för den mänskliga hjärnan till en skala som på sätt och vis ligger bortom vår fattningsförmåga. Som ändliga varelser kan vi gripa tag i att förstå begreppet oändlighet eller evighet, men vi kan aldrig riktigt uppleva det. Vilket innebär att det som vi vet är sant i vår ändliga värld ofta visar sig bete sig annorlunda på en oändlig nivå.

Acceptera övergången från lätt upptäckbar och reproducerbar matematik till det som bara kan testas och föreställas i våra sinnen är en del av matematikens skönhet och underverk.

Tag därför inte dagens lektion för vad den är värd och ryck på axlarna.

Låt det finnas ett lager av dimma mellan dig och den perfekta förståelsen. Låt ditt sinne bli blåst av det faktum att oändligheten beter sig märkligt. Och låt det få dig att längta efter mer förståelse och framför allt mer matematik.

Tack för att du läste och funderade över oändligheten tillsammans med mig i dag!