Vad händer om dina data INTE är normala?

Introduktion

Det är Halloween-vecka och mellan bus och godis skrattar vi datanördar åt den här gulliga memen i sociala medier.

Trodde du att detta var ett skämt? Låt mig säga er att detta inte är något att skratta åt. Det är skrämmande, helt i Halloween-anda!

Om vi inte kan anta att de flesta av våra data (av affärsmässigt, socialt, ekonomiskt eller vetenskapligt ursprung) åtminstone tillnärmelsevis är ”normala” (dvs. att de genereras av en Gauss-process eller av en summa av flera sådana processer), är vi dömda!

Här är en extremt kortfattad lista över saker som inte kommer att vara giltiga,

• Hela begreppet six-sigma
• Den berömda 68-95-99,7-regeln
• Det ”heliga” begreppet p=0,05 (kommer från 2 sigma-intervallet) i statistisk analys

Skrämmande nog? Låt oss prata mer om det…

Den allsmäktiga och allestädes närvarande normalfördelningen

Det här avsnittet ska vara kort och koncist.

Normalfördelningen (Gaussfördelningen) är den mest kända sannolikhetsfördelningen. Här är några länkar till artiklar som beskriver dess styrka och breda användbarhet,

• Varför datavetare älskar Gaussian

• Hur du dominerar statistikdelen av din intervju om datavetenskap
• Vad är det som är så viktigt med normalfördelningen?

På grund av att den förekommer inom olika områden och på grund av den centrala gränssatsen (CLT) intar den här fördelningen en central plats inom datavetenskap och analys.

Så, vad är problemet?

Det här är ju helt okej, vad är problemet?

Problemet är att du ofta kan hitta en fördelning för din specifika datamängd, som kanske inte uppfyller normaliteten, dvs. egenskaperna hos en normalfördelning. Men på grund av det överdrivna beroendet av antagandet om normalitet är de flesta ramverk för affärsanalys skräddarsydda för att arbeta med normalt fördelade datamängder.

Det är nästan inbäddat i vårt undermedvetna.

Säg att du ombeds att kontrollera om en ny datamängd från en viss process (teknik eller affärsverksamhet) är meningsfull. Med ”meningsfullt” menar du att de nya uppgifterna hör hemma, dvs. att de ligger inom det ”förväntade intervallet”.

Vad är denna ”förväntan”? Hur kvantifierar man intervallet?

Automatiskt, som om det styrs av en undermedveten drivkraft, mäter vi medelvärdet och standardavvikelsen för provdatasetetet och kontrollerar sedan om de nya uppgifterna ligger inom vissa standardavvikelser.

Om vi måste arbeta med en 95-procentig konfidensgräns är vi nöjda med att se att uppgifterna ligger inom 2 standardavvikelser. Om vi behöver en strängare gräns kontrollerar vi 3 eller 4 standardavvikelser. Vi beräknar Cpk, eller så följer vi six-sigma riktlinjer för ppm (parts-per-million) kvalitetsnivå.

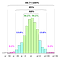
Alla dessa beräkningar bygger på det underförstådda antagandet att populationsdata (INTE stickprovet) följer Gaussisk distribution i.D.v.s. att den grundläggande processen, från vilken alla data har genererats (i det förflutna och för närvarande), styrs av mönstret på vänster sida.

Men vad händer om data följer mönstret på höger sida?

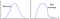
Och det här, och… det där?

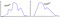
finns det en mer universell gräns när uppgifterna INTE är normala?

I slutändan kommer vi fortfarande att behöva en matematiskt sund teknik för att kvantifiera vår konfidensgräns, även om uppgifterna inte är normala. Det innebär att vår beräkning kan förändras lite, men vi bör fortfarande kunna säga något i stil med detta-

”Sannolikheten för att observera en ny datapunkt på ett visst avstånd från genomsnittet är sådan och sådan…”

Oppenbarligen måste vi söka efter en mer universell gräns än den omhuldade gaussiska gränsen på 68-95-99.7 (motsvarande 1/2/3 standardavvikelseavstånd från medelvärdet).

Turligtvis finns det en sådan gräns som kallas ”Chebyshev Bound”.

Vad är Chebyshev Bound och hur är den användbar?

Chebyshevs ojämlikhet (även kallad Bienaymé-Chebyshev ojämlikhet) garanterar att, för en bred klass av sannolikhetsfördelningar, inte mer än en viss bråkdel av värdena kan vara mer än ett visst avstånd från medelvärdet.

Specifikt kan inte mer än 1/k² av fördelningens värden vara mer än k standardavvikelser från medelvärdet (eller motsvarande, minst 1-1/k² av fördelningens värden ligger inom k standardavvikelser från medelvärdet).

Det gäller för praktiskt taget obegränsade typer av sannolikhetsfördelningar och fungerar utifrån ett mycket mer avslappnat antagande än normalitet.

Hur fungerar det?

Även om du inte vet något om den hemliga processen bakom dina data finns det en god chans att du kan säga följande,

”Jag är säker på att 75 % av alla data bör falla inom 2 standardavvikelser från medelvärdet”,

Och,

Jag är säker på att 89 % av alla data bör falla inom 3 standardavvikelser från medelvärdet”.

Här är hur det ser ut för en godtycklig fördelning,

Hur tillämpar man det?

Som du kan gissa vid det här laget behöver den grundläggande mekaniken för din dataanalys inte förändras ett dugg. Du kommer fortfarande att samla in ett urval av data (större ju bättre), beräkna samma två storheter som du är van vid att beräkna – medelvärde och standardavvikelse, och sedan tillämpa de nya gränserna i stället för 68-95-99,7-regeln.

Tabellen ser ut på följande sätt (här anger k så många standardavvikelser från medelvärdet),

En videodemo av dess tillämpning finns här,

Vad är haken? Varför använder inte folk denna ”mer universella” gräns?

Det är uppenbart vad haken är om man tittar på tabellen eller den matematiska definitionen. Chebyshev-regeln är mycket svagare än Gauss-regeln när det gäller att sätta gränser för data.

Den följer ett 1/k²-mönster jämfört med ett exponentiellt fallande mönster för normalfördelningen.

För att till exempel sätta gränser för något med 95 procents konfidens måste man inkludera data upp till 4,5 standardavvikelser mot. Det finns en annan avgränsning som kallas ”Chernoff Bound”/Hoeffding-ojämlikhet som ger en exponentiellt skarp svansfördelning (jämfört med 1/k²) för summor av oberoende slumpvariabler.

Detta kan också användas i stället för den gaussiska fördelningen när uppgifterna inte ser normala ut, men endast när vi har en hög grad av säkerhet om att den underliggande processen består av delprocesser som är helt oberoende av varandra.

Tyvärr är de slutliga uppgifterna i många sociala och affärsmässiga fall resultatet av ett extremt komplicerat samspel mellan många delprocesser som kan ha ett starkt inbördes beroende.

Sammanfattning

I den här artikeln har vi lärt oss om en särskild typ av statistisk avgränsning som kan tillämpas på bredast möjliga fördelning av uppgifter oberoende av antagandet om normalitet. Detta är praktiskt när vi vet mycket lite om den verkliga källan till data och inte kan anta att den följer en gaussisk fördelning. Gränsen följer en potenslag i stället för en exponentiell natur (som Gauss) och är därför svagare. Men det är ett viktigt verktyg att ha i sin repertoar för att analysera alla godtyckliga typer av datafördelningar.