Articles

Sum Of Product (SOP) & Product Of Sum (POS)

On november 10, 2021 by admin

Product Of Sum (POS) & Sum Of Product (SOP)

Tabellens innehållsförteckning

Sum Of Product (SOP)

Sum Of Product är en förkortad form av SOP. Sum of product form är en uttrycksform i boolesk algebra där olika produkttermer av indata summeras. Denna produkt är inte aritmetisk multiplikation utan den är boolesk logisk AND och summan är boolesk logisk OR.

För att bättre förstå SOP måste vi känna till min term.

Min Term

Minterm innebär den term som är sann för ett minsta antal kombinationer av indata. Det är sant för endast en kombination av ingångar.

Då AND-porten också ger True endast när alla dess ingångar är sanna så kan vi säga att mintermer är AND av ingångskombinationer som i tabellen nedan.

3 ingångar har 8 olika kombinationer. Varje kombination har en min-term som betecknas med ett litet m och dess decimala kombinationsnummer är skrivet i subscript. Var och en av dessa mintermer kommer endast att vara sann för den specifika inmatningskombinationen.

Du kanske också läser: Det finns några olika former av Sum of Product (SOP)-former
Det finns några olika former av Sum of Product (SOP)-former.
- Kanonisk SOP-form
- Non-kanonisk SOP-form
- Minimal SOP-form
Kanonisk SOP-form

Detta är standardformen för Sum of Product. Den bildas av O Ring mintermerna i den funktion för vilken utgången är sann. Detta är också känt som Sum of Min terms eller Canonical disjunctive normal form (CDNF). Det är bara ett fint namn. ”Kanonisk” betyder ”standardiserad” och ”disjunktiv” betyder ”logisk ELLER förening”.

Kanoniskt SOP-uttryck representeras av summeringstecknet ∑ och mintermer inom parentes för vilka utgången är sann.

Till exempel ges en funktions sanningstabell nedan.

För denna funktion är det kanoniska SOP-uttrycket

F = ∑( m1, m2, m3, m5 )

Vilket innebär att funktionen är sann för min-termerna {1, 2, 3, 5}.

Om vi expanderar summeringen får vi.

F = m1 + m2 + m3 + m5

Nu sätter vi in min-termer i uttrycket

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

Den kanoniska formen innehåller alla ingångar som antingen är kompletterade eller icke-kompletterade i sina produkttermer.

Du kan också läsa: Det är en icke-kanonisk SOP-form

Som namnet antyder är den här formen en icke standardiserad form av SOP-uttryck. Produkttermerna är inte min-termerna men de är förenklade. Låt oss ta ovanstående funktion i kanonisk form som ett exempel.

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

F = A̅B̅C + A̅B(C̅ + C) + AB̅C

F = A̅B̅C + A̅B(C̅ + C) + AB̅C

F = A̅B̅C + A̅BC + A̅C. A̅B(1) + AB̅C

F = A̅B̅C + A̅B + AB̅C

Detta uttryck är fortfarande i form av summa av produktform men det är intekanonisk eller icke-standardiserad form.

Minimal SOP-form

Denna form är det mest förenklade SOP-uttrycket för en funktion. Det är också en form av icke-kanonisk form. Minimal SOP-form kan göras med hjälp av booleska algebraiska satser, men den är mycket lätt att göra med hjälp av Karnaugh-mapp (K-map).

Minimal SOP-form är att föredra eftersom den använder ett minimalt antal grindar och inmatningslinjer. den är kommersiellt fördelaktig på grund av sin kompakta storlek, snabba hastighet och låga tillverkningskostnad.

Låt oss ta ett exempel på den funktion som ges ovan i kanonisk form.

Dess K-map ges nedan.

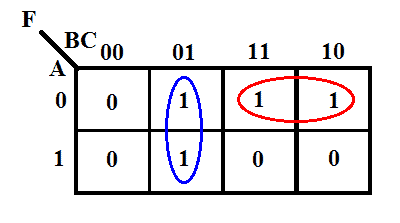
Enligt K-mappen blir utgångsuttrycket

F = B̅C + A̅B

Detta är det mest förenklade & optimerade uttrycket för nämnda funktion. Detta uttryck kräver endast två AND-portar med två ingångar & en OR-port med två ingångar. Den kanoniska formen kräver dock fyra AND-gates med tre ingångar & en OR-gate med fyra ingångar, vilket är relativt sett dyrare än implementeringen av den minimala formen.
- Du kanske också läser: Du kan också läsa mer om Ring Counter & Johnson Counter – Konstruktion & Drift
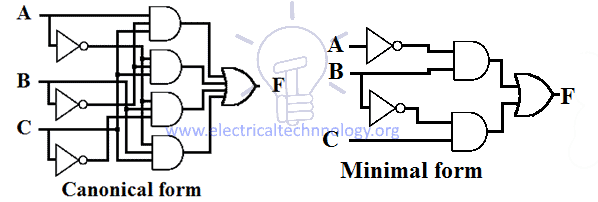
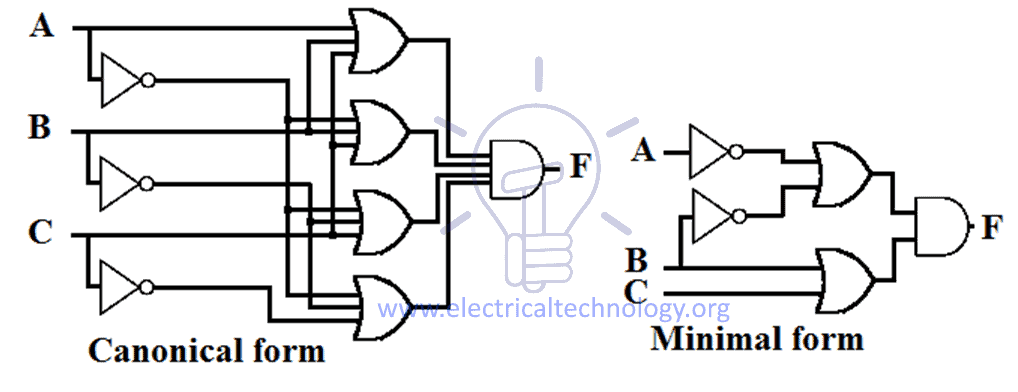
Schematisk utformning av Sum Of Product (SOP)

SOP-uttrycket implementerar en AND-OR-design på två nivåer där den första nivåns grind är en AND-grind som följs av den andra nivåns grind som är en OR-grind. Schematisk utformning av SOP-uttrycket kräver en grupp av AND-portar & en OR-port.

Varje SOP-uttryck har ungefär samma utformning, dvs. alla ingångar passerar genom AND-portar och sedan passerar utgången från dessa AND-portar genom en OR-port enligt figuren nedan.

Antalet av ingångar och antalet AND-portar beror på vilket uttryck man genomför.

Exempel på utformning av kanoniska och minimala SOP-uttryck för en funktion ges nedan.

Konvertering från minimal SOP-form till kanonisk SOP-form

Konvertering från minimal eller någon form av icke-kanonisk form till kanonisk form är mycket enkel.

Som vi vet har den kanoniska formen min-termer &min-termer består av alla ingångar, antingen kompletterade eller icke-komplementerade. Vi multiplicerar alltså varje term i den minimala SOP:n med summan av de saknade ingångsvärdenas kompletterade och icke-kompletterade form. Exempel på konvertering för ovanstående funktion i minimal SOP-form ges nedan:

Minimal SOP-form

F = A̅B + B̅C

Term A̅B saknar ingång C. Vi multiplicerar alltså A̅B med (C+C̅) eftersom (C+C̅ = 1). Termen B̅C saknar input A. Så den multipliceras med (A+A̅)

F = A̅B(C + C̅) + B̅C(A + A̅)

F = A̅BC + A̅BC̅ + AB̅C + A̅B̅C

Nu är detta uttryck i kanonisk form.

Konvertering från kanonisk SOP till kanonisk POS

Standard SOP-uttryck kan konverteras till standard POS-uttryck (produkt av summa). Exempelvis är funktionen ovan i kanonisk SOP-form

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

F = ∑ ( m1, m2, m3, m5 )

De återstående termerna i denna funktion är maxtermer för vilka utgången är falsk. Dessa maxtermer är M0,M4,M6,M7. Dessa maxtermer kommer att användas i POS-uttrycket som produkten av dessa maxtermer. Symbolen för produkten är ∏.

F = ∏ ( M0, M4, M6, M7)

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C)(A̅+B̅+C̅)

Max-termerna är komplementet till min-termer. Därför är M0=(A+B+C).
- Du kanske också läser: Omvandling från kanoniskt SOP till minimalt SOP
  Kanoniskt SOP kan omvandlas till minimalt SOP. Den kan konverteras med hjälp av Karnaugh-mappning eller booleska algebraiska satser. K-map-metoden är mycket enkel och dess exempel har gjorts ovan i minimal SOP-form.
  
  Summaprodukt
  
  Summaprodukt förkortat POS.
  
  Summaproduktformen är en form där produkter av olika summatermer av indata tas. Dessa är inte aritmetiska produkt och summa utan de är logiska booleska AND respektive OR.
  
  För att bättre förstå Summaprodukt måste vi känna till Maxterm.
  
  Maxterm
  
  Maxterm innebär den term eller det uttryck som är sant för ett maximalt antal ingångskombinationer eller som är falskt för endast en kombination av ingångarna.
  
  Då OR-porten också ger falskt för endast en ingångskombination. Maxterm är alltså OR för antingen kompletterade eller icke-kompletterade ingångar.
  
  Maxtermer för 3 ingångsvariabler ges nedan.
  
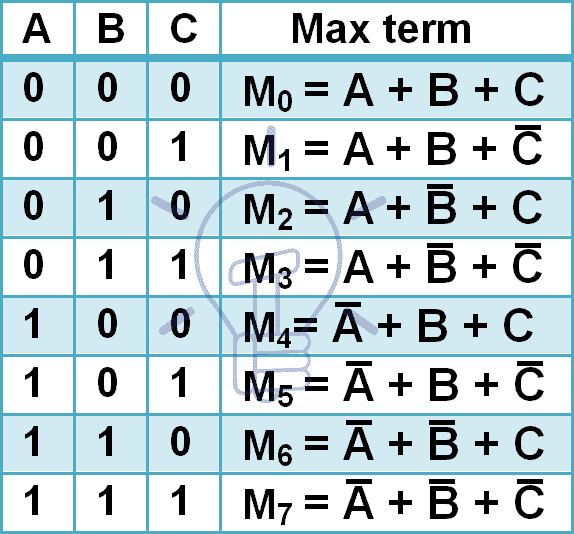
  3 ingångar har 8 olika kombinationer så det kommer att ha 8 maxtermer. Maxtermer betecknas med stort M och decimalkombinationsnummer i subscript som visas i tabellen ovan.
  
  I maxterm är varje ingång kompletterad eftersom Maxterm ger ”0” endast när den nämnda kombinationen tillämpas och Maxterm är komplement till minterm.
  
  M3 = m̅3
  
  M3 = (A̅BC)’
  
  M3 = A + B̅ +C̅ DE Morgans lag
  
  Det är därför som för A=0 Maxterm består av A & för A=1 Maxterm består av A̅.
  
  Du kan också läsa: Du kan också läsa följande: Digitala flip-flops – SR-, D-, JK- och T-flipflops
  
  Typer av produkt av summaformer
  
  Det finns olika typer av produkt av summaformer.
  - Canonical POS Form
  - Non – Canonical Form
  - Minimal POS Form
  Canonical POS Form
  
  Det är också känt som Product of Max term eller Canonical conjunctive normal form (CCNF). Kanonisk betyder standard och konjunktiv betyder korsning.
  
  I den här formen är Maxterms AND tillsammans för vilket resultatet är falskt.
  
  Kanoniskt POS-uttryck representeras av ∏ och Maxterms för vilket resultatet är falskt inom parentes enligt exemplet nedan.
  
  F = ∏ (M0, M4, M6, M7)
  
  Expanderar produkten
  
  F = M0.M4.M6.M7
  
  Sätta in Max-termer
  
  F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)
  
  Den kanoniska formen innehåller alla ingångar som antingen är kompleterade eller icke-kompleterade i dess varje Sum-term.
  - Du kan också läsa: Det är en av de viktigaste frågorna som du kan läsa om: Clap Switch Circuit Electronic Project Using 555 Timer
  Icke-kanonisk form
  
  Produkten av ett summauttryck som inte är i standardform kallas icke-kanonisk form.
  
  Låt oss ta den ovan angivna funktionen som exempel.
  
  F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)
  
  F = (B+C) (A̅+B̅+C)(A̅+B̅+C)(A̅+B̅+C̅)
  
  Samma men omvända termer eliminerar från två Max-termer och bildar en enda term för att bevisa det här är ett exempel.
  
  = (A+B+C) (A̅+B+C)
  
  = AA̅+AB+AC+A̅B+BB+BC+A̅C+BC+CC
  
  = 0+AB+AC+A̅B+A̅C+B+B+C+C
  
  = A(B+C)+A̅(B+C)+B(1+C)+C
  
  = (B+C)(A+A̅)+B(1)+C
  
  = (B+C)(0)+B+C
  
  = B+C
  
  Det uppnådda uttrycket är fortfarande i form av produkt av summa men det är intekanonisk form.
  
  Minimal POS-form
  
  Detta är den mest förenklade och optimerade formen av ett POS-uttryck som inte är kanoniskt. Minimal produkt av summaformen kan uppnås med hjälp av booleska algebraiska satser som i det icke-kanoniska exemplet ovan. En annan metod för att uppnå minimal POS-form är att använda Karnaugh-mappning, vilket är jämförelsevis enklare än att använda Boolska algebraiska satser.
  
  Minimal POS-form använder mindre antal ingångar och logiska grindar under genomförandet, varför de föredras framför den kanoniska formen på grund av deras kompakta, snabba och billiga genomförande.
  
  Låt oss ta den ovan givna funktionen som exempel
  
  K-map av funktionen
  
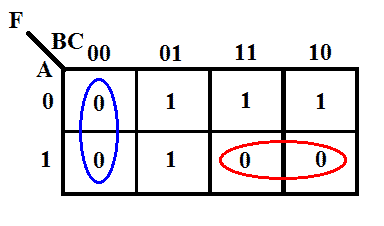
  Minimalt uttryck med hjälp av K-map
  
  F = (B+C) (A̅+B̅)
  
  Det uppnådda uttrycket är den minimala produkten av summaformen. Det är fortfarande Produkt av summa-uttryck Men det behöver bara 2 ingångar två OR-portar och en enda AND-port med 2 ingångar. Den kanoniska formen behöver dock 4 OR-portar med 3 ingångar och 1 AND-port med 4 ingångar.
  - Du kanske också läser: Du kan också läsa: Negativ återkoppling och förstärkarsystem med negativ återkoppling
  Schematisk utformning av summaprodukt (POS)
  
  Uttrycket summaprodukt har en specifik schematisk utformning av OR-AND. I OR-AND går ingångarna genom en rad OR-portar som är den första nivån av portar, utgången från den första nivån av OR-portar går genom den andra nivån av portar,som är en AND-port.
  
  Antalet ingångar och antalet portar som används i denna konstruktion beror på uttrycket som ska implementeras.
  
  Den kanoniska formen består av det maximala antalet möjliga ingångar och portar, men den minimala formen består av det lägsta möjliga antalet ingångar och portar. Den schematiska utformningen av den kanoniska och minimala POS-formen ges nedan.
  
  Konvertering från minimal POS till kanonisk form POS
  
  Som vi vet har den kanoniska formen av POS max termer och max termer innehåller varje ingång, antingen kompletterad eller icke-kompletterad. Vi kommer därför att lägga till varje summarisk term med produkten av kompletterad och icke-kompletterad saknad input. Exempel på dess omvandling ges nedan.
  
  Minimal POS-form
  
  F = (A̅+B̅) (B+C)
  
  (A̅+B̅) termen saknar C-inmatning så vi kommer att lägga till (CC̅) med den. (B+C) termen saknar A input så vi kommer att lägga till (AA̅) med den.
  
  F = (A̅+B̅+CC̅) (B+C+AA̅)
  
  F = (A̅+B̅+C)(A̅+B̅+C̅)(A+B+C)(A̅+B+C)(A̅+B+C)
  
  Detta uttryck har nu sin kanoniska form.
  - Du kan också läsa: Omvandling från kanonisk form av POS till SOP
    Summans produktuttryck kan omvandlas till summa av produktform endast om uttrycket är i kanonisk form. Kanonisk POS och kanonisk SOP är interkonvertibla dvs. de kan konverteras till varandra. Ett exempel på omvandling av POS till SOP ges nedan.
    
    POS kanonisk form
    
    F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)
    
    I den kanoniska formen är varje summauttryck ett maxuttryck så det kan också skrivas som:
    
    F = ∏(M0,M4,M6,M7)
    
    De återstående kombinationerna av ingångar är mintermer av funktionen för vilka dess utgång är sann. För att omvandla det till ett SOP-uttryck ändrar vi först symbolen till summering (∑) och använder den återstående mintermen.
    
    F = ∑ (m1,m2,m3,m5)
    
    Nu expanderar vi summeringstecknet för att bilda ett kanoniskt SOP-uttryck.
    
    F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C
    
    Min-termer är komplement till Max-termer för samma kombination av ingångar.
    
    Kanonisk till Minimal POS
    
    Ett kanoniskt uttryck för summaprodukt kan omvandlas till en form för minimal summaprodukt med hjälp av en Karnaugh-karta (K-map). En annan metod för att omvandla kanonisk till minimal är att använda booleska algebraiska satser.
    
    Användningen av K-map är mycket enkel varför K-map är att föredra. För minimala POS-uttryck kombineras 0:orna i K-map till grupper och det uttryck vi får är kompletterat eftersom grupperna består av ”0:or”. Dess exempel har gjorts ovan.
    
    Du kanske också läser:
    - Digital Logic NOT Gate – Digital Inverter Logic Gate
    - Exclusive-NOR (XNOR) Digital Logic Gate
    - Digital Logic NOR Gate
    - Digital Logic NAND Gate