Funktioner eller kartläggning

Nu ska vi i funktioner eller kartläggning studera en speciell typ av relationer som kallas funktioner eller kartläggning. För att förstå dem tar vi några exempel från verkligheten.

Alla dessa frågor har
unika svar. Låt oss
se hur vi kan relatera
det här i inlärningskartläggning.

● Varifrån går solen upp?

Öster

● Vilken är Indiens huvudstad?

Delhi

● Vad är efterföljaren till 4?

5

● Vad är summan av 5 och 3?

8

Mappning eller funktioner:

Om A och B är två icke-tomma mängder, sägs en relation ”f” från mängden A till mängden B vara en funktion eller mappning,
● Om varje element i mängden A är förknippat med ett unikt element i mängden B.

● Funktionen ”f” från A till B betecknas med f : A → B.

● Om f är en funktion från A till B och x ∈ A, så är f(x) ∈ B där f(x) kallas bilden av x under f och x kallas förbilden av f(x) under ’f’.

Note:

För att f ska vara en avbildning från A till B:

● Varje element i A måste ha en bild i B. Den intilliggande figuren representerar inte en avbildning eftersom elementet d i mängden A inte är associerat med något element i mängden B.

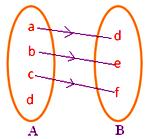
● Inget element i A får ha mer än en bild. Den intilliggande figuren representerar inte en avbildning eftersom element b i mängden A är associerat med två element d, f i mängden B.

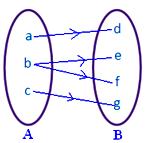
● Olika element i A kan ha samma bild i B. Bredvidliggande figur representerar en avbildning.

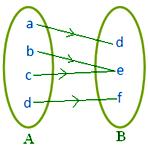
Anmärkning:

Varje avbildning är en relation, men varje relation kanske inte är en avbildning.

Funktion som en speciell typ av relation:

Låt oss påminna om och granska funktionen som en speciell typ av relation om man antar att A och B är två icke-tomma mängder så kallas en regel ”f” som associerar varje element i A med ett unikt element i B för en funktion eller en kartläggning från A till B.
Om ’f’ är en avbildning från A till B,

uttrycker vi det som f: A → B

läser vi det som att ’f’ är en funktion från A till B.
Om ’f ’ är en funktion från A till B och x∈A och y∈B, säger vi att y är elementets x:s avbild under funktionen ’ f ’ och betecknar det med f(x).
Därmed skriver vi det som y = f(x)

Här kallas element x för förebild till y.

För en funktion från A till B gäller alltså att
● A och B ska vara icke-tomma.

● Varje element i A ska ha en bild i B.

● Inget element i ”A” ska ha mer än en bild i ”B”.
Anmärkningar:

● Två eller flera element i A kan ha samma bild i B.

● f : x → y innebär att under funktionen ”f” från A till B har ett element x i A bild y i B.

● Det är nödvändigt att varje f-bild finns i B, men det kan finnas vissa element i B som inte är f-bilder till något element i A.

● Relationer och avbildningar

Ordnat par

Kartesisk produkt av två mängder

Relation

Domän och räckvidd för en relation

Funktioner eller avbildningar

Domän Co-funktionens domän och räckvidd

● Relationer och kartläggning – Arbetsblad

Arbetsblad om matematiska relationer

Arbetsblad om funktioner eller kartläggning

Matematiska problem i sjunde klass

Matematiska övningar i åttonde klass
Från funktioner eller kartläggning till HEMSIDAN