Datastrukturer: Staplar och köer – Designveloper

Varför staplar och köer?

Till skillnad från en matris finns det i staplar och köer ingen slumpmässig åtkomst (vi kan inte komma åt ett element direkt med ett index). Vi har vanligtvis färre metoder/åtgärder som vi kan utföra, t.ex. push(), pop(), peek(), enqueue(), dequeue(), som alla uteslutande behandlar elementet i början eller slutet av datastrukturen.

Men…

Fråga: Detta låter så begränsande eftersom vi bara kan få tillgång till det första eller sista elementet i datastrukturen. Varför skulle vi någonsin vilja använda något sådant här? Varför använder vi inte bara matriser för mer flexibilitet?

Svar: Staplar och köer är vanligtvis ”datastrukturer på högre nivå” som byggs ovanpå datastrukturer på lägre nivå (matriser eller länkade listor) för att begränsa de operationer vi kan utföra på dem. Det är en fördel om vi vill ha begränsad åtkomst.

Att ha denna begränsade förmåga på en datastruktur är en fördel eftersom vi kan kontrollera vem som använder denna datastruktur som endast utför rätt operationer som är effektiva. Vi behöver till exempel inte undra om någon slumpmässigt har infogat ett element i mitten av vår lista, vilket ställer till det för några invarianter. Det räddade oss från många problem. Låt oss titta närmare på dem.

Vad är en stapel?

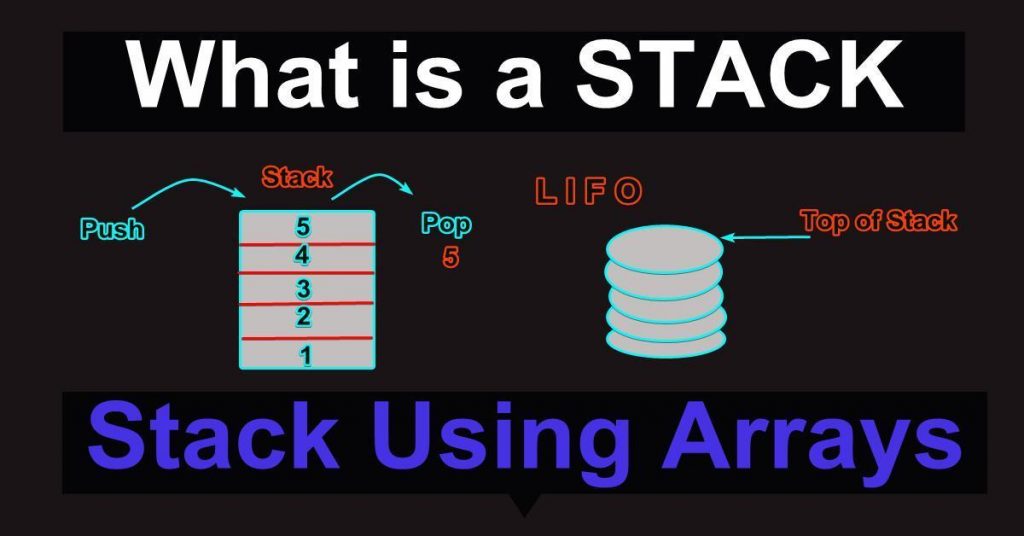
En stapel är en linjär datastruktur med ett slut som modellerar en riktig stapel genom att ha två primära operationer, nämligen push och pop.

I den här bilden nedan ser vi att en datamedlem tas bort från stackens topp och en annan läggs till den. Det finns en topppekare som pekar på blocket högst upp på stapeln. Detta beror på att element i en stapel alltid tas bort och läggs till högst upp i högen. Detta beteende är allmänt känt som LIFO (Last In First Out).

Stackoperationer

Nedan följer de 2 grundläggande operationerna som kan utföras på en stapel.

• Pushfunktion: Lägg till ett element på toppen av stapeln
• Pop-funktion: Ta bort det översta elementet (och eventuellt returnera det)

Visualisering av stackens grundläggande operationer

Det finns dessutom följande ytterligare funktioner för en stapel för att kontrollera dess status.

• Peek-funktion: Funktion: Returnerar det översta elementet i stapeln utan att ta bort eller radera det
• isEmpty-funktion: Kontrollera om stapeln är tom eller inte
• isFull-funktion: Kontrollera om stapeln är full eller inte

Allt fungerar på toppen av stapeln. Vi har inte tillgång till något annat än toppen. Detta är avgörande för att förstå hur det fungerar.

Komplexitetsanalys

Den följande komplexitetstabellen utgår från att du har implementerat en stack med hjälp av en länkad lista

Stacktillämpningar

Hur och var används en stack? Vi använder Stack mycket i programmering utan att ens märka det, här är några exempel:

• Kan användas för uttrycksutvärdering (t.ex. en algoritm för att analysera och utvärdera matematiska uttryck).
• Kan användas för att implementera funktionsanrop i rekursionsprogrammering.

• Används av ångra mekanismer i textredigerare för att ångra text som vi har skrivit (Cmd + Z på Mac OS och Ctrl + Z på Windows)
• Används i webbläsare för att navigera bakåt och. framåt
• Kan användas för att göra en DFS (Depth First Search) i en graf
• Används bakom kulisserna för att stödja rekursion genom att hålla reda på tidigare funktionsanrop

Vad är en kö?

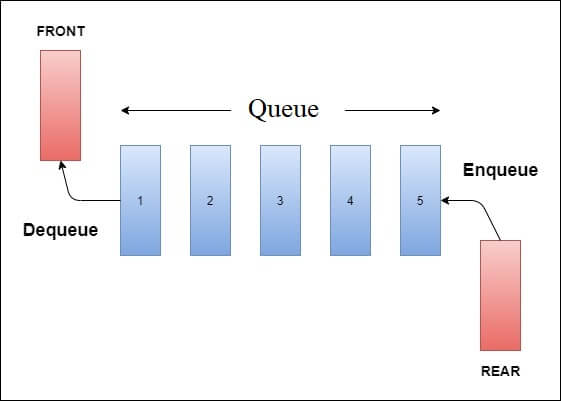
En kö är också en linjär datastruktur som modellerar verkliga köer genom att ha två primära operationer, nämligen enqueue (vi kan tänka oss det som ”gå in i kön”) och dequeue (vi kan också tänka oss det som ”ta bort från kön”). Denna struktur kallas ”kö” på grund av att den liknar en verklig kö – (där människor väntar i en kö).

Alla köer har en främre och en bakre ände (ibland kallad ”bakre”). Vi lägger in element genom baksidan och tar bort dem genom framsidan.

En kö är en FIFO-struktur (First In First Out – det element som placeras först kan nås först) som är vanlig i många programmeringsspråk.

Köoperationer

Följande är de tre grundläggande operationer som kan utföras på en kö.

• Enqueue-funktion: Lägg till ett element i slutet av kön
• Dequeue-funktion: Lägg till ett element i slutet av kön
• Dequeue-funktion: Lägg till ett element i slutet av kön: Ta bort ett element från början av kön
• Peeking-funktion: Titta på värdet längst fram i kön utan att ta bort det

Komplexitetsanalys

Som vi kan se i bilden tar enqueuing- och dequeuing-operationer konstant tid O(1). Att kontrollera om ett element finns i kön är dock linjär tid O(n) eftersom vi potentiellt skulle behöva skanna igenom alla element.

Det finns också en intern borttagning av element (inte avköning). Det kräver linjär tid eftersom vi måste skanna igenom alla element i värsta fall.

Kötillämpningar

• Används för att hantera trådar i multithreading.
• Kan användas för att effektivt hålla reda på de x senast tillagda elementen
• Hantering av förfrågningar från webbservern där vi vill ha först till kvarn. Till exempel: Vi vill ha ett exempel: Vid varje given tidpunkt kan vår webbserver endast betjäna upp till högst 50 personer samtidigt.

Om 70 förfrågningar kommer in under en kort tidsperiod kommer vi inte att kunna behandla alla. Därför tar webbservern endast 50 förfrågningar från kön och lägger de återstående 20 i vänteläge. När webbservern är klar med att behandla en begäran tar den bort nästa begäran och fortsätter att göra det tills kön är tom.

• Breadth-first search (BFS) graph traversal
• Används för att implementera kösystem (t.ex.: prioritetsköer)
• Används i nätverksskrivare: Skrivaren kan endast betjäna en enda begäran åt gången. Så om andra förfrågningar kommer när skrivaren är upptagen kommer programmet som hanterar skrivaren inte att avvisa dessa förfrågningar utan lägga dem i en kö i väntan på att de ska utföras. Den första begäran kommer att betjänas först (FIFO).

Vi hoppas att den här artikeln har gett dig en bild av staplar och köer i åtanke. Glöm inte att prenumerera på vår blogg och följ Designvelopers Facebook, Twitter och LinkedIn.

Och det här är andra artiklar som du kanske gillar:

• Vad är arkitektur för webbapplikationer?
• Datastrukturer och deras tillämpningar
• Vad är Big O-notation?