2.12: Van der Waals ekvation

En ekvation från van der Waals utökar ekvationen för ideala gaser på ett enkelt sätt. Van der Waals ekvation är

\

Den passar tryck-volym-temperaturdata för en verklig gas bättre än vad idealgasekvationen gör. Den förbättrade anpassningen erhålls genom att införa två parametrar (betecknade ”\(a\)” och ”\(b\)”) som måste bestämmas experimentellt för varje gas. Van der Waals ekvation är särskilt användbar i vår strävan att förstå beteendet hos verkliga gaser, eftersom den förkroppsligar en enkel fysisk bild av skillnaden mellan en verklig gas och en idealgas.

När vi härleder Boyles lag från Newtons lagar antar vi att gasmolekylerna inte interagerar med varandra. Enkla argument visar att detta bara kan vara ungefärligt sant. Verkliga gasmolekyler måste interagera med varandra. På korta avstånd stöter de bort varandra. På något längre avstånd drar de till sig varandra. Ekvationen för den ideala gasen kan också härledas från de grundläggande antaganden som vi gör i § 10 genom en tillämpning av teorin om statistisk termodynamik. Genom att göra olika antaganden om molekylära egenskaper kan vi tillämpa statistisk termodynamik för att härleda\({}^{5}\) van der Waals ekvation. De nödvändiga antagandena är att molekylerna upptar en ändlig volym och att de attraherar varandra med en kraft som varierar som en omvänd potens av avståndet mellan dem. (Den attraherande kraften antas vanligen vara proportionell mot \(r^{-6}\).)

För att inse att verkliga gasmolekyler både attraherar och stöter bort varandra behöver vi bara komma ihåg att vilken gas som helst kan göras flytande genom att sänka dess temperatur och öka det tryck som tillämpas på den. Om vi kyler vätskan ytterligare fryser den till ett fast ämne. Två utmärkande egenskaper hos ett fast ämne är att det behåller sin form och att det är nästan inkompressibelt. Vi tillskriver ett fast materials inkompressibilitet till repulsiva krafter mellan dess ingående molekyler; de har kommit så nära varandra att repulsiva krafter mellan dem har blivit viktiga. För att komprimera det fasta ämnet måste molekylerna tryckas ännu närmare varandra, vilket kräver orimliga krafter. Om vi å andra sidan kastar en iskupa tvärs över rummet flyger alla dess vattenmolekyler tillsammans tvärs över rummet. Uppenbarligen attraheras vattenmolekylerna i fast substans av varandra, annars skulle de alla gå sin egen väg – att kasta iskuber skulle vara som att kasta en handfull torr sand. Men vattenmolekyler är samma molekyler oavsett temperatur eller tryck, så om det finns attraktions- och repulsionskrafter mellan dem i fast form måste dessa krafter också finnas i vätske- och gasfasen.

I gasfasen är molekylerna långt ifrån varandra; i vätske- eller fast form är de packade tillsammans. Vid kokpunkten är volymen av en vätska mycket mindre än volymen av den gas från vilken den kondenseras. Vid fryspunkten skiljer sig volymen av ett fast ämne bara lite från volymen av den vätska från vilken det fryser, och den är definitivt större än noll. Dessa vardagliga observationer förklaras lätt genom att anta att varje molekyl har en karakteristisk volym. Vi kan förstå att detta i sin tur är en följd av de intermolekylära krafternas karaktär; uppenbarligen blir dessa krafter starkare när avståndet mellan ett par molekyler minskar. Eftersom en vätska eller ett fast ämne upptar en bestämd volym måste den avstötande kraften öka snabbare än den attraherande kraften när det intermolekylära avståndet är litet. Ofta är det lämpligt att tala om den molära volymen för en kondenserad fas. Med molär volym menar vi volymen av en mol av ett rent ämne. Den molära volymen i en kondenserad fas bestäms av det intermolekylära avståndet vid vilket det råder balans mellan intermolekylära attraktions- och repulsionskrafter.

Evidens är molekylerna mycket nära varandra i kondenserade faser. Om vi antar att tomrummen mellan molekylerna är försumbara är volymen av en kondenserad fas ungefär lika med antalet molekyler i provet multiplicerat med volymen av en enda molekyl. Den molära volymen är då Avogadros tal gånger den volym som upptas av en molekyl. Om vi känner till densiteten, D, och den molära massan, \(\overline{M}\), kan vi hitta den molära volymen, \(\overline{V}\), som

\

Den volym som upptas av en molekyl, V\({}_{molekyl}\), blir

\

Trycket och volymen i van der Waals ekvation är den verkliga gasens tryck och volym. Vi kan relatera termerna i van der Waals ekvation till den ideala gasekvationen: Det är användbart att tänka på termerna \(\left(P+{{{{an}^2}/{V^2}\right)\) och \(\left(V-nb\right)\) som trycket och volymen för en hypotetisk idealgas. Det vill säga

\ &=nRT \end{align*}\]

Då har vi

\

\

Vi härleder den ideala gasekvationen från en modell där molekylerna är icke interagerande punktmassor. Volymen av en idealgas är alltså den volym som upptas av en gas vars enskilda molekyler har noll volym. Om de enskilda molekylerna i en verklig gas effektivt upptar en volym \({b}/{\overline{N}}}\), så upptar \(n\) mol av dem effektivt en volym

\

Van der Waals ekvation säger att volymen av en verklig gas är den volym som skulle upptas av icke samverkande punktmassor, \(V_{ideal\ gas}\), plus den effektiva volymen av gasmolekylerna själva. (När data för verkliga gasmolekyler anpassas till van der Waals ekvation är värdet av \(b\) vanligen något större än den volym som uppskattas från vätskans densitet och molekylvikt. Se problem 24.)

Så har vi

\

Vi kan förstå detta som en logisk följd av attraktiva interaktioner mellan molekylerna i den verkliga gasen. Med \(a>0\) säger det att trycket i den verkliga gasen är lägre än trycket i den hypotetiska ideala gasen, med en mängd som är proportionell mot \({\left({n}/{V}\right)}^2\). Proportionalitetskonstanten är \(a\). Eftersom \({n}/{V}\) är gasmolekylernas molära densitet (mol per volymenhet) är det ett mått på koncentrationen. Antalet kollisioner mellan molekyler av samma slag är proportionellt mot kvadraten på deras koncentration. (Vi behandlar denna punkt mer ingående i kapitel 4 och 5.) Så \({\left({n}/{V}\right)}^2\) är ett mått på frekvensen med vilken de verkliga gasmolekylerna kommer i nära kontakt med varandra. Om de attraherar varandra när de kommer nära varandra bör effekten av denna attraktion vara proportionell mot \({\left({n}/{V}\right)}^2\). Så van der Waals ekvation stämmer överens med idén att trycket i en verklig gas skiljer sig från trycket i den hypotetiska ideala gasen med en mängd som är proportionell mot frekvensen och styrkan i de attraktiva växelverkningarna.

Men varför skulle de attraktiva växelverkningarna ha denna effekt; varför skulle trycket i den verkliga gasen vara lägre än trycket i den hypotetiska ideala gasen? Det kanske bästa sättet att utveckla en kvalitativ bild är att inse att attraktiva intermolekylära krafter tenderar att få gasmolekylerna att klumpa ihop sig. Det är trots allt dessa attraktiva krafterattraktiva krafter som gör att molekylerna samlas till en vätska vid låga temperaturer. Ovanför kokpunkten begränsar gasmolekylernas förmåga att gå skilda vägar effekterna av denna tendens, men även i gasen måste de attraktiva krafterna verka på ett sätt som tenderar att minska den volym som upptas av molekylerna. Eftersom den volym som gasen upptar dikteras av behållarens storlek – inte av gasens egenskaper i sig själv – kommer denna tendens till klumpning till uttryck som en minskning av trycket.

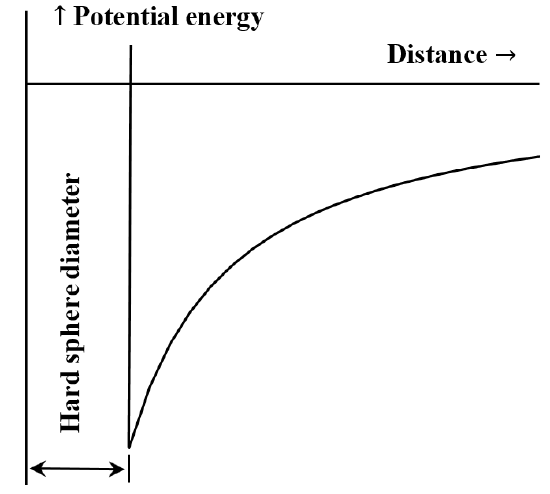
Det är ofta användbart att beskriva interaktionen mellan partiklar eller kemiska enheter i form av ett diagram över potentiell energi i förhållande till avstånd. Van der Waals ekvation motsvarar fallet att den repulsiva interaktionen mellan molekyler är obefintlig tills molekylerna kommer i kontakt med varandra. När de väl kommer i kontakt blir den energi som krävs för att flytta dem ännu närmare varandra godtyckligt stor. Ofta beskrivs detta genom att säga att de beter sig som ”hårda sfärer”. Attraktionskraften mellan två molekyler minskar när avståndet mellan dem ökar. När de är mycket långt ifrån varandra är den attraktiva växelverkan mycket liten. Vi säger att interaktionsenergin är noll när molekylerna är oändligt långt ifrån varandra. Om vi till en början har två långt ifrån varandra belägna, stationära, ömsesidigt attraherande molekyler, kommer de spontant att röra sig mot varandra och få kinetisk energi när de går. Deras potentiella energi minskar när de närmar sig varandra och når sitt minsta värde när molekylerna kommer i kontakt med varandra. Van der Waals ekvation innebär således det diagram över potentiell energi kontra avstånd som skisseras i figur 5.