Articles

Soma do Produto (SOP) & Produto da Soma (POS)

On Novembro 10, 2021 by admin

Produto da Soma (POS) & Soma do Produto (SOP)

Soma do Produto (SOP)

Soma do Produto é a forma abreviada do SOP. A soma da forma do produto é uma forma de expressão em álgebra booleana na qual diferentes termos de entrada do produto estão sendo somados. Este produto não é aritmético multiplicar mas é lógico Booleano AND e a Soma é lógica Booleana OR.

Para entender melhor sobre SOP, precisamos saber sobre o termo min.

Termo Mínimo

Minterm significa o termo que é verdadeiro para um número mínimo de combinações de inputs. Isso é verdade apenas para uma combinação de inputs.

Since AND gate também dá True apenas quando todos os seus inputs são verdadeiros, então podemos dizer que os termos min são AND de combinações de inputs como na tabela abaixo.

3 inputs têm 8 combinações diferentes. Cada combinação tem um min de termos denotado por pequeno m e seu número decimal de combinação escrito em subscrito. Cada um destes minterms só será verdadeiro para a combinação de entrada específica.

• Você também pode ler: Contador Assíncrono Digital (Contador de Ondas) – Tipos, Trabalho & Aplicação

Tipos de Soma do Produto (SOP) Formulários

Existem poucas formas diferentes de Soma do Produto.

• Formulário SOP Canónico
• Formulário SOP Não Canónico
• Formulário SOP Dinâmico

>

Formulário SOP Canónico

Esta é a forma padrão da Soma do Produto. É formado por O Ring os minterms da função para a qual a saída é verdadeira. Esta também é conhecida como Soma dos termos Min ou forma normal disjuntiva canônica (CDNF). É apenas um nome extravagante. “canônico” significa “padronizado” e “disjuntivo” significa “união lógica OU”.

Expressão canônica SOP é representada pelo sinal de soma ∑ e os minterms nas chaves para as quais a saída é verdadeira.

Por exemplo, uma tabela de verdade de funções é dada abaixo.

>Para esta função a expressão canônica SOP é

F = ∑( m1, m2, m3, m5 )

O que significa que a função é verdadeira para os termos min {1, 2, 3, 5}.

Aumentando a soma que obtemos.

F = m1 + m2 + m3 + m5

Agora colocando os termos min na expressão

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

A forma canónica contém todos os inputs complementados ou não complementados nos termos do seu produto.

Você também pode ler: Contador Síncrono Digital – Tipos, Trabalho & Aplicações

Formulário SOP Não-Canônico

Como o nome sugere, este formulário é a forma não-padronizada de expressões SOP. Os termos do produto não são os termos min, mas eles são simplificados. Vamos tomar a função acima em forma canônica como exemplo.

F = A̅BC̅C + A̅B̅ + AB̅C + C̅

F = C̅̅C + A̅B(A̅B + C) + ̅C

F = ̅C̅C + A̅B(1) + AB̅C

F = A̅B̅C + A̅B + AB̅C

Esta expressão ainda está na forma de Soma do Produto mas nãoforma canônica ou não padronizada.

Formulário SOP mínimo

Este formulário é a expressão SOP mais simplificada de uma função. É também uma forma de forma não canônica. O formulário SOP mínimo pode ser feito usando teoremas algébricos booleanos, mas é muito fácil de fazer usando o mapa de Karnaugh (K-map).

O formulário SOP mínimo é preferido porque usa o número mínimo de portões e linhas de entrada. é comercialmente benéfico devido ao seu tamanho compacto, velocidade rápida, e baixo custo de fabricação.

Vejamos um exemplo da função dada acima em forma canônica.

Its K-map é dado abaixo.

>

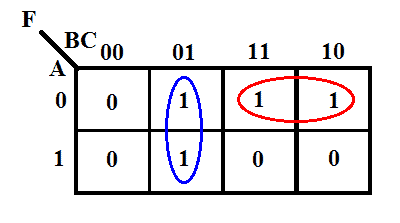
De acordo com o K-map, a expressão de saída será

F = B̅C + A̅B

Esta é a expressão mais simplificada & expressão optimizada para a referida função. Esta expressão requer apenas duas portas de 2 entradas E portas & uma porta de 2 entradas OU. Entretanto, a forma canônica precisa de quatro portas de 3 entradas E portões & uma porta de 4 entradas OU, que é relativamente mais cara que a implementação mínima da forma.

• Você também pode ler: Contador de anéis & Contador Johnson – Construção & Operação

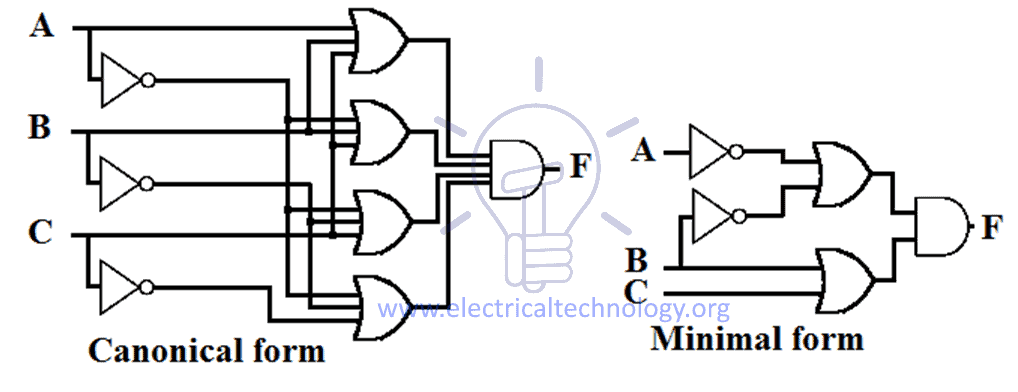
Desenho esquemático da soma do produto (SOP)

ExpressãoSOP implementa 2 níveis AND-OR desenho no qual o portão de 1º nível é AND depois do portão de 2º nível que é OR portão. O desenho esquemático da expressão SOP precisa de um grupo de portas AND &uma porta OR.

A expressão SOP tem um desenho um pouco igual, ou seja, todas as entradas passam por AND gate e então a saída destas AND gates passam por uma porta OR como mostrado na figura abaixo.

O número de entradas e o número de portas AND dependem da expressão que está sendo implementada.

Exemplo de desenhos de expressão canônica e mínima SOP para uma função é dado abaixo.

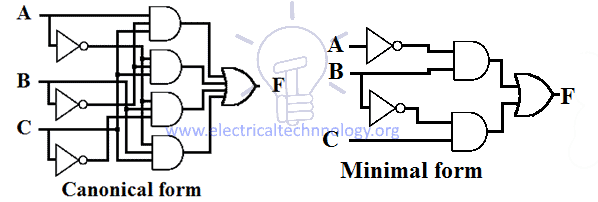
Conversão de SOP Mínimo para SOP Canonical Form

Conversão de forma mínima ou qualquer tipo de forma não canônica para forma canônica é muito simples.

Como sabemos a forma canônica tem termos min & termos min consiste em todos os inputs complementados ou não complementados. Então multiplicaremos cada termo do SOP mínimo com a soma dos inputs que faltam na forma complementada e não-completada. Exemplo de conversão para a função acima na forma do SOP mínimo é dado abaixo.

F = A̅B + B̅C

O termo A̅B está faltando o input C. Então multiplicaremos A̅B com (C+C̅) porque (C+C̅ = 1). O termo B̅C está faltando a entrada A. então ele será multiplicado com (A+A̅)

F = A̅B(C + C̅) + B̅C(A + A̅)

F = A̅BC + A̅BC̅ + AB̅C + A̅B̅C

Agora, esta expressão está em forma canônica.

Conversão do SOP canônico para POS canônico

Expressão padrão do SOP pode ser convertida em expressão padrão POS (produto da soma). Por exemplo, a função dada acima está na forma canónica SOP

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

F = ∑ ( m1, m2, m3, m5 )

Os restantes termos desta função são maxterms para os quais a saída é falsa. Estes termos máximos são M0,M4,M6,M7. Estes termos máximos serão usados na expressão POS como o produto destes termos máximos. O Símbolo do Produto é ∏.

F = ∏ ( M0, M4, M6, M7)

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

Os termos Máximo são o complemento dos termos minterms. É por isso que M0=(A+B+C).

• Você também pode ler: Ripple Carry And Carry Look Ahead Adder

Conversão do SOP Canónico para SOP Mínimo

SOP Canónico pode ser convertido para SOP mínimo. Ele pode ser convertido usando mapa de Karnaugh ou teoremas algébricos booleanos. O método K-map é muito fácil e seu exemplo foi feito acima no formulário SOP mínimo.

Produto da Soma

Produto da Soma abreviado para POS.

O produto do formulário da Soma é uma forma na qual produtos de diferentes termos de soma de entradas são tomados. Estes não são produto aritmético e soma, mas são lógicos Booleanos AND e OR respectivamente.

Para entender melhor sobre o Produto da Soma, precisamos saber sobre o termo Max.

Termos Max.

Maxterm significa o termo ou expressão que é verdadeiro para um número máximo de combinações de inputs ou que é falso para apenas uma combinação de inputs.

Since OR gate também dá falso para apenas uma combinação de inputs. Então Maxterm é OU de entradas complementadas ou não-comentadas.

Termos máximos para 3 variáveis de entrada são dados abaixo.

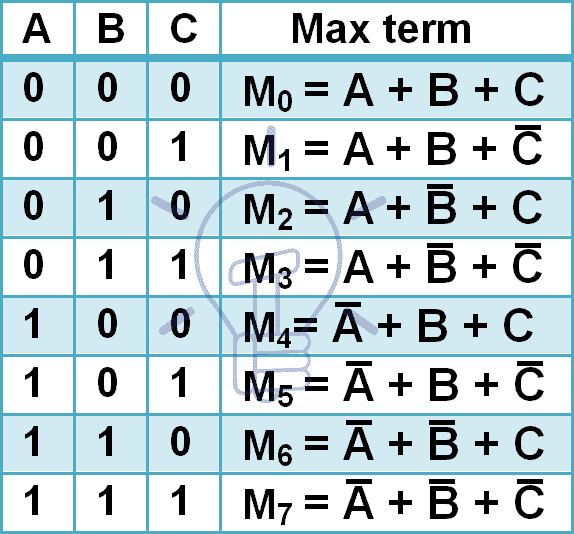
3 entradas têm 8 combinações diferentes, portanto terá 8 maxtermos. Maxterms são denotados por M maiúsculo e número de combinação decimal No subscrito como mostra a tabela acima.

Em maxterm, cada input é complementado porque Maxterm dá ‘0’ somente quando a combinação mencionada é aplicada e Maxterm é complemento de minterm.

M3 = m̅3

M3 = (A̅BC)’

M3 = A + B̅ +C̅ DE Morgan’s law

Por isso para A=0 o termo máximo consiste em A & para A=1 o termo máximo consiste em A̅.

Você também pode ler: Digital Flip-Flops – SR, D, JK e T Flip Flops

Tipos de Formulários de Produto de Soma

Existem diferentes tipos de Formulários de Produto de Soma.

• Formulário POS Canónico
• Não – Formulário Canónico
• Formulário POS Dinâmico

>

Formulário POS Canónico

É também conhecido como Produto do termo Max ou forma normal conjuntiva canónica (CCNF). Canonical significa padrão e conjuntivo significa intersecção.

Neste formulário, Maxterms são AND juntos para os quais a saída é falsa.

Expressão canónica POS é representada por ∏ e Maxterms para os quais a saída é falsa entre parênteses como mostrado no exemplo dado abaixo.

F = ∏ (M0, M4, M6, M7)

Expandindo o produto

F = M0.M4.M6.M7

>Pondo termos máximos

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

A forma canónica contém todas as entradas complementadas ou não complementadas em cada termo da Soma.

• Vocês também podem ler: Clap Switch Circuit Electronic Project Using 555 Timer

Non – Canonical Form

O produto da expressão de soma que não está na forma padrão é chamado de forma não canônica.

Vamos tomar a função acima dada como exemplo.

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

F = (B+C) (A̅+B̅+C)(A̅+B̅+B̅)

Os mesmos termos, mas invertidos, eliminam de dois termos Max e formam um único termo para prová-lo aqui é um exemplo.

= (A+B+C) (A̅+B+C)

= A̅C+AB+AC+A̅B+BB+BC+A̅B+BC+CC

= 0+AB+AC+A̅B+A̅B+B+BC+C

= A(B+C)+A̅(B+C)+B(1+C)+C

= (B+C)(A+A̅)+B(1)+C

= (B+C)(0)+B+C

= B+C

> A expressão alcançada ainda está na forma de Produto da Soma, mas nãoforma canónica.

Formulário POS mínimo

Esta é a forma mais simplificada e optimizada de uma expressão POS que não é canónica. O produto mínimo da forma Soma pode ser alcançado usando teoremas algébricos booleanos como no exemplo não-canônico dado acima. Outro método para alcançar a forma mínima de POS é usando o mapa de Karnaugh, que é comparativamente mais fácil do que usar os teoremas algébricos booleanos.

Forma POS minimalista usa menos entradas e portões lógicos durante sua implementação, por isso eles estão sendo preferidos em relação à forma canônica por sua implementação compacta, rápida e de baixo custo.

Vejamos como exemplo a função dada acima

K-map da função

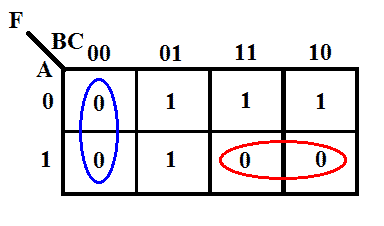
Expressão mínima usando K-map

F = (B+C) (A̅+B̅)

A expressão alcançada é o produto mínimo da forma de soma. Ela ainda é produto da expressão Soma, mas precisa apenas de 2 entradas duas portas OU uma única entrada E uma porta de 2 entradas. Entretanto, a forma canônica precisa de 4 portas OU de 3 entradas e 1 porta E de 4 entradas.

• Você também pode ler: Sistemas Amplificadores de Retorno Negativo e de Retorno Negativo

Desenho Esquemático do Produto da Soma (POS)

O produto da expressão Soma tem um desenho esquemático específico de OR-AND. Em OR-AND as entradas passam por uma matriz de portas OR que é o primeiro nível de portas, a saída do primeiro nível de portas OR passa pelo segundo nível da porta,que é uma porta AND.

O número de entradas e o número de portas utilizadas neste projeto depende da expressão que será implementada.

A forma canônica consiste no número máximo de entradas e portas possíveis, no entanto, a forma mínima consiste no menor número possível de entradas e portas. O desenho esquemático da forma canônica e mínima do POS é dado abaixo.

Conversão do POS mínimo para a forma canônica do POS

Como sabemos a forma canônica do POS tem termos máximos e os termos máximos contêm cada entrada complementada ou não complementada. Assim, vamos adicionar cada termo de soma com o produto de entrada complementado e não-completado em falta. Exemplo da sua conversão é dado abaixo.

Mínimo formulário POS

F = (A̅+B̅) (B+C)

(A̅+B̅) termo está faltando C input, então vamos adicionar (CC̅) com ele. (B+C) está faltando o termo A, então vamos adicionar (AA̅) com ele.

F = (A̅+B̅+CC̅) (B+C+AA̅)

F = (A̅+B̅+C)(A̅+B̅+C̅)(A+B+C)(A̅+B+C)

Esta expressão está agora em forma canônica.

• Você também pode ler: Contador e Tipos de Contadores Eletrônicos

Conversão de POS Canônico para SOP

O produto da expressão Soma só pode ser convertido na forma de Soma do Produto se a expressão estiver na forma canônica. Os POS canónicos e os SOP canónicos são inter-conversíveis, ou seja, podem ser convertidos uns nos outros. Um exemplo de conversão de POS para SOP é dado abaixo.

POS forma canônica

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

Em forma canônica cada termo de soma é um termo máximo para que também possa ser escrito como:

F = ∏(M0,M4,M6,M7)

As restantes combinações de entradas são minterms da função para a qual a sua saída é verdadeira. Para convertê-la em expressão SOP primeiro vamos mudar o símbolo para soma (∑) e usar o mintermo restante.

F = ∑ (m1,m2,m3,m5)

Agora vamos expandir o sinal de soma para formar a expressão SOP canônica.

> F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

Termos Mínimos são um complemento dos termos Máximo para a mesma combinação de entradas.

POS Canónico para Mínimo

Um Produto Canónico da expressão Soma pode ser convertido em Produto Mínimo da forma de soma usando o mapa de Karnaugh (K-map). Outro método para converter canônico em mínimo é usando teoremas algébricos booleanos.

O uso do K-map é muito fácil, é por isso que K-map é preferido. Para expressão POS mínima, os 0’s no K-map são combinados em grupos e a expressão que obtemos é complementada desde que os grupos foram feitos de ‘0’s. O seu exemplo foi feito acima.

Você também pode ler:

• Digital Logic NOT Gate – Digital Inverter Logic Gate
• Exclusive-NOR (XNOR) Digital Logic Gate
• Digital Logic NOR Gate
• Digital Logic NAND Gate