Suma Produsului (SOP) și Produsul Sumei (POS)

Produsul Sumei (POS) & Suma Produsului (SOP)

Suma Produsului (SOP)

Suma Produsului este forma prescurtată a SOP. Forma Sum of product este o formă de expresie în algebra booleană în care diferiți termeni produs ai intrărilor sunt însumați împreună. Acest produs nu este o înmulțire aritmetică, ci este un ȘI logic boolean, iar suma este un OR logic boolean.

Pentru a înțelege mai bine SOP, trebuie să cunoaștem termenul minim.

Termen minim

Minterm înseamnă termenul care este adevărat pentru un număr minim de combinații de intrări. Adică este adevărat pentru o singură combinație de intrări.

Din moment ce poarta AND dă, de asemenea, Adevărat numai atunci când toate intrările sale sunt adevărate, astfel încât putem spune că termenii min sunt AND de combinații de intrări ca în tabelul de mai jos.

3 intrări au 8 combinații diferite. Fiecare combinație are un termen min notat cu m mic și numărul său de combinație zecimală scris în subscript. Fiecare dintre acești termeni min va fi adevărat doar pentru combinația specifică de intrare.

• Ai putea citi și:
  • Ai putea citi, de asemenea: Digital Asynchronous Counter (Ripple Counter) – Tipuri, funcționare & Aplicație

  Tipuri de forme de Sum of Product (SOP)

  Există câteva forme diferite de Sum of Product.

  • Forma SOP canonică
  • Forma SOP necanonică
  • Forma SOP minimală

  Forma SOP canonică

  Este forma standard de Sum of Product. Ea este formată din O Inel de mintermeni ai funcției pentru care ieșirea este adevărată. Aceasta este cunoscută și sub numele de Sum of Min terms sau Canonical disjunctive normal form (CDNF). Este doar o denumire sofisticată. „Canonic” înseamnă „standardizat”, iar „disjunctiv” înseamnă „Unire logică OR”.

  Expresia SOP canonică este reprezentată prin semnul de sumă ∑ și mintermeni în paranteze pentru care ieșirea este adevărată.

  De exemplu, tabelul de adevăr al unei funcții este dat mai jos.

  

  Pentru această funcție, expresia SOP canonică este

  F = ∑( m1, m2, m3, m5 )

  Ceea ce înseamnă că funcția este adevărată pentru termenii min {1, 2, 3, 5}.

  Prin extinderea sumei obținem.

  F = m1 + m2 + m3 + m5

  Acum punând termenii min în expresie

  F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

  Forma canonică conține toate intrările fie completate, fie necompletate în termenii produsului său.

  Ai putea citi și:

  Formă canonică: Contor digital sincronizat – Tipuri, funcționare & Aplicații

  Forma SOP necanonică

  După cum sugerează și numele, această formă este forma nestandardizată a expresiilor SOP. Termenii produsului nu sunt termenii min, dar sunt simplificați. Să luăm ca exemplu funcția de mai sus în forma canonică.

  F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

  F = A̅B̅C + A̅B(C̅ + C) + AB̅C

  F = A̅B̅C + AB̅C

  F = A̅B̅C + A̅B(1) + AB̅C

  F = A̅B̅C + A̅B + AB̅C

  Această expresie este încă în forma de sumă de produse, dar este non-canonică sau formă nestandardizată.

  Forma SOP minimală

  Această formă este cea mai simplificată expresie SOP a unei funcții. Este, de asemenea, o formă de formă necanonică. Forma SOP minimală poate fi realizată cu ajutorul teoremelor algebrice booleene, dar este foarte ușor de realizat cu ajutorul hărții Karnaugh (K-map).

  Forma SOP minimală este preferată deoarece utilizează un număr minim de porți și linii de intrare. este benefică din punct de vedere comercial datorită dimensiunii sale compacte, vitezei rapide și costului redus de fabricație.

  Să luăm un exemplu al funcției date mai sus în formă canonică.

  

  Harta sa K-map este dată mai jos.

  

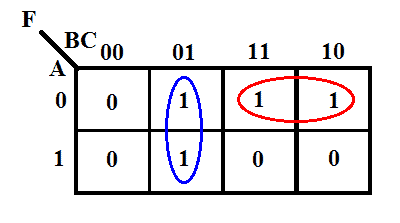
  Conform K-map-ului, expresia de ieșire va fi

  F = B̅C + A̅B

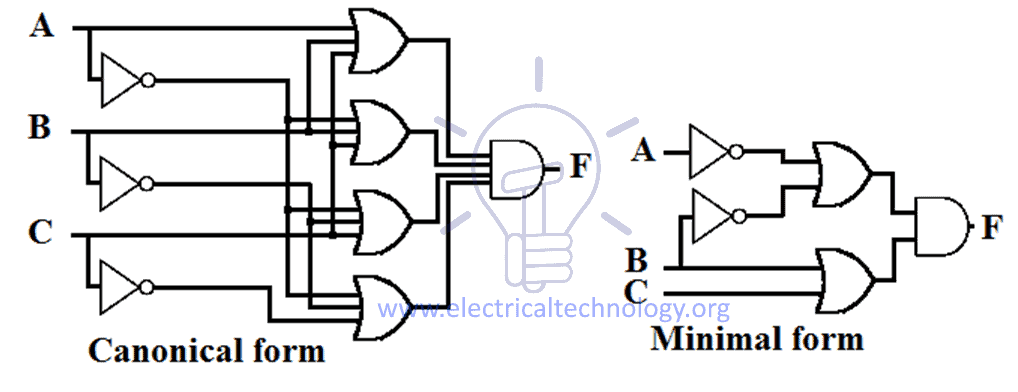
  Aceasta este cea mai simplificată & expresie optimizată pentru funcția menționată. Această expresie necesită doar două porți AND cu 2 intrări & o poartă OR cu 2 intrări. Cu toate acestea, forma canonică are nevoie de patru porți AND cu 3 intrări & o poartă OR cu 4 intrări, ceea ce este relativ mai costisitor decât implementarea formei minimale.

  • Ai putea citi și: &Ceea mai mare parte din această expresie este reprezentată de o poartă AND cu 3 intrări: Contor inelar & Contor Johnson – Construcție & Funcționare

  Proiectarea schematică a sumei produsului (SOP)

  Expresia SOP implementează un design AND-OR pe 2 nivele în care poarta de la nivelul 1 este o poartă AND care urmează poarta de la nivelul 2 care este o poartă OR. Proiectarea schematică a expresiei SOP necesită un grup de porți AND & o poartă OR.

  Fiecare expresie SOP are oarecum aceeași concepție, adică toate intrările trec printr-o poartă AND și apoi ieșirea acestor porți AND trece printr-o poartă OR, așa cum se arată în figura de mai jos.

  Numărul de intrări și numărul de porți AND depind de expresia pe care o implementează.

  Exemplu de proiectare a expresiei SOP canonice și minime pentru o funcție este dat mai jos.

  

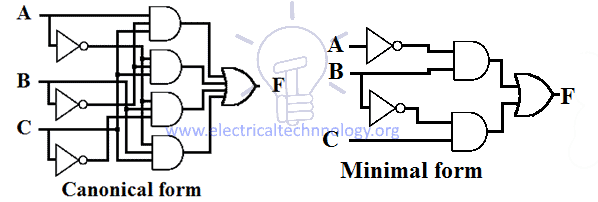
  Conversia de la forma SOP minimă la forma SOP canonică

  Conversia de la forma minimă sau orice fel de formă necanonică la forma canonică este foarte simplă.

  După cum știm, forma canonică are termeni minimi & Termenii minimi constau din toate intrările, fie completate, fie necompletate. Așadar, vom înmulți fiecare termen al SOP minimal cu suma formelor completate și necompletate ale intrărilor lipsă. Exemplul de conversie pentru funcția de mai sus în forma minimă SOP este dat mai jos.

  Forma minimă SOP

  F = A̅B + B̅C

  Termenul A̅B este intrarea lipsă C. Deci vom înmulți A̅B cu (C+C̅) deoarece (C+C̅ = 1). Termenului B̅C îi lipsește intrarea A. deci va fi înmulțit cu (A+A̅)

  F = A̅B(C + C̅) + B̅C(A + A̅)

  F = A̅BC + A̅BC̅ + AB̅C + A̅B̅C

  Acum, această expresie este în formă canonică.

  Conversia din SOP canonic în POS canonic

  Expresia SOP standard poate fi convertită în expresie POS (produs de sumă) standard. De exemplu, funcția dată mai sus este în forma SOP canonică

  F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

  F = ∑ ( m1, m2, m3, m5 )

  Termenii rămași din această funcție sunt maxtermeni pentru care ieșirea este falsă. Acești termeni maxtermeni sunt M0,M4,M6,M7. Acești termeni max vor fi utilizați în expresia POS ca produs al acestor termeni max. Simbolul produsului este ∏.

  F = ∏ ( M0, M4, M6, M7)

  F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅+C̅)(A̅+B̅+C̅)

  Termenii Max sunt complementul termenilor mintermeni. De aceea, M0=(A+B+C).

  • Ai putea citi și: M0=(A+B+C): Ripple Carry And Carry Look Ahead Adder

  Conversia din SOP canonic în SOP minim

  SOP canonic poate fi convertit în SOP minim. Acesta poate fi convertit folosind harta Karnaugh sau teoremele algebrice booleene. Metoda K-map este foarte ușoară și exemplul său a fost realizat mai sus în forma SOP minimală.

  Produs de sumă

  Produs de sumă prescurtat POS.

  Forma produs de sumă este o formă în care se iau produsele a diferiților termeni de sumă ai intrărilor. Acestea nu sunt produsul și suma aritmetică, ci sunt produse logice booleene AND și, respectiv, OR.

  Pentru a înțelege mai bine produsul sumei, trebuie să cunoaștem termenul Max.

  Termenul Max

  Termenul Max înseamnă termenul sau expresia care este adevărată pentru un număr maxim de combinații de intrări sau care este falsă pentru o singură combinație de intrări.

  Din moment ce poarta OR dă, de asemenea, fals pentru o singură combinație de intrări. Deci Maxterm este OR fie al intrărilor completate, fie al intrărilor necompletate.

  Termenii maximi pentru 3 variabile de intrare sunt dați mai jos.

  

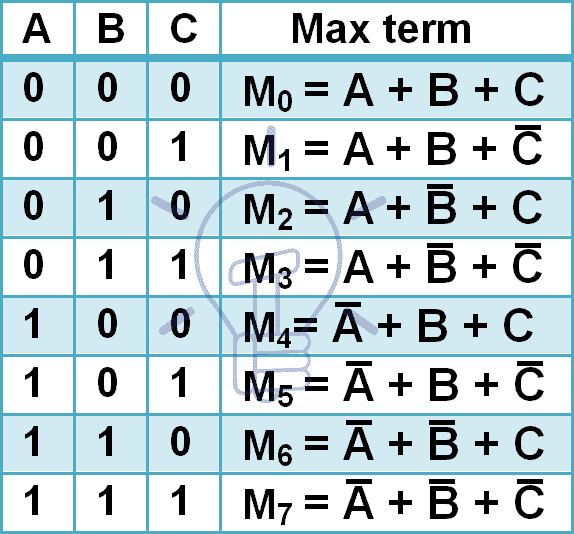
  3 intrări au 8 combinații diferite, deci vor avea 8 maxtermeni. Maxtermele sunt notate cu majusculă M și numărul combinației zecimale în subsol, așa cum se arată în tabelul de mai sus.

  În maxtermen, fiecare intrare este completată, deoarece Maxterm dă „0” numai atunci când se aplică combinația menționată și Maxterm este complementul mintermenului.

  M3 = m̅3

  M3 = (A̅BC)’

  M3 = A + B̅ +C̅ DE legea lui Morgan

  De aceea, pentru A=0 termenul maxim constă în A & pentru A=1 termenul maxim constă în A̅.

  Ai putea citi și:

  : Flip-Flops digitale – Flip-Flops SR, D, JK și T

  Tipuri de forme de produs al sumei

  Există diferite tipuri de forme de produs al sumei.

  • Forma POS canonică
  • Forma non-canonică
  • Forma POS minimală

  Forma POS canonică

  Este cunoscută și sub numele de Produs al termenului maxim sau Forma normală conjunctivă canonică (CCNF). Canonică înseamnă standard și conjunctivă înseamnă intersecție.

  În această formă, Maxtermele sunt AND împreună pentru care ieșirea este falsă.

  Expresia POS canonică este reprezentată prin ∏ și Maxtermele pentru care ieșirea este falsă în paranteze, așa cum se arată în exemplul de mai jos.

  

  F = ∏ (M0, M4, M6, M7)

  Extinderea produsului

  F = M0.M4.M6.M7

  Prinderea termenilor Max

  F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅+C̅)

  Forma canonică conține toate intrările fie completate, fie necompletate în fiecare termen al sumei sale.

  • Ai putea citi și: M7: Clap Switch Circuit Clap Switch Circuit Electronic Project Using 555 Timer

  Forma non – canonică

  Produsul expresiei sumă care nu este în formă standard se numește formă necanonică.

  Să luăm ca exemplu funcția dată mai sus.

  F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

  F = (B+C) (A̅+B̅+C)(A̅+B̅+C̅)(A̅+B̅+C̅)

  .

  La fel, dar termenii inversați elimină din doi termeni Max și formează un singur termen pentru a o demonstra iată un exemplu.

  = (A+B+C) (A̅+B+C)

  = AA̅+AB+AC+A̅B+BB+BC+A̅C+BC+CC

  = 0+AB+AC+A̅B+A̅C+B+B+B+C+C

  = A(B+C)+A̅(B+C)+B(1+C)+C

  .

  = (B+C)(A+A̅)+B(1)+C

  = (B+C)(0)+B+C

  = B+C

  Expresia obținută este tot sub formă de Produs de sumă, dar este nonforma canonică.

  Forma POS minimală

  Aceasta este forma cea mai simplificată și optimizată a unei expresii POS care este necanonică. Forma Minimal Product of Sum poate fi obținută folosind teoreme algebrice booleene, ca în exemplul necanonic dat mai sus. O altă metodă de obținere a formei POS minime este prin utilizarea hărții Karnaugh, care este comparativ mai ușoară decât utilizarea teoremelor algebrice booleene.

  Forma POS minimă utilizează un număr mai mic de intrări și porți logice în timpul implementării sale, motiv pentru care este preferată în locul formei canonice pentru implementarea compactă, rapidă și cu costuri reduse.

  Să luăm ca exemplu funcția dată mai sus

  K-map a funcției

  

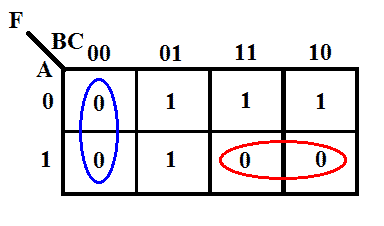
  Expresia minimă folosind K-map

  F = (B+C) (A̅+B̅)

  Expresia obținută este produsul minim al formei sumă. Este tot o expresie de produs al sumei Dar are nevoie doar de 2 intrări două porți OR și o singură poartă AND cu 2 intrări. Cu toate acestea, forma canonică are nevoie de 4 porți OR de 3 intrări și de 1 poartă AND de 4 intrări.

  • Ai putea citi și: Cealaltă formă canonică are nevoie de 4 porți OR de 3 intrări și de 1 poartă AND de 4 intrări: Sisteme amplificatoare cu reacție negativă și cu reacție negativă

  Proiectarea schematică a produsului sumei (POS)

  Expresia produs al sumei are o proiectare schematică specifică de tip OR-AND. În OR-AND, intrările trec printr-o matrice de porți OR, care reprezintă primul nivel de porți, iar ieșirea de la primul nivel de porți OR trece prin cel de-al doilea nivel de porți, care este o poartă AND.

  Numărul de intrări și numărul de porți utilizate în acest design depinde de expresia care urmează să fie implementată.

  Forma canonică constă în numărul maxim de intrări și porți posibile, însă forma minimă constă în cel mai mic număr posibil de intrări și porți. Proiectarea schematică a formei POS canonice și minime este prezentată mai jos.

  

  Conversia din POS minim în POS forma canonică

  După cum știm, forma canonică a POS are maximum de termeni, iar termenii maximi conțin fiecare intrare, fie completată, fie necompletată. Așadar, vom adăuga fiecare termen sumă cu produsul intrărilor lipsă completate și necompletate. Exemplul de conversie a acesteia este dat mai jos.

  Forma POS minimală

  F = (A̅+B̅) (B+C)

  (A̅+B̅) termenul este intrarea C lipsă, astfel că vom adăuga (CC̅) cu acesta. Termenului (B+C) îi lipsește intrarea A, așa că vom adăuga (AA̅) la acesta.

  F = (A̅+B̅+CC̅) (B+C+AA̅)

  F = (A̅+B̅+C)(A̅+B̅+C̅)(A̅+C̅)(A+B+C)(A̅+B+C)

  Această expresie este acum în formă canonică.

  • Puteți citi și: F = (A̅+B̅+C̅) Contoare și tipuri de contoare electronice

  Conversia din POS canonic în SOP

  Expresia produs al sumei poate fi convertită în forma sumă de produse numai dacă expresia este în formă canonică. POS canonic și SOP canonic sunt interconvertibile, adică pot fi convertite una în alta. Exemplul de conversie din POS în SOP este dat mai jos.

  Forma canonică POS

  F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅+C̅+C̅)

  În forma canonică, fiecare termen de sumă este un termen maxim, astfel încât se poate scrie și sub forma:

  F = ∏(M0,M4,M6,M7)

  Celelalte combinații de intrări sunt mintermeni ai funcției pentru care ieșirea sa este adevărată. Pentru a o converti în expresie SOP mai întâi vom schimba simbolul în însumare (∑) și vom folosi mintermii rămași.

  F = ∑ (m1,m2,m3,m5)

  Acum vom extinde semnul de însumare pentru a forma expresia SOP canonică.

  F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

  Termenii Min sunt complementul termenilor Max pentru aceeași combinație de intrări.

  POS canonic la minim

  Un produs canonic al expresiei de sumă poate fi convertit în produsul minim al formei de sumă prin utilizarea hărții Karnaugh (K-map). O altă metodă de convertire a expresiei canonice în minimală este prin utilizarea teoremelor algebrice booleene.

  Utilizarea K-map este foarte ușoară, de aceea K-map este preferată. Pentru o expresie POS minimală, „0”-urile din K-map sunt combinate în grupuri, iar expresia pe care o obținem este completată, deoarece grupurile au fost formate din „0”-uri. Exemplul său a fost realizat mai sus.

  Ai putea citi și:

  • Portă logică digitală NOT – Poartă logică digitală cu invertor
  • Portă logică digitală EXCLUSIV-NOR (XNOR)
  • Portă logică digitală NOR
  • Portă logică digitală NAND

  .