Funcții sau cartografiere

Acum, în cadrul funcțiilor sau cartografierii vom studia un tip special de relații numite funcții sau cartografiere. Pentru a le înțelege, să luăm câteva exemple din viața reală.

Toate aceste întrebări au
răspunsuri unice. Haideți să
vedem cum putem relaționa
acestea în cartografierea învățării.

● De unde răsare soarele?

Est

● Care este capitala Indiei?

Delhi

● Care este succesorul lui 4?

5

● Care este suma dintre 5 și 3?

8

Mapping sau funcții:

Dacă A și B sunt două seturi nevide, atunci o relație „f” din setul A în setul B se spune că este o funcție sau mapping,
● Dacă fiecărui element al setului A i se asociază un element unic al setului B.

● Funcția „f” din A în B se notează cu f : A → B.

● Dacă f este o funcție de la A la B și x ∈ A, atunci f(x) ∈ B unde f(x) se numește imaginea lui x sub f și x se numește preimaginea lui f(x) sub ‘f’.

Nota:

Pentru ca f să fie o corespondență de la A la B:

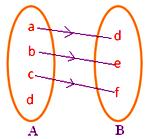
● Fiecare element din A trebuie să aibă imagine în B. Figura alăturată nu reprezintă o corespondență deoarece elementul d din ansamblul A nu este asociat cu nici un element din ansamblul B.

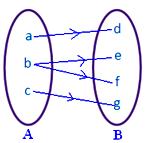
● Nici un element din A nu trebuie să aibă mai mult de o imagine. Figura alăturată nu reprezintă o corespondență, deoarece elementul b din ansamblul A este asociat cu două elemente d, f din ansamblul B.

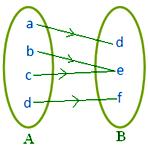
● Elemente diferite din A pot avea aceeași imagine în B. Figura alăturată reprezintă o cartografiere.

Nota:

Care cartografiere este o relație, dar orice relație poate să nu fie o cartografiere.

Funcția ca tip special de relație:

Să reamintim și să trecem în revistă funcția ca tip special de relație Să presupunem că, A și B sunt două seturi nevide, atunci o regulă „f” care asociază fiecare element din A cu un singur element din B se numește funcție sau o cartografiere din A în B.
Dacă ‘f’ este o corespondență de la A la B,

se exprimă prin f: A → B

se citește ca ‘f’ este o funcție de la A la B.
Dacă ‘f ‘ este o funcție de la A la B și x∈A și y∈B, atunci spunem că y este imaginea elementului x sub funcția ‘ f ‘ și o notăm cu f(x).
De aceea, o scriem ca y = f(x)

Aici, elementul x se numește preimaginea lui y.

Atunci, pentru o funcție de la A la B.
● A și B trebuie să fie nevidă.

● Fiecare element din A trebuie să aibă imagine în B.

● Niciun element din „A” nu trebuie să aibă mai mult de o imagine în „B”.
Nota:

● Două sau mai multe elemente din A pot avea aceeași imagine în B.

● f : x → y înseamnă că, sub funcția ‘f’ din A în B, un element x din A are imaginea y în B.

● Este necesar ca fiecare imagine f să fie în B, dar pot exista unele elemente în B care nu sunt imagini f ale niciunui element din A.

● Relații și corespondențe

Pareche ordonată

Produs cartezian a două ansambluri

Relație

Domeniul și domeniul unei relații

Funcții sau corespondențe

Domeniu Co-.domeniul și domeniul de acțiune al unei funcții

● Relații și mape – Fișe de lucru

Față de lucru cu relații matematice

Față de lucru cu funcții sau mape

.

Probleme de matematică de clasa a VII-a

Practică de matematică de clasa a VIII-a
De la Funcții sau Mapare la PAGINA DE ACASĂ