Circumferința unui cerc – Explicație și exemple

Am văzut mai înainte cum se găsește perimetrul poligonului. Știm că cercul nu este un poligon, prin urmare, nu ar trebui să aibă un perimetru. Folosim o formă echivalentă pentru un cerc, numită circumferință.

În acest articol, vom discuta despre cum să găsim circumferința unui cerc, formula circumferinței unui cerc și exemple de probleme despre circumferința unui cerc.

Ce este circumferința unui cerc?

Distanța în jurul unui poligon, cum ar fi un pătrat sau un dreptunghi, se numește perimetru (P). Pe de altă parte, distanța din jurul unui cerc se numește circumferință (C). Prin urmare, circumferința unui cerc este distanța liniară a unei muchii a cercului.

De ce avem nevoie să calculăm circumferința unui cerc?

Căutarea circumferinței unui obiect este importantă în următoarele scenarii:

Dacă doriți să cumpărați un sutien, un pantalon sau un pulover, trebuie să știți distanța din jurul taliei sau pieptului. Deși corpul dvs. nu este un cerc perfect, va trebui să îi măsurați circumferința folosind o bandă de măsură. Croitorii folosesc mai ales această tehnică pentru a determina circumferința unei rochii.

De asemenea, trebuie să cunoașteți circumferința unui cerc atunci când faceți lucrări de artizanat, când puneți garduri în jurul căzii dvs. cu hidromasaj sau pur și simplu rezolvați o problemă de matematică pentru școală.

Cum se găsește circumferința unui cerc?

După cum s-a spus mai devreme, perimetrul sau circumferința unui cerc este distanța din jurul unui cerc sau a oricărei forme circulare. Circumferința unui cerc este aceeași cu lungimea unei linii drepte care este pliată sau îndoită pentru a forma cercul. Circumferința unui cerc se măsoară în metri, kilometri, yarzi, inci etc.

Există două moduri de a afla perimetrul sau circumferința unui cerc. Prima formulă presupune utilizarea razei, iar a doua presupune utilizarea diametrului unui cerc. Este important de reținut că, ambele metode dau același rezultat.

Să aruncăm o privire.

Circumferința unui cerc este dată de;

C = 2 * π* R = 2πR

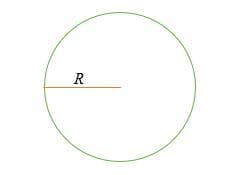
unde,

C = Circumferința sau perimetrul,

R = raza unui cerc,

π = constanta matematică cunoscută sub numele de Pi

sau

C = π* D = π D

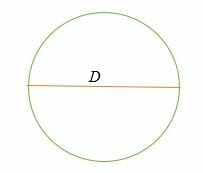
unde, D = 2R = Diametrul unui cerc

Pentru orice cerc, raportul dintre circumferința sa și diametrul său este egal cu o constantă cunoscută sub numele de pi.

Circumferința/Diametru = Pi

C /D = Pi sau C/2R = pi

Valoarea aproximativă a lui pi (π) = 22/7 = 3,141515926535897…. (o valoare neterminală)

Pentru a calcula mai ușor circumferința unui cerc, se consideră că valoarea lui pi este 3,14 (π = 3,14).

Să vedem câteva exemple mai jos pentru a șlefui conceptul de circumferință.

Exemplul 1

Găsește circumferința cercului cu raza de 8 cm.

Soluția

Circumferința = 2 * π* R = 2πR

= 2 * 3,14 * 8

= 50,24 cm.

Exemplul 2

Calculați circumferința unui cerc al cărui diametru este de 70 mm

Soluția

Circumferința = π* D = π D

= 3,14 * 70

= 219.8 mm

Exemplu 3

Calculați perimetrul unei grădini de flori circulare a cărei rază este de 10 m.

Soluție

Circumferința = 2 * π* R = 2πR

= 2 * 3,14 * 10

= 62,8 m.

Exemplul 4

Circumferința unui cerc este de 440 m. Găsiți diametrul și raza cercului.

Soluție

Circumferința = 2 * π* R = 2πR

440 =2 * 3,14 * R

440 = 6.28R

Divizați ambele părți cu 6,28 pentru a obține,

R = 70,06

Din acest motiv, raza cercului este de 70,06 yarzi. Dar, deoarece diametrul este de două ori raza unui cerc, atunci, diametrul este egal cu 140,12 yarzi.

Exemplul 5

Diametrul roților unei biciclete este de 100 cm. Câte rotații va face fiecare roată pentru a parcurge o distanță de 157 metri

Soluție

Calculați circumferința roții bicicletei.

Circumferința = π D

= 3.14 * 100

= 314 cm

Pentru a obține numărul de rotații ale roții, împărțim distanța parcursă la circumferința roții.

Trebuie să convertim 157 de metri în cm înainte de a împărți, așa că înmulțim 157 cu 100 pentru a obține 15700 cm. Prin urmare,

Numărul de rotații = 15700 cm/314 cm

= 50 de rotații.

Exemplul 6

O bucată de sârmă sub forma unui dreptunghi cu lungimea de 100 cm și lățimea de 50 cm este tăiată și pliată pentru a face un cerc. Calculați circumferința și raza cercului format.

Soluție

Circumferința cercului format = perimetrul sârmei dreptunghiulare.

Perimetrul unui dreptunghi = 2(L + l)

= 2(100 + 50) cm

= 2 * 150 cm

= 300 cm.

Prin urmare, circumferința cercului va fi de 300 cm.

Calculați acum raza acestuia.

Circumferința = 2 π R

300 cm = 2 * π * R

300 cm = 2 * 3,14 * R

300 cm = 6,28R

Divizați ambele părți cu 6,28.

R = 47.77 cm

Deci, raza cercului va fi 47,77 cm.

Exemplul 7

Raza fiecărei roți a unei motociclete este de 0. 85 m. Cât de departe se va deplasa motocicleta dacă fiecare roată face 1000 de rotații. Să presupunem că motocicleta se deplasează pe o linie dreaptă.

Soluție

În primul rând, găsiți circumferința roții.

Circumferința = 2 π R

= 2 * 3,14 * 0,85

= 5,338 m.

Pentru a afla distanța parcursă, înmulțiți circumferința roții cu numărul de rotații efectuate.

Distanța = 5,338 * 1000

= 5338 m

Din acest motiv, distanța parcursă este egală cu 5,338 kilometri.

Întrebări practice

1. O pizza de 12 inci este servită lui Mike și prietenilor săi. Mike este interesat să calculeze circumferința acesteia. Ajutați-l!
2. Perimetrul unui anumit pătrat este 1/3 din aria unui anumit cerc. Dacă lungimea pătratului este de L unități, determinați diametrul cercului în funcție de L.

Răspunsuri

1. 12π inci sau 37,67 inci
2. 12L/π unități

Previous Lesson | Main Page | Next Lesson

.