Ce se întâmplă dacă datele dumneavoastră NU sunt normale?
On ianuarie 15, 2022 by adminÎn acest articol, discutăm despre limita lui Chebyshev pentru analiza statistică a datelor. În absența oricărei idei despre Normalitatea unui anumit set de date, această limită poate fi utilizată pentru a evalua concentrația datelor în jurul mediei.
Introducere
Este săptămâna Halloween, iar între trucuri și dulciuri, noi, tocilarii de date, râdem de acest meme drăguț pe rețelele de socializare.

Crezi că este o glumă? Permiteți-mi să vă spun că nu este o chestiune de râs. Este înfricoșătoare, fidelă spiritului de Halloween!
Dacă nu putem presupune că majoritatea datelor noastre (de origine comercială, socială, economică sau științifică) sunt cel puțin aproximativ „normale” (adică sunt generate de un proces gaussian sau de o sumă de mai multe astfel de procese), atunci suntem condamnați!
Iată o listă extrem de scurtă a lucrurilor care nu vor fi valabile,
- Întregul concept de six-sigma
- Faimoasa regulă 68-95-99,7
- Conceptul „sfânt” de p=0,05 (provine din intervalul 2 sigma) în analiza statistică
Suficient de înfricoșător? Haideți să vorbim mai mult despre asta…
Omnipotenta și omniprezenta distribuție normală
Să păstrăm această secțiune scurtă și dulce.
Distribuția normală (gaussiană) este cea mai cunoscută distribuție de probabilitate. Iată câteva link-uri către articolele care descriu puterea și aplicabilitatea sa largă,
- De ce oamenii de știință din domeniul datelor iubesc Gaussian
- Cum să dominați partea de statistică a interviului dvs. pentru știința datelor
- Ce este atât de important la distribuția normală?
Din cauza apariției sale în diverse domenii și a Teoremei Limitei Centrale (CLT), această distribuție ocupă un loc central în știința datelor și în analiză.
Atunci, care este problema?
Acestea sunt toate bune și frumoase, care este problema?
Problema este că adesea puteți găsi o distribuție pentru setul dvs. specific de date, care poate să nu satisfacă normalitatea, adică proprietățile unei distribuții normale. Dar, din cauza dependenței excesive de ipoteza Normalității, majoritatea cadrelor de analiză a afacerilor sunt adaptate pentru a lucra cu seturi de date distribuite normal.
Este aproape înrădăcinată în subconștientul nostru.
Să spunem că vi se cere să verificați dacă un nou lot de date dintr-un anumit proces (de inginerie sau de afaceri) are sens. Prin „a avea sens”, vă referiți dacă noile date aparțin, adică dacă se încadrează în „intervalul așteptat”.
Ce este această „așteptare”? Cum să cuantificăm intervalul?
Automat, ca și cum am fi dirijați de un impuls subconștient, măsurăm media și abaterea standard a eșantionului de date și procedăm la verificarea dacă noile date se încadrează în anumite intervale de abateri standard.
Dacă trebuie să lucrăm cu o limită de încredere de 95%, atunci suntem fericiți să vedem că datele se încadrează în 2 abateri standard. Dacă avem nevoie de o limită mai strictă, verificăm 3 sau 4 deviații standard. Calculăm Cpk, sau urmăm liniile directoare six-sigma pentru nivelul de calitate ppm (părți pe milion).
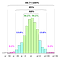
Toate aceste calcule se bazează pe presupunerea implicită că datele populației (NU ale eșantionului) urmează distribuția gaussiană i.adică procesul fundamental, din care au fost generate toate datele (în trecut și în prezent), este guvernat de modelul din partea stângă.
Dar ce se întâmplă dacă datele urmează tiparul din partea dreaptă?
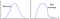
Orice, asta, și… aia?
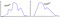
Există o limită mai universală atunci când datele NU sunt normale?
În cele din urmă, vom avea în continuare nevoie de o tehnică matematică solidă pentru a cuantifica limita noastră de încredere, chiar dacă datele nu sunt normale. Asta înseamnă că, calculul nostru se poate schimba puțin, dar ar trebui să putem spune în continuare ceva de genul acesta-
„Probabilitatea de a observa un nou punct de date la o anumită distanță față de medie este așa și așa…”
Evident, trebuie să căutăm o limită mai universală decât prețioasele limite gaussiene de 68-95-99.7 (corespunzătoare distanței de 1/2/3 deviații standard față de medie).
Din fericire, există o astfel de limită numită „Chebyshev Bound”.
Ce este Chebyshev Bound și cum este ea utilă?
Inegalitatea lui Chebyshev (numită și inegalitatea Bienaymé-Chebyshev) garantează că, pentru o clasă largă de distribuții de probabilitate, nu mai mult de o anumită fracțiune de valori pot fi mai mult decât o anumită distanță față de medie.
În mod specific, nu mai mult de 1/k² din valorile distribuției pot fi la o distanță mai mare de k abateri standard față de medie (sau, în mod echivalent, cel puțin 1-1/k² din valorile distribuției se află în interiorul a k abateri standard față de medie).
Se aplică la tipuri practic nelimitate de distribuții de probabilitate și funcționează pe o ipoteză mult mai relaxată decât Normalitatea.
Cum funcționează?
Chiar dacă nu știți nimic despre procesul secret din spatele datelor dumneavoastră, există o șansă bună să puteți spune următoarele,
„Am încredere că 75% din toate datele ar trebui să se încadreze în 2 deviații standard de la medie”,
Sau,
Am încredere că 89% din toate datele ar trebui să se încadreze în 3 deviații standard de la medie”.
Iată cum arată pentru o distribuție cu aspect arbitrar,

Cum se aplică?
După cum puteți ghici până acum, mecanismul de bază al analizei datelor dvs. nu trebuie să se schimbe câtuși de puțin. Veți aduna în continuare un eșantion de date (cu cât mai mare, cu atât mai bine), veți calcula aceleași două mărimi pe care sunteți obișnuiți să le calculați – media și abaterea standard, iar apoi veți aplica noile limite în locul regulii 68-95-99,7.

Tabloul arată astfel (aici k denotă atâtea abateri standard de la medie),

O demonstrație video a aplicației sale este aici,
Care este capcana? De ce nu folosesc oamenii această legătură „mai universală”?
Este evident care este capcana dacă ne uităm la tabel sau la definiția matematică. Regula lui Chebyshev este mult mai slabă decât regula gaussiană în ceea ce privește punerea de limite pe date.
Ea urmează un tipar 1/k² față de un tipar exponențial descrescător pentru distribuția normală.
De exemplu, pentru a delimita ceva cu un grad de încredere de 95%, trebuie să includeți date până la 4,5 deviații standard față de 4,5 deviații standard față de 4,5 deviații standard. doar 2 abateri standard (pentru Normal).
Dar poate totuși să salveze situația atunci când datele nu seamănă deloc cu o distribuție Normală.
Există ceva mai bun?
Există o altă limită numită, „Chernoff Bound”/ inegalitatea Hoeffding care oferă o distribuție cu coadă exponențial de ascuțită (în comparație cu 1/k²) pentru sume de variabile aleatoare independente.
Aceasta poate fi, de asemenea, utilizată în locul distribuției gaussiene atunci când datele nu par normale, dar numai atunci când avem un grad ridicat de încredere că procesul subiacent este compus din subprocese care sunt complet independente unele de altele.
Din păcate, în multe cazuri sociale și de afaceri, datele finale sunt rezultatul unei interacțiuni extrem de complicate a mai multor subprocese care pot avea o puternică interdependență.
Summary
În acest articol, am aflat despre un anumit tip de legătură statistică care poate fi aplicată la cea mai largă distribuție posibilă de date, independent de ipoteza Normalității. Acest lucru vine la îndemână atunci când știm foarte puțin despre adevărata sursă a datelor și nu putem presupune că acestea urmează o distribuție gaussiană. Limita urmează o lege de putere în loc de o natură exponențială (precum cea gaussiană) și, prin urmare, este mai slabă. Dar este un instrument important pe care trebuie să-l aveți în repertoriu pentru a analiza orice tip arbitrar de distribuție a datelor.
Lasă un răspuns