2.12: Ecuația lui Van der Waals

O ecuație datorată lui Van der Waals extinde ecuația gazului ideal într-un mod simplu. Ecuația lui Van der Waals este

\

Se potrivește mai bine cu datele de presiune-volum-temperatură pentru un gaz real decât o face ecuația gazului ideal. Ajustarea îmbunătățită se obține prin introducerea a doi parametri (denumiți „\(a\)” și „\(b\)”) care trebuie determinați experimental pentru fiecare gaz. Ecuația lui Van der Waals este deosebit de utilă în efortul nostru de a înțelege comportamentul gazelor reale, deoarece întruchipează o imagine fizică simplă pentru diferența dintre un gaz real și un gaz ideal.

În derivarea legii lui Boyle din legile lui Newton, presupunem că moleculele de gaz nu interacționează între ele. Argumente simple arată că acest lucru poate fi doar aproximativ adevărat. Moleculele reale de gaz trebuie să interacționeze unele cu altele. La distanțe scurte, ele se resping între ele. La distanțe ceva mai mari, ele se atrag între ele. Ecuația gazului ideal poate fi, de asemenea, derivată din ipotezele de bază pe care le-am formulat în §10 printr-o aplicare a teoriei termodinamicii statistice. Făcând diferite ipoteze despre proprietățile moleculare, putem aplica termodinamica statistică pentru a deriva\({}^{5}\) ecuația lui van der Waals. Ipotezele necesare sunt că moleculele ocupă un volum finit și că ele se atrag reciproc cu o forță care variază ca inversul unei puteri a distanței dintre ele. (Forța de atracție este de obicei presupusă a fi proporțională cu \(r^{-6}\).)

Pentru a recunoaște că moleculele de gaz reale se atrag și se resping reciproc, trebuie doar să ne amintim că orice gaz poate fi lichefiat prin reducerea temperaturii și creșterea presiunii aplicate asupra sa. Dacă răcim lichidul în continuare, acesta îngheață și se transformă în solid. Acum, două caracteristici distinctive ale unui solid sunt faptul că acesta își păstrează forma și că este aproape incompresibil. Atribuim incompresibilitatea unui solid forțelor de respingere dintre moleculele sale constitutive; acestea s-au apropiat atât de mult una de alta încât forțele de respingere dintre ele au devenit importante. Pentru a comprima solidul, moleculele trebuie să fie împinse și mai aproape una de alta, ceea ce necesită o forță exagerată. Pe de altă parte, dacă aruncăm un cub de gheață prin cameră, toate moleculele de apă care îl compun zboară împreună prin cameră. Evident, moleculele de apă din solid sunt atrase unele de altele, altfel ar merge fiecare pe drumuri diferite – aruncând cubul de gheață ar fi ca și cum ai arunca un pumn de nisip uscat. Dar moleculele de apă sunt aceleași molecule indiferent de temperatură sau de presiune, așa că, dacă există forțe de atracție și de respingere între ele în solid, aceste forțe trebuie să fie prezente și în fazele lichidă și gazoasă.

În faza gazoasă, moleculele sunt foarte depărtate; în faza lichidă sau solidă, ele sunt strânse împreună. La punctul de fierbere, volumul unui lichid este mult mai mic decât volumul gazului din care este condensat. La punctul de congelare, volumul unui solid este doar puțin diferit de volumul lichidului din care este congelat și este cu siguranță mai mare decât zero. Aceste observații banale sunt ușor de explicat presupunând că orice moleculă are un volum caracteristic. Putem înțelege că acest lucru este, la rândul său, o consecință a naturii forțelor intermoleculare; în mod evident, aceste forțe devin mai puternice pe măsură ce distanța dintre o pereche de molecule scade. Deoarece un lichid sau un solid ocupă un volum determinat, forța de respingere trebuie să crească mai rapid decât forța de atracție atunci când distanța intermoleculară este mică. Adesea este util să vorbim despre volumul molar al unei faze condensate. Prin volum molar se înțelege volumul unui mol dintr-o substanță pură. Volumul molar al unei faze condensate este determinat de distanța intermoleculară la care există un echilibru între forțele intermoleculare de atracție și de respingere.

Evident, moleculele sunt foarte apropiate unele de altele în fazele condensate. Dacă presupunem că spațiile goale dintre molecule sunt neglijabile, volumul unei faze condensate este aproximativ egal cu numărul de molecule din eșantion înmulțit cu volumul unei singure molecule. Atunci volumul molar este numărul lui Avogadro înmulțit cu volumul ocupat de o moleculă. Dacă cunoaștem densitatea, D, și masa molară, \(\suprafață{M}\), putem afla volumul molar, \(\suprafață{V}\), ca

\

Volumul ocupat de o moleculă, V\({}_{moleculă}\), devine

\

Presiunea și volumul care apar în ecuația lui van der Waals sunt presiunea și volumul gazului real. Putem corela termenii din ecuația lui van der Waals cu ecuația gazului ideal: Este util să ne gândim la termenii \(\left(P+{{an}^2}/{V^2}\right)\) și \(\left(V-nb\right)\) ca fiind presiunea și volumul unui gaz ideal ipotetic. Adică

\ &=nRT \end{align*}\]

Atunci avem

\

Derivăm ecuația gazului ideal dintr-un model în care moleculele sunt mase punctiforme care nu interacționează între ele. Așadar, volumul unui gaz ideal este volumul ocupat de un gaz ale cărui molecule individuale au volum zero. Dacă moleculele individuale ale unui gaz real ocupă efectiv un volum \({b}/{\overline{N}}\), atunci \(n\) moli din ele ocupă efectiv un volum

\

Ecuația lui Van der Waals spune că volumul unui gaz real este volumul care ar fi ocupat de masele punctiforme care nu interacționează, \(V_{gazul ideal}\), plus volumul efectiv al moleculelor de gaz în sine. (Atunci când datele referitoare la moleculele gazului real sunt adaptate la ecuația lui van der Waals, valoarea lui \(b\) este, de obicei, ceva mai mare decât volumul estimat din densitatea lichidului și din greutatea moleculară. Vezi problema 24.)

În mod similar, avem

\

Potem înțelege acest lucru ca o consecință logică a interacțiunilor atractive dintre moleculele gazului real. Cu \(a>0\), se spune că presiunea gazului real este mai mică decât presiunea gazului ideal ipotetic, cu o cantitate care este proporțională cu \({\left({n}/{V}\right)}^2\). Constanta de proporționalitate este \(a\). Deoarece \({n}/{V}\) este densitatea molară (moli pe unitatea de volum) a moleculelor de gaz, aceasta este o măsură a concentrației. Numărul de ciocniri între molecule de același tip este proporțional cu pătratul concentrației lor. (Vom analiza acest aspect mai în detaliu în capitolele 4 și 5.) Așadar, \({\left({n}/{V}\right)}^2\) este o măsură a frecvenței cu care moleculele reale de gaz intră în contact strâns unele cu altele. Dacă acestea se atrag reciproc atunci când se apropie una de cealaltă, efectul acestei atracții ar trebui să fie proporțional cu \({\left({n}/{V}\right)}^2\). Deci ecuația lui van der Waals este în concordanță cu ideea că presiunea unui gaz real este diferită de presiunea gazului ideal ipotetic cu o cantitate care este proporțională cu frecvența și puterea interacțiunilor atractive.

Dar de ce ar trebui ca interacțiunile atractive să aibă acest efect; de ce ar trebui ca presiunea gazului real să fie mai mică decât cea a gazului ideal ipotetic? Poate că cel mai bun mod de a dezvolta o imagine calitativă este să recunoaștem că forțele intermoleculare atractive tind să determine moleculele de gaz să se aglomereze. La urma urmei, aceste forțe atractiveforța atractivă este cea care determină moleculele să se agregheze într-un lichid la temperaturi scăzute. Deasupra punctului de fierbere, capacitatea moleculelor de gaz de a merge pe drumuri separate limitează efectele acestei tendințe; cu toate acestea, chiar și în gaz, forțele atractive trebuie să acționeze într-un mod care tinde să reducă volumul ocupat de molecule. Deoarece volumul ocupat de gaz este dictat de mărimea recipientului – și nu de proprietățile gazului în sine – această tendință de aglomerare își găsește expresia ca o scădere a presiunii.

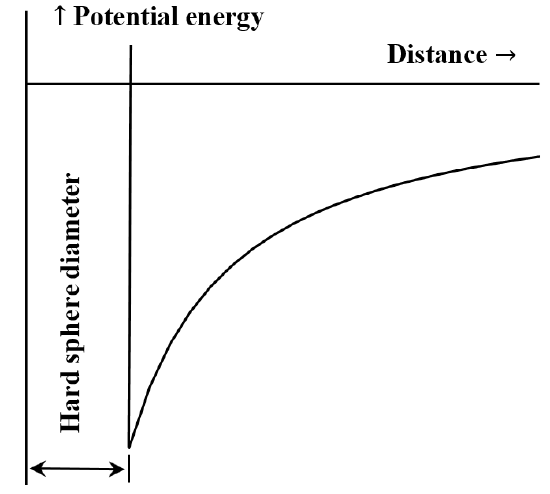
Este frecvent utilă descrierea interacțiunii dintre particule sau fracțiuni chimice în termenii unei diagrame de energie potențială în funcție de distanță. Ecuația lui van der Waals corespunde cazului în care interacțiunea repulsivă dintre molecule este inexistentă până când moleculele intră în contact. Odată ce acestea intră în contact, energia necesară pentru a le apropia și mai mult devine arbitrar de mare. Adesea, acest lucru este descris spunând că se comportă ca niște „sfere dure”. Forța de atracție dintre două molecule scade pe măsură ce distanța dintre ele crește. Atunci când acestea sunt foarte îndepărtate, interacțiunea atractivă este foarte mică. Spunem că energia de interacțiune este zero atunci când moleculele sunt infinit de îndepărtate. Dacă avem inițial două molecule foarte depărtate, staționare, care se atrag reciproc, acestea se vor deplasa spontan una spre cealaltă, câștigând energie cinetică pe măsură ce se deplasează. Energia lor potențială scade pe măsură ce se apropie una de cealaltă, atingând cea mai mică valoare atunci când moleculele intră în contact. Astfel, ecuația lui van der Waals implică diagrama energie potențială în funcție de distanță schițată în figura 5.

.