Articles

Suma Produktu (SOP) & Produkt Sumy (POS)

On 10 listopada, 2021 by admin

Produkt Sumy (POS) & Suma Produktu (SOP)

Suma Produktu (SOP)

Suma Produktu jest skróconą formą SOP. Suma iloczynu jest formą wyrażenia w algebrze Boole’a, w której różne warunki iloczynu danych wejściowych są sumowane razem. Ten produkt nie jest arytmetyczne mnożenie, ale to jest Boolean logiczne AND i Suma jest Boolean logiczne OR.

Aby lepiej zrozumieć o SOP, musimy wiedzieć o min term.

Min Term

Minterm oznacza termin, który jest prawdziwy dla minimalnej liczby kombinacji wejść. To jest prawdziwe tylko dla jednej kombinacji wejść.

Skoro bramka AND również daje True tylko wtedy, gdy wszystkie jej wejścia są prawdziwe, więc możemy powiedzieć, że min terminy są AND kombinacji wejść jak w tabeli poniżej.

3 wejścia mają 8 różnych kombinacji. Każda kombinacja ma min terms oznaczane przez małe m i jego dziesiętny numer kombinacji napisane w indeksie dolnym. Każdy z tych minterms będzie tylko prawdziwe dla określonej kombinacji input.

• Możesz również przeczytać: Cyfrowy licznik asynchroniczny (Ripple Counter) – rodzaje, działanie & Zastosowanie

Rodzaje form Sum Of Product (SOP)

Istnieje kilka różnych form Sum of Product.

• Kanoniczna Forma SOP
• Niekanoniczna Forma SOP
• Minimalna Forma SOP

Kanoniczna Forma SOP

Jest to standardowa forma Sumy Produktu. Jest on tworzony przez O Ring the minterms funkcji, dla której wyjście jest prawdziwe. Jest to również znane jako suma terminów Min lub kanoniczna disjunctive normal form (CDNF). Jest to tylko fantazyjna nazwa. „Kanoniczny” oznacza „znormalizowany”, a „disjunctive” oznacza „Logical OR union”.

Kanoniczne wyrażenie SOP jest reprezentowane przez znak sumowania ∑ i minterms w nawiasach klamrowych, dla których wyjście jest prawdziwe.

Na przykład, tabela prawdy funkcji jest podana poniżej.

Dla tej funkcji kanoniczne wyrażenie SOP to

F = ∑( m1, m2, m3, m5 )

Co oznacza, że funkcja jest prawdziwa dla min terminów {1, 2, 3, 5}.

Rozwijając sumowanie otrzymujemy.

F = m1 + m2 + m3 + m5

Teraz wstawiając wyrazy min do wyrażenia

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

Forma kanoniczna zawiera wszystkie wejścia zarówno dopełnione jak i nie dopełnione w swoich wyrazach iloczynowych.

Możesz też przeczytać: Cyfrowy licznik synchroniczny – typy, działanie & Zastosowania

Niekanoniczna forma SOP

Jak sama nazwa wskazuje, forma ta jest niestandardową formą wyrażeń SOP. Terminy iloczynowe nie są terminami min, ale są uproszczone. Weźmy powyższą funkcję w formie kanonicznej jako przykład.

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

F = A̅B̅C + A̅B(C̅ + C) + AB̅C

F = A̅B̅C + A̅B(1) + AB̅C

F = A̅B̅C + A̅B + AB̅C

To wyrażenie wciąż ma postać sumy iloczynów, ale jest to postać niekanoniczna lub niestandardowa forma.

Minimalna forma SOP

Ta forma jest najbardziej uproszczonym wyrażeniem SOP funkcji. Jest to również forma niekanoniczna. Minimalna forma SOP może być wykonana przy użyciu twierdzeń algebry Boole’a, ale jest bardzo łatwa do wykonania przy użyciu mapy Karnaugha (K-map).

Minimalna forma SOP jest preferowana, ponieważ wykorzystuje minimalną liczbę bramek i linii wejściowych. jest komercyjnie korzystna ze względu na jej kompaktowy rozmiar, dużą szybkość i niski koszt produkcji.

Przyjmijmy przykład funkcji podanej powyżej w postaci kanonicznej.

Jej K-mapa jest podana poniżej.

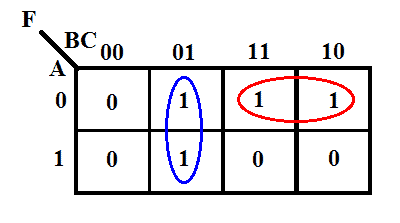
Zgodnie z mapą K, wyrażenie wyjściowe będzie

F = B̅C + A̅B

Jest to najbardziej uproszczone &zoptymalizowane wyrażenie dla wspomnianej funkcji. To wyrażenie wymaga tylko dwóch 2-wejściowych bramek AND &jednej 2-wejściowej bramki OR. Jednak forma kanoniczna wymaga czterech 3-wejściowych bramek AND & jednej 4-wejściowej bramki OR, co jest stosunkowo bardziej kosztowne niż implementacja formy minimalnej.

• Możesz również przeczytać: Licznik pierścieniowy & Licznik Johnsona – budowa &działanie

Schematic Design of Sum Of Product (SOP)

Wyrażenie SOP implementuje 2-poziomową konstrukcję AND-OR, w której bramka 1 poziomu jest bramką AND następującą po bramce 2 poziomu, która jest bramką OR. Schematyczny projekt wyrażenia SOP wymaga tablicy grup bramek AND & jednej bramki OR.

Każde wyrażenie SOP ma nieco taki sam projekt, tzn. wszystkie wejścia przechodzą przez bramkę AND, a następnie wyjście tych bramek AND przechodzi przez bramkę OR, jak pokazano na rysunku poniżej.

Liczba wejść i liczba bramek AND zależy od wyrażenia, które się implementuje.

Przykład konstrukcji kanonicznego i minimalnego wyrażenia SOP dla funkcji jest podany poniżej.

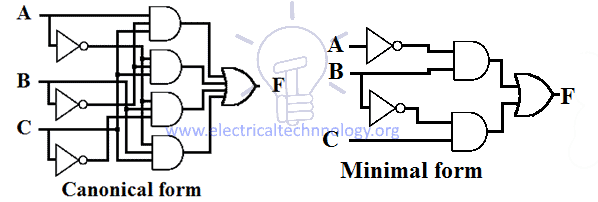
Konwersja z minimalnego SOP do kanonicznej formy SOP

Konwersja z minimalnej lub dowolnego rodzaju niekanonicznej formy do formy kanonicznej jest bardzo prosta.

Jak wiemy, forma kanoniczna ma min terminów & min terminów składa się ze wszystkich wejść albo uzupełnionych lub nieuzupełnionych. Tak więc każdy termin minimalnego SPO pomnożymy przez sumę brakującej formy uzupełnionej i nieuzupełnionej danych wejściowych. Przykład przekształcenia powyższej funkcji w minimalną postać SOP jest podany poniżej.

Minimalna postać SOP

F = A̅B + B̅C

Wyraz A̅B ma brakujące wejście C. Zatem pomnożymy A̅B przez (C+C̅), ponieważ (C+C̅ = 1). Określenie B̅C jest brakującym wejściem A. więc zostanie on pomnożony przez (A+A̅)

F = A̅B(C + C̅) + B̅C(A + A̅)

F = A̅BC + A̅BC̅ + AB̅C + A̅B̅C

Teraz to wyrażenie ma postać kanoniczną.

Konwersja z kanonicznego SOP do kanonicznego POS

Standardowe wyrażenie SOP można przekształcić w standardowe wyrażenie POS (iloczyn sum). Na przykład, funkcja podana powyżej ma postać kanonicznego SOP

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

F = ∑ ( m1, m2, m3, m5 )

Pozostałe wyrażenia tej funkcji są maksimami, dla których wyjściem jest fałsz. Te maksymalne wyrażenia to M0,M4,M6,M7. Te wyrażenia max będą użyte w wyrażeniu POS jako iloczyn tych wyrażeń max. Symbolem iloczynu jest ∏.

F = ∏ ( M0, M4, M6, M7)

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

Eksperymenty max są dopełnieniem mintermów. Czyli dlaczego M0=(A+B+C).

• Możesz też przeczytać: Ripple Carry And Carry Look Ahead Adder

Konwersja z kanonicznego SOP na minimalny SOP

Kanoniczny SOP można przekonwertować na minimalny SOP. Można go przekonwertować za pomocą mapy Karnaugha lub twierdzeń algebry Boole’a. Metoda K-map jest bardzo prosta i jej przykład został zrobiony powyżej w minimalnej formie SOP.

Produkt Sumy

Produkt Sumy skrótowo POS.

Forma produktu Sumy jest formą, w której produkty różnych terminów sumy wejść są brane. To nie są arytmetyczne iloczyn i suma, ale są to logiczne Boolean AND i OR odpowiednio.

Aby lepiej zrozumieć o produkcie sumy, musimy wiedzieć o Max term.

Max Term

Maxterm oznacza termin lub wyrażenie, które jest prawdziwe dla maksymalnej liczby kombinacji wejść lub które jest fałszywe tylko dla jednej kombinacji wejść.

Ponieważ bramka OR również daje false tylko dla jednej kombinacji wejść. Więc Maxterm jest OR albo uzupełnionych albo nieuzupełnionych wejść.

Max terms dla 3 zmiennych wejściowych są podane poniżej.

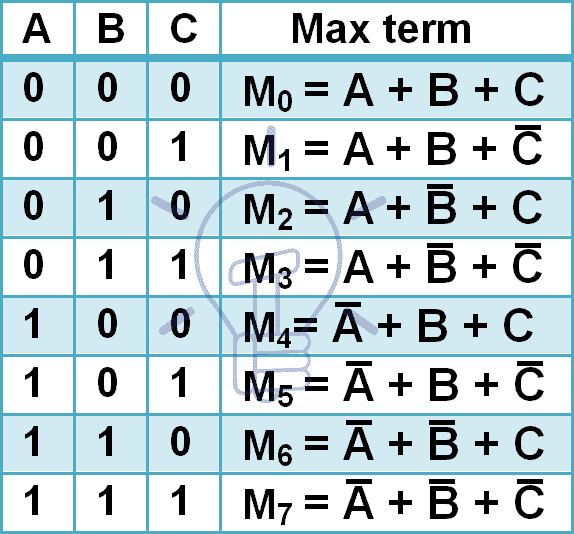
3 wejścia mają 8 różnych kombinacji więc będą miały 8 maxtermów. Maxtermy są oznaczane przez duże M i dziesiętny numer kombinacji w indeksie dolnym, jak pokazano w tabeli powyżej.

W maxterm, każde wejście jest uzupełnione, ponieważ maxterm daje '0′ tylko wtedy, gdy wspomniana kombinacja jest zastosowana i maxterm jest uzupełnieniem minterm.

M3 = m̅3

M3 = (A̅BC)’

M3 = A + B̅ +C̅ DE Prawo Morgana

Which is why for A=0 Max term consist A & for A=1 Max term consist A̅.

You may also read: Digital Flip-Flops – SR, D, JK and T Flip Flops

Typy form Product Of Sum

Istnieją różne typy form Product Of Sum.

• Kanoniczna forma POS
• Non – Canonical Form
• Minimal POS Form

Kanoniczna forma POS

Jest ona również znana jako Product of Max term lub Canonical conjunctive normal form (CCNF). Kanoniczny oznacza standardowy, a koniunkcyjny oznacza przecięcie.

W tej formie, Maxtermy są AND razem, dla których wyjście jest fałszywe.

Kanoniczne wyrażenie POS jest reprezentowane przez ∏ i Maxtermy, dla których wyjście jest fałszywe w nawiasach, jak pokazano w przykładzie poniżej.

F = ∏ (M0, M4, M6, M7)

Rozszerzenie iloczynu

F = M0.M4.M6.M7

Układanie terminów Max

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

Forma kanoniczna zawiera wszystkie wejścia albo uzupełnione albo nieuzupełnione w swoim każdym terminie Sumy.

• You may also read: Clap Switch Circuit Electronic Project Using 555 Timer

Non – Canonical Form

Iloczyn wyrażenia sumy, który nie jest w standardowej formie jest nazywany formą niekanoniczną.

Przyjmijmy wyżej podaną funkcję jako przykład.

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

F = (B+C) (A̅+B̅+C)(A̅+B̅+C̅)

Te same, ale odwrócone terminy eliminuje z dwóch terminów Max i tworzą pojedynczy termin, aby udowodnić to tutaj jest przykład.

= (A+B+C) (A̅+B+C)

= AA̅+AB+AC+A̅B+BB+BC+A̅C+BC+CC

= 0+AB+AC+A̅B+A̅C+B+B+C

= A(B+C)+A̅(B+C)+B(1+C)+C

= A(B+C)+A̅(B+C)+B(1+C)+C

= (B+C)(A+A̅)+B(1)+C

= (B+C)(0)+B+C

= B+C

Uzyskane wyrażenie ma nadal postać iloczynu sum, ale nie jest to postaćforma kanoniczna.

Minimalna forma POS

Jest to najbardziej uproszczona i zoptymalizowana forma wyrażenia POS, która jest niekanoniczna. Minimalna postać Product of Sum może być osiągnięta przy użyciu twierdzeń algebry Boole’a, jak w niekanonicznym przykładzie podanym powyżej. Inną metodą osiągnięcia minimalnej formy POS jest użycie mapy Karnaugha, która jest stosunkowo łatwiejsza niż użycie twierdzeń algebry Boole’a. Minimalna forma POS używa mniejszej liczby wejść i bramek logicznych podczas jej implementacji, dlatego są one preferowane w stosunku do formy kanonicznej za ich kompaktową, szybką i tanią implementację.

Przyjmijmy wyżej podaną funkcję jako przykład

K-mapa funkcji

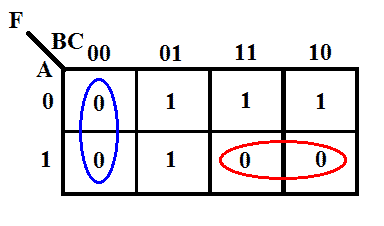
Minimalne wyrażenie przy użyciu K-mapy

F = (B+C) (A̅+B̅)

Osiągnięte wyrażenie jest minimalnym iloczynem postaci sumy. Jest to nadal Product of Sum expression, ale potrzebuje tylko 2 wejścia dwie bramki OR i pojedynczą 2 wejściową bramkę AND. Jednak forma kanoniczna potrzebuje 4 bramek OR o 3 wejściach i 1 bramki AND o 4 wejściach.

• You may also read: Układy wzmacniaczy z ujemnym sprzężeniem zwrotnym i ujemnym sprzężeniem zwrotnym

Schematyczna konstrukcja iloczynu sumy (POS)

Wyrażenie iloczynu sumy ma specyficzną schematyczną konstrukcję OR-AND. W OR-AND wejścia przechodzą przez tablicę bramek OR, która jest pierwszym poziomem bramek, wyjście z pierwszego poziomu bramek OR przechodzi przez drugi poziom bramek, który jest bramką AND.

Liczba wejść i liczba bramek używanych w tym projekcie zależy od wyrażenia, które ma być zaimplementowane.

Forma kanoniczna składa się z maksymalnej liczby możliwych wejść i bramek, natomiast forma minimalna składa się z najmniejszej możliwej liczby wejść i bramek. Schematyczna konstrukcja kanonicznej i minimalnej formy POS jest podana poniżej.

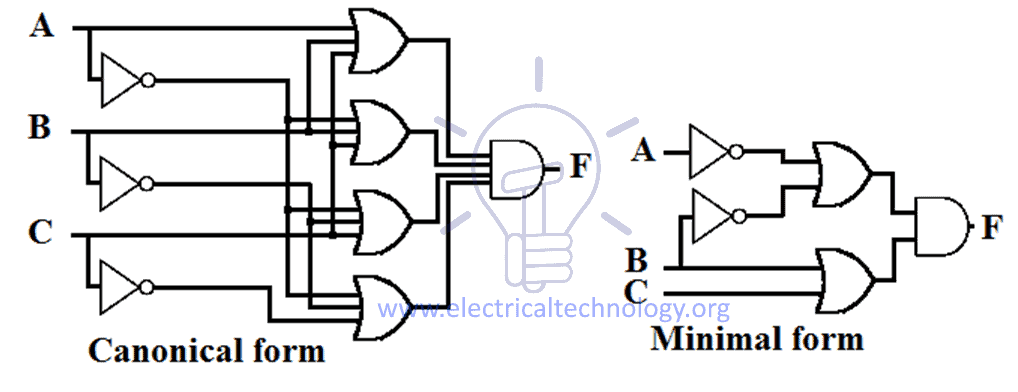
Konwersja z minimalnej formy POS do kanonicznej formy POS

Jak wiemy, kanoniczna forma POS ma max terminów i max terminów zawiera każde wejście albo uzupełnione albo nieuzupełnione. Tak więc dodamy każdy termin sumy z iloczynem uzupełnionych i nieuzupełnionych brakujących danych wejściowych. Przykład jego przekształcenia jest podany poniżej.

Minimalna postać POS

F = (A̅+B̅) (B+C)

(A̅+B̅) termin jest brakującym wejściem C, więc dodamy do niego (CC̅). (B+C) terminowi brakuje wejścia A, więc dodamy do niego (AA̅).

F = (A̅+B̅+CC̅) (B+C+AA̅)

F = (A̅+B̅+C)(A̅+B̅+C̅)(A+B+C)(A̅+B+C)

Ten wyraz jest teraz w postaci kanonicznej.

• Możesz też przeczytać: Licznik i rodzaje liczników elektronicznych

Konwersja z POS kanonicznego na SOP

Iloczyn wyrażenia Suma może być przekonwertowany na postać Suma produktu tylko wtedy, gdy wyrażenie jest w postaci kanonicznej. Kanoniczne POS i kanoniczne SOP są wzajemnie konwertowalne, tzn. mogą być konwertowane na siebie nawzajem. Przykład konwersji POS na SOP jest podany poniżej.

Forma kanoniczna POS

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

W formie kanonicznej każdy termin sumy jest terminem maksymalnym, więc można ją również zapisać jako:

F = ∏(M0,M4,M6,M7)

Pozostałe kombinacje wejść są minterminami funkcji, dla których jej wyjście jest prawdziwe. Aby przekształcić je na wyrażenie SOP, najpierw zmienimy symbol na sumowanie (∑) i użyjemy pozostałych mintermów.

F = ∑ (m1,m2,m3,m5)

Teraz rozwiniemy znak sumowania, aby utworzyć kanoniczne wyrażenie SOP.

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

Wyrażenia Min są dopełnieniem wyrażeń Max dla tej samej kombinacji wejść.

Canonical to Minimal POS

Kanoniczne wyrażenie Product of Sum może być przekształcone w Minimal Product of Sum za pomocą mapy Karnaugha (K-map). Inną metodą konwersji kanonicznego na minimalny jest użycie algebraicznych twierdzeń Boole’a.

Użycie mapy K jest bardzo łatwe, dlatego mapa K jest preferowana. Dla minimalnego wyrażenia POS, 0’s w K-map są łączone w grupy i wyrażenie, które otrzymujemy jest uzupełnione, ponieważ grupy zostały wykonane z '0’s. Jego przykład został wykonany powyżej.

Możesz również przeczytać:

• Digital Logic NOT Gate – Digital Inverter Logic Gate
• Exclusive-NOR (XNOR) Digital Logic Gate
• Digital Logic NOR Gate
• Digital Logic NAND Gate

.