Rozkład dochodu

Definiowanie i mierzenie dystrybucji dochodu

Rozkład dochodu to gładkość lub równość, z jaką dochód jest rozdawany wśród członków społeczeństwa. Jeśli każdy zarabia dokładnie tyle samo pieniędzy, wtedy dystrybucja dochodu jest idealnie równa. Jeśli nikt nie zarabia żadnych pieniędzy z wyjątkiem jednej osoby, która zarabia wszystkie pieniądze, wtedy dystrybucja dochodu jest idealnie nierówna. Zazwyczaj jednak dystrybucja dochodu w społeczeństwie mieści się gdzieś pośrodku między równością a nierównością.

Jak mierzymy ten stopień równości lub nierówności? Ekonomiści często mierzą równość dochodów mierząc, ile dochodu uzyskują różne segmenty populacji. Na przykład, jeśli podzielimy wszystkich pracowników na pięć segmentów pod względem tego, ile pieniędzy zarabiają: górne 20%, drugie 20%, trzecie 20%, czwarte 20% i dolne 20%, i uzyskamy dane na temat tego, ile pieniędzy zarabiają, możemy następnie stworzyć wykres wyszczególniający, ile dochodu zarabia każdy segment z całkowitej kwoty dochodu wszystkich pracowników. Im większa jest różnica między poszczególnymi segmentami, tym większa jest nierówność dochodów.

Powiedzmy, że średnie dochody dla pięciu segmentów w społeczeństwie są $ 10,000, $ 24,000, $ 50,000, $ 80,000 i $ 110,000. Aby przyjrzeć się dystrybucji dochodu, musimy zobaczyć, jaki procent całkowitego dochodu osiąga każdy segment, a nie faktyczną ilość pieniędzy, które każdy z nich zarabia. Ponieważ każdy z segmentów jest równy pod względem wielkości, nie musimy się martwić o ważenie średnich dochodów i możemy wykonać prostą kalkulację zarobków każdego segmentu.

Dla całkowitego dochodu użyjemy sumy pięciu średnich dochodów:

Dochód całkowity = 10000 + 24000 + 50000 + 80000 + 110000
Dochód całkowity = 274000

Następnie znajdujemy procent całkowitego dochodu, jaki zarabia każdy segment populacji, dzieląc jego dochód przez całkowity dochód:

Procent segmentu dolnego = 10000/274000 = 0.036 = 3.6%
Drugi segment procent = 24000/274000 = 0.088 = 8.8%
Trzeci segment procentowy = 50000/274000 = 0.182 = 18.2%
Czwarty segment procentowy = 80000/274000 = 0.292 = 29.2%
Górny segment procentowy = 110000/274000 = 0.401 = 40.1%

Co te liczby wskazują jest to, że dolna piąta część populacji dostaje mniej niż 4% całkowitego dochodu, podczas gdy górna piąta część populacji dostaje ponad 40% całkowitego dochodu, wskazując na duży stopień nierówności dochodów.

Ekonomiści patrzą również na łączne dane dotyczące dystrybucji dochodu. Aby to zrobić, wystarczy dodać procenty razem na każdym poziomie, dając kwotę dochodu uzyskanego przez wszystkich ludzi na lub poniżej pewnego poziomu. W naszym przykładzie działałoby to w następujący sposób:

Segment dolny skumulowany procent = 3,6%
Segment drugi skumulowany procent = 3,6% + 8,8% = 12,4%
Segment trzeci skumulowany procent = 12,4% + 18,2% = 30,6%
Segment czwarty skumulowany procent = 30.6% + 29,2% = 59,8%
Odsetek skumulowany segmentu górnego = 59,8% + 40,1% = 99,9%

Zauważ, że całkowity procent skumulowany, który powinien być równy 100%, ponieważ reprezentuje całkowity dochód uzyskany przez wszystkich pracowników, wynosi tylko 99,9%. To czasami zdarza się z powodu zaokrąglania liczb.

Te dwie liczby, procent i procent skumulowany, są zwykle umieszczane w tabeli dla łatwiejszego odczytu:

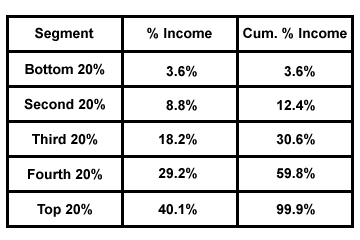
Krzywe Lorenza i współczynniki Giniego

Pomimo że dane dotyczące procentu i skumulowanego procentu mogą dać przybliżone pojęcie o tym, jak równa lub nierówna jest dystrybucja dochodu, czasami łatwiej jest zobaczyć, jak układają się one na wykresie, tak abyśmy mogli uzyskać wizualne poczucie równości dochodu. Aby to zrobić, wykreśl ile zarabia każdy z segmentów populacji (narastająco) i porównaj otrzymaną krzywą z idealnie równym rozkładem dochodów, który byłby wykresem prostoliniowym:

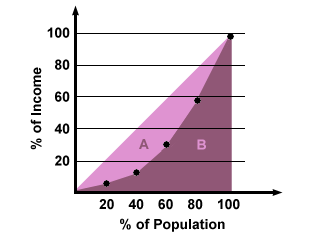
Ten typ wykresu, przedstawiający rozkład dochodów pomiędzy segmentami populacji, nazywamy krzywą Lorenza. Korzystając z krzywej Lorenza, możemy również wygenerować liczbową reprezentację równości dochodów, zwaną współczynnikiem Giniego. Współczynnik Giniego, mieszczący się w przedziale od 0 do 1, jest równy obszarowi pomiędzy krzywą rzeczywistą a krzywą równego podziału podzielonemu przez całkowity obszar pod krzywą równego podziału. Na powyższym rysunku, współczynnik Giniego jest równy powierzchni A podzielonej przez powierzchnię (A + B). Im większy jest współczynnik Giniego, tym większy jest stopień nierówności dochodów. Idealnie równy podział dochodu będzie miał współczynnik Giniego równy 0, podczas gdy idealnie nierówny podział będzie miał współczynnik Giniego równy 1.

Mobilność dochodu

Kolejnym czynnikiem do rozważenia przy badaniu stopnia nierówności w społeczeństwie jest wielkość mobilności dochodu. Mobilność dochodów odnosi się do łatwości, z jaką pracownicy mogą poruszać się w górę i w dół w hierarchii siły zarobkowej. Jeśli bogaci zawsze pozostają bogaci, a biedni zawsze pozostają biedni, to nierówna dystrybucja dochodów jest stałym i poważnym problemem. Jeśli jednak pracownicy z łatwością przechodzą z klasy średniej do klasy wyższej lub z klasy niższej do średniej, stopień nierówności staje się mniej poważny, ponieważ nierówności są płynne i tymczasowe (na poziomie indywidualnym).

.