Research Methods in Psychology

Co to są badania korelacyjne?

Badania korelacyjne to rodzaj badań nieeksperymentalnych, w których badacz mierzy dwie zmienne (binarne lub ciągłe) i ocenia związek statystyczny (tj., Korelacja) pomiędzy nimi przy niewielkim lub żadnym wysiłku w celu kontroli zmiennych zewnętrznych. Istnieje wiele powodów, dla których badacze zainteresowani statystycznymi związkami między zmiennymi decydują się na przeprowadzenie badania korelacyjnego zamiast eksperymentu. Pierwszym z nich jest to, że nie wierzą oni, iż statystyczny związek jest związkiem przyczynowym lub nie są zainteresowani związkami przyczynowymi. Przypomnijmy, że dwa cele nauki to opisywanie i przewidywanie, a strategia badań korelacyjnych pozwala badaczom osiągnąć oba te cele. W szczególności, ta strategia może być użyta do opisania siły i kierunku związku pomiędzy dwiema zmiennymi i jeśli istnieje związek pomiędzy zmiennymi, wtedy badacze mogą użyć wyników jednej zmiennej do przewidywania wyników drugiej (używając techniki statystycznej zwanej regresją, która jest omówiona bardziej szczegółowo w sekcji na temat Korelacji Złożonej w tym rozdziale).

Innym powodem, dla którego badacze wybierają badanie korelacyjne zamiast eksperymentu, jest to, że statystyczny związek zainteresowania jest uważany za przyczynowy, ale badacz nie może manipulować zmienną niezależną, ponieważ jest to niemożliwe, niepraktyczne lub nieetyczne. Na przykład, choć badacz może być zainteresowany związkiem między częstotliwością używania marihuany a zdolnościami pamięciowymi, nie może etycznie manipulować częstotliwością, z jaką ludzie używają marihuany. Jako taki, musi polegać na strategii badań korelacyjnych; musi po prostu zmierzyć częstotliwość, z jaką ludzie używają marihuany i zmierzyć ich zdolności pamięciowe za pomocą standaryzowanego testu pamięci, a następnie określić, czy częstotliwość, z jaką ludzie używają marihuany, jest statystycznie związana z wynikami testu pamięci.

Korelacja jest również używana do ustalenia wiarygodności i ważności pomiarów. Na przykład, badacz może ocenić ważność krótkiego testu ekstrawersji, podając go dużej grupie uczestników wraz z dłuższym testem ekstrawersji, którego ważność została już wykazana. Badacz ten może następnie sprawdzić, czy wyniki uczestników w krótkim teście są silnie skorelowane z ich wynikami w dłuższym teście. Uważa się, że żaden z wyników testu nie powoduje drugiego, więc nie ma tu zmiennej niezależnej, którą można by manipulować. W rzeczywistości, terminy zmienna niezależna i zmienna zależna nie mają zastosowania do tego rodzaju badań.

Inną mocną stroną badań korelacyjnych jest to, że są one często bardziej wiarygodne zewnętrznie niż badania eksperymentalne. Przypomnijmy, że zazwyczaj istnieje kompromis pomiędzy wiarygodnością wewnętrzną a zewnętrzną. Gdy do eksperymentów dodaje się więcej kontroli, zwiększa się wiarygodność wewnętrzna, ale często kosztem wiarygodności zewnętrznej, ponieważ wprowadza się sztuczne warunki, które nie istnieją w rzeczywistości. W przeciwieństwie do tego, badania korelacyjne mają zazwyczaj niską wiarygodność wewnętrzną, ponieważ nic nie jest manipulowane lub kontrolowane, ale często mają wysoką wiarygodność zewnętrzną. Ponieważ eksperymentator niczym nie manipuluje ani niczego nie kontroluje, jest bardziej prawdopodobne, że wyniki odzwierciedlają związki istniejące w świecie rzeczywistym.

Wreszcie, rozszerzając ten kompromis między wewnętrzną i zewnętrzną ważnością, badania korelacyjne mogą pomóc w dostarczeniu zbieżnych dowodów dla teorii. Jeśli teoria jest poparta prawdziwym eksperymentem, który ma wysoką wiarygodność wewnętrzną, a także badaniami korelacyjnymi, które mają wysoką wiarygodność zewnętrzną, wówczas badacze mogą mieć większą pewność co do słuszności swojej teorii. Jako konkretny przykład, badania korelacyjne wykazujące, że istnieje związek między oglądaniem brutalnej telewizji a agresywnym zachowaniem zostały uzupełnione badaniami eksperymentalnymi potwierdzającymi, że związek ten ma charakter przyczynowy (Bushman & Huesmann, 2001).

Czy badania korelacyjne zawsze obejmują zmienne ilościowe?

Powszechnym błędnym przekonaniem wśród początkujących badaczy jest to, że badania korelacyjne muszą obejmować dwie zmienne ilościowe, takie jak wyniki w dwóch testach ekstrawersji lub liczba codziennych kłopotów i liczba objawów, których ludzie doświadczyli. Jednakże cechą definiującą badania korelacyjne jest to, że dwie zmienne są mierzone – żadna z nich nie jest manipulowana – i jest to prawdą niezależnie od tego, czy zmienne są ilościowe czy kategoryczne. Wyobraźmy sobie na przykład, że badacz podaje Skalę Samooceny Rosenberga 50 amerykańskim studentom college’u i 50 japońskim. Chociaż „wydaje się”, że jest to eksperyment międzyprzedmiotowy, jest to badanie korelacyjne, ponieważ badacz nie manipulował narodowościami studentów. Podobnie jest w przypadku badania Cacioppo i Petty’ego, w którym porównano wykładowców college’u i pracowników fabryki pod względem ich potrzeby poznawczej. Jest to badanie korelacyjne, ponieważ badacze nie manipulowali zawodami uczestników.

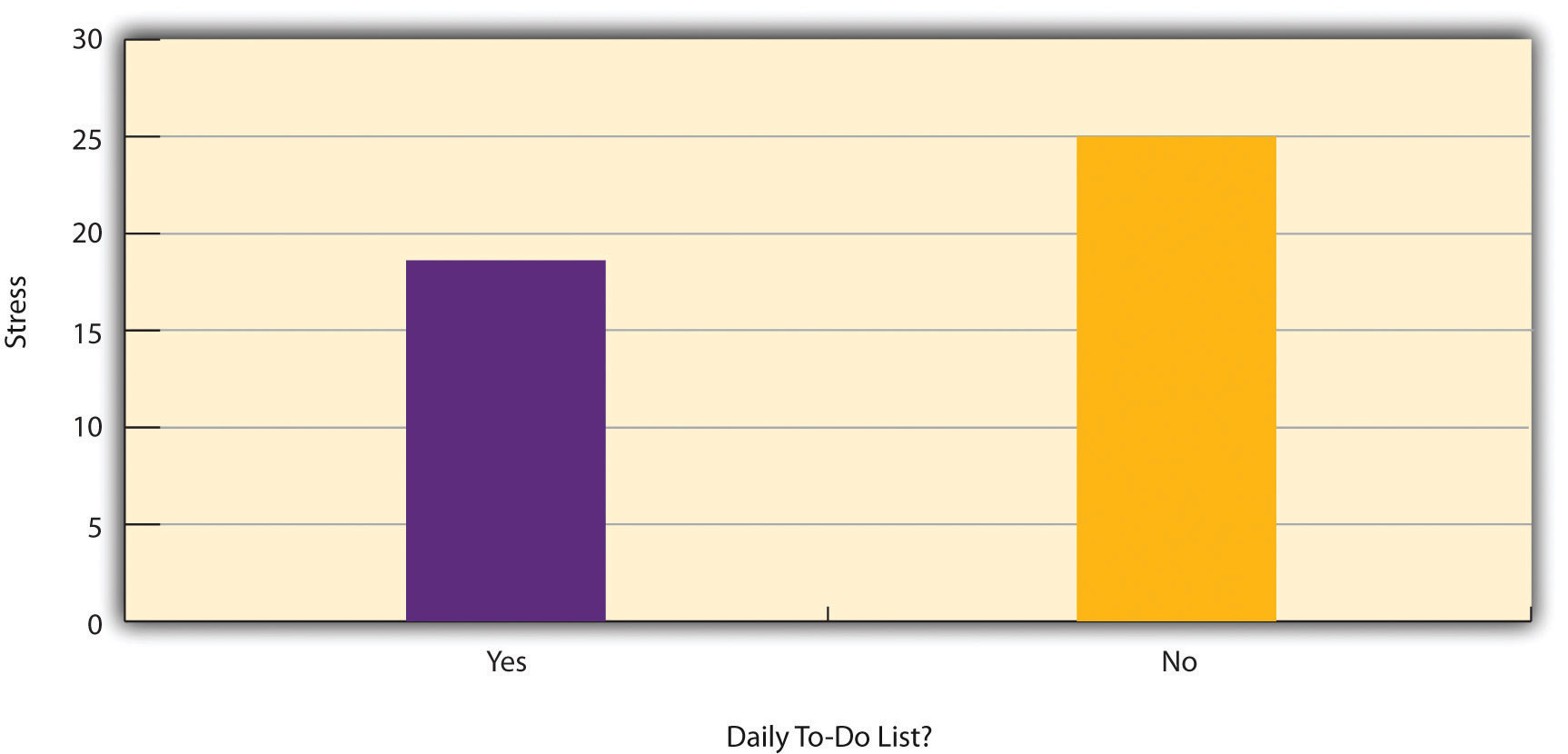
Rysunek 6.2 przedstawia dane z hipotetycznego badania nad związkiem między tym, czy ludzie robią codziennie listę rzeczy do zrobienia („listę rzeczy do zrobienia”), a stresem. Zauważ, że nie jest jasne, czy jest to eksperyment czy badanie korelacyjne, ponieważ nie jest jasne, czy zmienna niezależna była manipulowana. Jeśli badacz losowo przypisał niektórych uczestników do robienia codziennych list rzeczy do zrobienia, a innych nie, to jest to eksperyment. Jeśli badacz po prostu zapytał uczestników, czy robią codzienne listy rzeczy do zrobienia, to jest to badanie korelacyjne. To rozróżnienie jest ważne, ponieważ gdyby badanie było eksperymentem, można by wyciągnąć wniosek, że robienie codziennych list rzeczy do zrobienia zmniejszyło stres uczestników. Gdyby jednak było to badanie korelacyjne, można by jedynie stwierdzić, że zmienne te są statystycznie powiązane. Być może bycie zestresowanym ma negatywny wpływ na zdolność ludzi do planowania z wyprzedzeniem (problem kierunkowości). A może ludzie, którzy są bardziej sumienni, częściej robią listy rzeczy do zrobienia i rzadziej są zestresowani (problem trzeciej zmiennej). Kluczową kwestią jest to, że tym, co definiuje badanie jako eksperymentalne lub korelacyjne, nie są badane zmienne, ani to, czy zmienne są ilościowe czy kategoryczne, ani rodzaj wykresu czy statystyki użytej do analizy danych. To, co definiuje badanie, to sposób jego przeprowadzenia.

Data Collection in Correlational Research

Again, the defining feature of correlational research is that neither variable is manipulated. Nie ma znaczenia, jak lub gdzie zmienne są mierzone. Badacz może poprosić uczestników, aby przyszli do laboratorium i wypełnili skomputeryzowane zadanie polegające na podawaniu cyfr do tyłu oraz skomputeryzowane zadanie polegające na podejmowaniu ryzykownych decyzji, a następnie ocenić związek między wynikami uczestników w tych dwóch zadaniach. Albo badacz może udać się do centrum handlowego i zapytać ludzi o ich stosunek do środowiska i ich zwyczaje zakupowe, a następnie ocenić związek między tymi dwiema zmiennymi. Oba te badania byłyby korelacyjne, ponieważ żadna niezależna zmienna nie jest manipulowana.

Korelacje między zmiennymi ilościowymi

Korelacje między zmiennymi ilościowymi są często przedstawiane za pomocą wykresów rozrzutu. Rysunek 6.3 przedstawia pewne hipotetyczne dane dotyczące związku między ilością stresu, jaki odczuwają ludzie, a liczbą występujących u nich objawów fizycznych. Każdy punkt na wykresie rozrzutu reprezentuje wynik jednej osoby w obu zmiennych. Na przykład, zakreślony punkt na rysunku 6.3 reprezentuje osobę, której wynik w zakresie stresu wyniósł 10 i która miała trzy objawy fizyczne. Biorąc pod uwagę wszystkie punkty, można zauważyć, że osoby bardziej zestresowane zwykle mają więcej objawów fizycznych. Jest to dobry przykład pozytywnego związku, w którym wyższe wyniki jednej zmiennej mają tendencję do wiązania się z wyższymi wynikami drugiej zmiennej. Innymi słowy, poruszają się one w tym samym kierunku, albo obie w górę, albo obie w dół. Negatywna relacja to taka, w której wyższe wyniki jednej zmiennej mają tendencję do bycia kojarzonymi z niższymi wynikami drugiej zmiennej. Innymi słowy, poruszają się one w przeciwnych kierunkach. Na przykład istnieje ujemny związek między stresem a funkcjonowaniem układu odpornościowego, ponieważ wyższy stres wiąże się z niższym funkcjonowaniem układu odpornościowego.

Siła korelacji między zmiennymi ilościowymi jest zwykle mierzona za pomocą statystyki zwanej współczynnikiem korelacji Pearsona (lub r Pearsona). Jak pokazano na rysunku 6.4, współczynnik Pearsona przyjmuje wartości od -1,00 (najsilniejsza możliwa zależność ujemna) do +1,00 (najsilniejsza możliwa zależność dodatnia). Wartość 0 oznacza, że nie ma związku między dwiema zmiennymi. Kiedy r Pearsona wynosi 0, punkty na wykresie rozrzutu tworzą bezkształtną „chmurę”. W miarę jak jego wartość przesuwa się w kierunku -1,00 lub +1,00, punkty coraz bardziej zbliżają się do jednej linii prostej. Współczynniki korelacji bliskie ±.10 uważane są za małe, wartości bliskie ±.30 za średnie, a wartości bliskie ±.50 za duże. Zauważ, że znak współczynnika r Pearsona nie jest związany z jego siłą. Na przykład wartości r Pearsona +,30 i -,30 są równie silne; chodzi tylko o to, że jedna z nich reprezentuje umiarkowanie pozytywny związek, a druga umiarkowanie negatywny związek. Z wyjątkiem współczynników wiarygodności, większość korelacji, które znajdujemy w psychologii, jest niewielka lub umiarkowana pod względem wielkości. Strona internetowa http://rpsychologist.com/d3/correlation/, stworzona przez Kristoffera Magnussona, zapewnia doskonałą interaktywną wizualizację korelacji, która pozwala na dostosowanie siły i kierunku korelacji przy jednoczesnym obserwowaniu odpowiednich zmian na wykresie rozrzutu.

Istnieją dwie powszechne sytuacje, w których wartość współczynnika r Pearsona może być myląca. Pearson’s r jest dobrą miarą tylko dla liniowych relacji, w których punkty są najlepiej przybliżone przez linię prostą. Nie jest to dobra miara dla zależności nieliniowych, w których punkty są lepiej przybliżone przez linię zakrzywioną. Rysunek 6.5 przedstawia na przykład hipotetyczną zależność między ilością snu, jaką ludzie otrzymują w ciągu nocy, a ich poziomem depresji. W tym przykładzie linia, która najlepiej przybliża punkty, jest krzywą – czymś w rodzaju odwróconej litery „U” – ponieważ ludzie, którzy śpią około ośmiu godzin, są zazwyczaj najmniej przygnębieni. Ci, którzy śpią za mało i ci, którzy śpią za dużo, mają tendencję do większej depresji. Mimo że na rysunku 6.5 widać dość silny związek między depresją a snem, współczynnik r Pearsona byłby bliski zeru, ponieważ punktów na wykresie rozrzutu nie da się dobrze dopasować do jednej linii prostej. Oznacza to, że przed użyciem współczynnika r Pearsona ważne jest wykonanie wykresu rozrzutu i potwierdzenie, że związek jest w przybliżeniu liniowy. Nieliniowe związki są dość powszechne w psychologii, ale mierzenie ich siły wykracza poza zakres tej książki.

Inną częstą sytuacją, w której wartość r Pearsona może być myląca, jest sytuacja, w której jedna lub obie zmienne mają ograniczony zakres w próbie w stosunku do populacji. Ten problem jest określany jako ograniczenie zakresu. Załóżmy na przykład, że istnieje silna ujemna korelacja między wiekiem ludzi a ich upodobaniem do muzyki hip-hopowej, jak pokazano na wykresie rozrzutu na rysunku 6.6. Współczynnik r Pearsona wynosi tutaj -,77. Gdybyśmy jednak mieli zbierać dane tylko od osób w wieku od 18 do 24 lat – reprezentowanych przez zacieniony obszar na rysunku 6.6 – wówczas związek ten wydawałby się dość słaby. W rzeczywistości współczynnik r Pearsona dla tego ograniczonego zakresu wieku wynosi 0. Dlatego dobrym pomysłem jest projektowanie badań w taki sposób, aby uniknąć ograniczania zakresu. Na przykład, jeśli wiek jest jedną z głównych zmiennych, można zaplanować zbieranie danych od osób w szerokim przedziale wiekowym. Ponieważ jednak ograniczenie zakresu nie zawsze jest przewidywalne lub łatwe do uniknięcia, dobrą praktyką jest sprawdzenie danych pod kątem możliwego ograniczenia zakresu i zinterpretowanie r Pearsona w świetle tego ograniczenia. (Istnieją również statystyczne metody korygowania współczynnika r Pearsona ze względu na ograniczenie zakresu, ale wykraczają one poza zakres tej książki).

Korelacja nie implikuje związku przyczynowego

Prawdopodobnie wielokrotnie słyszałeś, że „korelacja nie implikuje związku przyczynowego”. Zabawny przykład tego pochodzi z badania z 2012 roku, które wykazało pozytywną korelację (Pearson’s r = 0,79) między konsumpcją czekolady na osobę w danym kraju a liczbą nagród Nobla przyznanych obywatelom tego kraju. Wydaje się jednak jasne, że nie oznacza to, że jedzenie czekolady powoduje, że ludzie zdobywają nagrody Nobla, i nie miałoby sensu próbować zwiększyć liczbę zdobytych nagród Nobla poprzez zalecanie rodzicom, aby karmili swoje dzieci większą ilością czekolady.

Istnieją dwa powody, dla których korelacja nie oznacza związku przyczynowego. Pierwszy z nich nazywa się problemem kierunkowości. Dwie zmienne, X i Y, mogą być statystycznie powiązane, ponieważ X powoduje Y lub ponieważ Y powoduje X. Rozważmy, na przykład, badanie pokazujące, że to, czy ludzie ćwiczą, czy nie, jest statystycznie związane z tym, jak szczęśliwi są – tak, że ludzie, którzy ćwiczą, są średnio szczęśliwsi niż ludzie, którzy nie ćwiczą. Ten statystyczny związek jest spójny z ideą, że ćwiczenia powodują szczęście, ale jest również spójny z ideą, że szczęście powoduje ćwiczenia. Być może bycie szczęśliwym daje ludziom więcej energii lub skłania ich do szukania okazji do socjalizacji z innymi poprzez chodzenie na siłownię. Drugi powód, dla którego korelacja nie implikuje związku przyczynowego, nazywany jest problemem trzeciej zmiennej. Dwie zmienne, X i Y, mogą być statystycznie powiązane nie dlatego, że X powoduje Y, lub że Y powoduje X, ale dlatego, że jakaś trzecia zmienna, Z, powoduje zarówno X, jak i Y. Na przykład fakt, że narody, które zdobyły więcej nagród Nobla, mają tendencję do wyższej konsumpcji czekolady, prawdopodobnie odzwierciedla geografię, ponieważ kraje europejskie mają tendencję do wyższych wskaźników konsumpcji czekolady per capita i inwestują więcej w edukację i technologię (ponownie, per capita) niż wiele innych krajów na świecie. Podobnie, statystyczny związek między ćwiczeniami a szczęściem może oznaczać, że jakaś trzecia zmienna, taka jak zdrowie fizyczne, powoduje obie te cechy. Bycie zdrowym fizycznie może powodować, że ludzie ćwiczą i dzięki temu są szczęśliwsi. Korelacje, które są wynikiem trzeciej zmiennej są często określane jako korelacje pozorne.

Kilka doskonałych i zabawnych przykładów pozornych korelacji można znaleźć na stronie http://www.tylervigen.com (Rysunek 6.7 przedstawia jeden z takich przykładów).

.