Obwód okręgu – Objaśnienia i przykłady

Widzieliśmy wcześniej jak znaleźć obwód wielokąta. Wiemy, że okrąg nie jest wielokątem, dlatego nie powinien mieć obwodu. Używamy równoważnej formy dla okręgu, zwanej obwodem.

W tym artykule omówimy, jak znaleźć obwód okręgu, wzór na obwód okręgu i przykładowe zadania dotyczące obwodu okręgu.

Co to jest obwód okręgu?

Dystans wokół wielokąta, takiego jak kwadrat lub prostokąt, nazywamy obwodem (P). Z drugiej strony, odległość wokół okręgu jest nazywana obwodem (C). Dlatego obwód okręgu jest liniową odległością krawędzi okręgu.

Dlaczego musimy obliczać obwód okręgu?

Znalezienie obwodu obiektu jest ważne w następujących sytuacjach:

Czy chcesz kupić biustonosz, spodnie lub sweter, musisz znać odległość wokół talii lub klatki piersiowej. Chociaż Twoje ciało nie jest idealnym okręgiem, musisz zmierzyć jego obwód za pomocą taśmy mierniczej. Krawcy najczęściej używają tej techniki do określenia obwodu sukienki.

Trzeba również znać obwód koła, wykonując prace rzemieślnicze, stawiając ogrodzenie wokół jacuzzi lub po prostu rozwiązując zadanie matematyczne w szkole.

Jak znaleźć obwód koła?

Jak wspomniano wcześniej, obwód lub obwód koła to odległość wokół koła lub dowolnego okrągłego kształtu. Obwód okręgu jest taki sam jak długość linii prostej, która jest zaginana lub załamywana, aby utworzyć okrąg. Obwód okręgu mierzy się w metrach, kilometrach, jardach, calach itp.

Istnieją dwa sposoby znajdowania obwodu lub obwodu okręgu. Pierwsza formuła polega na użyciu promienia, a druga na użyciu średnicy okręgu. Ważne jest, aby zauważyć, że obie te metody dają ten sam wynik.

Przyjrzyjmy się temu.

Obwód okręgu jest dany przez;

C = 2 * π* R = 2πR

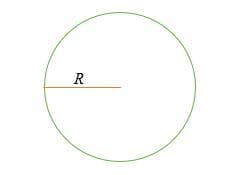
gdzie,

C = obwód lub obwód,

R = promień okręgu,

π = stała matematyczna znana jako Pi

Or

C = π* D = π D

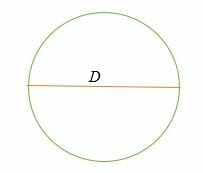
gdzie, D = 2R = średnica okręgu

Dla dowolnego okręgu stosunek jego obwodu do średnicy jest równy stałej znanej jako pi.

Obwód/średnica = Pi

C /D = Pi lub C/2R = pi

Przybliżona wartość pi (π) = 22/7 = 3.1415926535897…. (wartość niekończąca)

Dla łatwiejszego obliczania obwodu okręgu przyjmuje się, że wartość pi wynosi 3,14 (π = 3,14).

Zobaczmy poniżej kilka przykładów, aby doszlifować pojęcie obwodu.

Przykład 1

Znajdź obwód okręgu o promieniu 8 cm.

Rozwiązanie

Obwód = 2 * π* R = 2πR

= 2 * 3,14 * 8

= 50,24 cm.

Przykład 2

Oblicz obwód okręgu, którego średnica wynosi 70 mm

Rozwiązanie

Obwód = π* D = π D

= 3,14 * 70

= 219.8 mm

Przykład 3

Oblicz obwód okrągłego ogrodu kwiatowego, którego promień wynosi 10 m.

Rozwiązanie

Obwód = 2 * π* R = 2πR

= 2 * 3,14 * 10

= 62,8 m.

Przykład 4

Obwód pewnego koła wynosi 440 jardów. Znajdź średnicę i promień tego okręgu.

Rozwiązanie

Obwód = 2 * π* R = 2πR

440 =2 * 3,14 * R

440 = 6.28R

Podziel obie strony przez 6,28, aby otrzymać,

R = 70,06

Więc promień okręgu wynosi 70,06 jardów. Ale skoro średnica jest dwa razy większa od promienia okręgu, to średnica jest równa 140,12 jardów.

Przykład 5

Średnica kół roweru wynosi 100 cm. Ile obrotów wykona każde koło, aby przejechać odległość 157 metrów

Rozwiązanie

Oblicz obwód koła roweru.

Obwód = π D

= 3.14 * 100

= 314 cm

Aby otrzymać liczbę obrotów koła, podziel pokonaną odległość przez obwód koła.

Przed podzieleniem musimy zamienić 157 metrów na cm, więc mnożymy 157 przez 100, aby otrzymać 15700 cm. Wobec tego,

Liczba obrotów = 15700 cm/314 cm

= 50 obrotów.

Przykład 6

Przedziałek drutu w postaci prostokąta o długości 100 cm i szerokości 50 cm rozcięto i złożono tak, aby powstało koło. Oblicz obwód i promień powstałego okręgu.

Rozwiązanie

Obwód powstałego okręgu = obwód prostokątnego drutu.

Obwód prostokąta = 2(L + W)

= 2(100 + 50) cm

= 2 * 150 cm

= 300 cm.

Więc obwód okręgu będzie wynosił 300 cm.

Teraz oblicz jego promień.

Obwód = 2 π R

300 cm = 2 * π * R

300 cm = 2 * 3,14 * R

300 cm = 6,28R

Podziel obie strony przez 6,28.

R = 47.77 cm

Promień okręgu będzie więc wynosił 47,77 cm.

Przykład 7

Promień każdego z kół motocykla wynosi 0. 85 m. Jak daleko będzie się poruszał motocykl, jeśli każde z kół wykona 1000 obrotów. Przyjmij, że motocykl porusza się po linii prostej.

Rozwiązanie

Najpierw znajdź obwód koła.

Obwód = 2 π R

= 2 * 3,14 * 0,85

= 5,338 m.

Aby znaleźć przebytą drogę, pomnóż obwód koła przez liczbę wykonanych obrotów.

Odległość = 5,338 * 1000

= 5338 m

Więc przebyta odległość jest równa 5,338 km.

Praktyczne pytania

1. Dla Mike’a i jego przyjaciół podano 12-calową pizzę. Mike jest zainteresowany obliczeniem jej obwodu. Pomóż mu!
2. Obwód pewnego kwadratu jest równy 1/3 pola pewnego koła. Jeśli długość kwadratu wynosi L jednostek, wyznacz średnicę okręgu w zakresie L.

Odpowiedzi

1. 12π cali lub 37.67 cali
2. 12L/π jednostek

Previous Lesson | Main Page | Next Lesson

.