Funkcje lub odwzorowania

Teraz, w funkcjach lub odwzorowaniach będziemy uczyć się o specjalnym rodzaju relacji zwanych funkcjami lub odwzorowaniami. Aby je zrozumieć, weźmy kilka prawdziwych przykładów z życia.

Wszystkie te pytania mają
jednakowe odpowiedzi. Zobaczmy
jak możemy to odnieść
do mapowania uczenia się.

● Skąd wschodzi słońce?

Wschód

● Jaka jest stolica Indii?

Delhi

● Jaki jest następca liczby 4?

5

● Jaka jest suma liczb 5 i 3?

8

Odwzorowanie lub funkcje:

Jeżeli A i B są dwoma niepustymi zbiorami, to relację 'f’ ze zbioru A do zbioru B nazywamy funkcją lub odwzorowaniem,
● Jeżeli z każdym elementem zbioru A związany jest unikalny element zbioru B.

● Funkcję 'f’ z A do B oznaczamy przez f : A → B.

● Jeśli f jest funkcją z A do B i x ∈ A, to f(x) ∈ B, gdzie f(x) nazywamy obrazem x pod f, a x nazywamy przedobrazem f(x) pod 'f’.

Uwaga:

Aby f było odwzorowaniem z A na B:

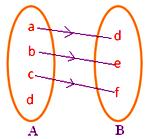
● Każdy element A musi mieć obraz w B. Rysunek obok nie reprezentuje odwzorowania, ponieważ element d w zbiorze A nie jest związany z żadnym elementem zbioru B.

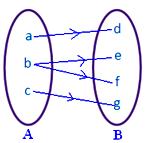
● Żaden element A nie może mieć więcej niż jednego obrazu. Rysunek obok nie przedstawia odwzorowania, ponieważ element b ze zbioru A jest związany z dwoma elementami d, f ze zbioru B.

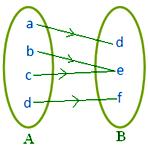
● Różne elementy A mogą mieć ten sam obraz w B. Przylegająca figura reprezentuje odwzorowanie.

Uwaga:

Każde odwzorowanie jest relacją, ale każda relacja może nie być odwzorowaniem.

Funkcja jako szczególny rodzaj relacji:

Przypomnijmy i przejrzyjmy funkcję jako szczególny rodzaj relacji Załóżmy, że A i B są dwoma niepustymi zbiorami, wtedy reguła 'f’, która kojarzy każdy element A z unikalnym elementem B nazywana jest funkcją lub odwzorowaniem z A na B.
Jeśli 'f’ jest odwzorowaniem z A na B,

wyrażamy to jako f: A → B

czytamy to jako 'f’ jest funkcją z A na B.
Jeśli 'f ’ jest funkcją z A na B i x∈A i y∈B, to mówimy, że y jest obrazem elementu x pod funkcją ’ f ’ i oznaczamy go przez f(x).
Zapisujemy to jako y = f(x)

Tutaj element x nazywamy przedobrazem y.

Tak więc dla funkcji z A do B.
● A i B powinny być niepuste.

● Każdy element A powinien mieć obraz w B.

● Żaden element 'A’ nie powinien mieć więcej niż jeden obraz w 'B’.
Uwaga:

● Dwa lub więcej elementów A może mieć ten sam obraz w B.

● f : x → y oznacza, że pod funkcją 'f’ z A do B, element x z A ma obraz y w B.

● Konieczne jest, aby każdy obraz f był w B, ale mogą istnieć pewne elementy w B, które nie są obrazami f żadnego elementu A.

● Relacje i odwzorowania

Para uporządkowana

Iloczyn kartezjański dwóch zbiorów

Relacja

Domena i zakres relacji

Funkcje lub odwzorowania

Domena Co-Dziedzina i zakres funkcji

● Relacje i odwzorowania – Arkusze

7-klasowe zadania matematyczne

8-klasowe ćwiczenia matematyczne
Od funkcji lub odwzorowania do STRONY GŁÓWNEJ

.