Dlaczego 0.999… równa się 1?!

Innym sposobem myślenia o terminach w naszym sumowaniu jest to, że każdy kolejny termin jest otrzymywany przez pomnożenie poprzedniego terminu przez wspólny stosunek.

To oznacza, że mamy szereg geometryczny, który zbiega do a/(1 – r), gdzie a jest pierwszą wartością w szeregu, a r jest stosunkiem, przez który mnożymy, aby otrzymać następny termin.

Konwergencja w szeregu oznacza po prostu, że szereg będzie coraz bardziej zbliżał się do określonej wartości, gdy będziemy dodawać do niego coraz więcej terminów. Seria jest coraz nieskończenie blisko wartości zbieżności. W nieskończonej skali zbieżność staje się równością.

W naszym przypadku zaczynamy od 1/10 i za każdym razem mnożymy przez 1/10, więc zarówno a, jak i r = 1/10.

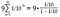
Dokończ arytmetykę po prawej stronie.

Teraz formalnie pokazaliśmy, że 0.999… zbiega się do lub jest równe 1.

Pomysły końcowe &Inspiracja

Jeśli wydaje Ci się to dziwne, to dobrze! Wiesz, że dwie różne liczby, powinny w rzeczywistości być różnymi liczbami. Kontrintuicyjna natura tego problemu jest nieodłączna od dziwności, która towarzyszy pracy z nieskończonością.

Nawet w prostym problemie, takim jak ten, przechodzisz z granic tego, co jest namacalne dla ludzkiego mózgu na skalę, która jest w pewien sposób poza naszym zrozumieniem. Jako istoty skończone możemy chwytać się zrozumienia koncepcji nieskończoności lub wieczności, ale nigdy nie możemy jej prawdziwie doświadczyć. Co oznacza, że często to, co wiemy, że jest prawdziwe w naszym skończonym świecie, okazuje się zachowywać inaczej na nieskończonym poziomie.

Zaakceptowanie przejścia od łatwo odkrywalnej i odtwarzalnej matematyki do tego, co może być tylko przetestowane i wyobrażone w naszych umysłach jest częścią piękna i cudu matematyki.

Więc nie bierz dzisiejszej lekcji za wartość nominalną i wzruszaj ramionami.

Pozwól, aby między tobą a doskonałym zrozumieniem była warstwa mgły. Niech twój umysł zostanie zdmuchnięty przez fakt, że nieskończoność zachowuje się dziwnie. I niech to sprawi, że zapragniesz więcej zrozumienia, a przede wszystkim więcej matematyki.

Dziękuję za czytanie i rozważanie nieskończoności razem ze mną dzisiaj!