2.12: Równanie Van der Waalsa

Równanie van der Waalsa rozszerza równanie gazu idealnego w prosty sposób. Równanie Van der Waalsa ma postać

Pasuje ono do danych ciśnienie-wolumen-temperatura dla gazu rzeczywistego lepiej niż równanie gazu idealnego. Lepsze dopasowanie uzyskuje się poprzez wprowadzenie dwóch parametrów (oznaczonych „a” i „b”), które muszą być wyznaczone doświadczalnie dla każdego gazu. Równanie Van der Waalsa jest szczególnie przydatne w naszych wysiłkach, aby zrozumieć zachowanie rzeczywistych gazów, ponieważ ucieleśnia prosty fizyczny obraz różnicy pomiędzy gazem rzeczywistym a gazem idealnym.

W wyprowadzeniu prawa Boyle’a z praw Newtona zakładamy, że cząsteczki gazu nie oddziałują ze sobą. Proste argumenty pokazują, że może to być prawda tylko w przybliżeniu. Rzeczywiste cząsteczki gazu muszą oddziaływać na siebie nawzajem. Na małych odległościach odpychają się wzajemnie. Na nieco większych odległościach przyciągają się wzajemnie. Równanie gazu idealnego może być również wyprowadzone z podstawowych założeń, które przyjęliśmy w §10, poprzez zastosowanie teorii termodynamiki statystycznej. Przyjmując różne założenia dotyczące własności cząsteczek, możemy zastosować termodynamikę statystyczną do wyprowadzenia równania van der Waalsa. Wymagane założenia są takie, że cząsteczki zajmują skończoną objętość i że przyciągają się wzajemnie z siłą, która zmienia się jako odwrotność potęgi odległości między nimi. (Zazwyczaj przyjmuje się, że siła przyciągania jest proporcjonalna do ^{-6}}.)

Aby zrozumieć, że rzeczywiste cząsteczki gazu zarówno przyciągają się, jak i odpychają, wystarczy pamiętać, że każdy gaz można skroplić, obniżając jego temperaturę i zwiększając przyłożone do niego ciśnienie. Jeśli jeszcze bardziej schłodzimy ciecz, zamieni się ona w ciało stałe. Dwie cechy wyróżniające ciało stałe to fakt, że zachowuje ono swój kształt i jest prawie nieściśliwe. Nieściśliwość ciała stałego przypisujemy siłom odpychającym pomiędzy jego cząsteczkami; zbliżyły się one do siebie tak bardzo, że siły odpychające pomiędzy nimi stały się ważne. Aby skompresować ciało stałe, molekuły muszą być jeszcze bardziej zbliżone do siebie, co wymaga użycia nadmiernej siły. Z drugiej strony, jeśli rzucimy kostką lodu przez pokój, wszystkie cząsteczki wody, które się na nią składają, lecą przez pokój razem. Najwyraźniej cząsteczki wody w ciele stałym są do siebie przyciągane, w przeciwnym razie rozeszłyby się każdy w swoją stronę – rzucenie kostką lodu byłoby jak rzucenie garścią suchego piasku. Ale cząsteczki wody są te same cząsteczki niezależnie od temperatury lub ciśnienia, więc jeśli istnieją siły przyciągania i odpychania między nimi w ciele stałym, siły te muszą być obecne w fazie ciekłej i gazowej również.

W fazie gazowej, cząsteczki są daleko od siebie; w cieczy lub fazy stałej, są one pakowane razem. W temperaturze wrzenia, objętość cieczy jest znacznie mniejsza niż objętość gazu, z którego jest skondensowany. W punkcie zamarzania objętość ciała stałego tylko nieznacznie różni się od objętości cieczy, z której jest zamrożone, a na pewno jest większa od zera. Te powszechne obserwacje można łatwo wytłumaczyć, zakładając, że każda cząsteczka ma charakterystyczną objętość. Możemy to z kolei rozumieć jako konsekwencję natury sił międzycząsteczkowych; najwyraźniej siły te stają się coraz silniejsze, gdy zmniejsza się odległość między parą cząsteczek. Ponieważ ciecz lub ciało stałe zajmuje określoną objętość, siła odpychająca musi rosnąć szybciej niż siła przyciągająca, gdy odległość międzycząsteczkowa jest mała. Często użyteczne jest mówienie o objętości molowej fazy skondensowanej. Przez objętość molową rozumiemy objętość jednego mola czystej substancji. Objętość molowa fazy skondensowanej jest określona przez odległość międzycząsteczkową, przy której występuje równowaga między międzycząsteczkowymi siłami przyciągania i odpychania.

W fazach skondensowanych cząsteczki są oczywiście bardzo blisko siebie. Jeśli przyjmiemy, że puste przestrzenie między cząsteczkami są pomijalne, objętość fazy skondensowanej jest w przybliżeniu równa liczbie cząsteczek w próbce pomnożonej przez objętość pojedynczej cząsteczki. Wówczas objętość molowa jest liczbą Avogadro’a pomnożoną przez objętość zajmowaną przez jedną cząsteczkę. Jeśli znamy gęstość, D, i masę molową, \(\overline{M}), możemy znaleźć objętość molową, \(\overline{V}), jako

Objętość zajmowana przez cząsteczkę, V, przyjmuje postać

Ciśnienie i objętość występujące w równaniu van der Waalsa są ciśnieniem i objętością rzeczywistego gazu. Możemy odnieść pojęcia z równania van der Waalsa do równania gazu idealnego: Dobrze jest myśleć o pojęciach \(\lewa(P+{{an}^2}/{V^2}}prawa)\) i \(\lewa(V-nb-prawa)\) jako o ciśnieniu i objętości hipotetycznego gazu idealnego. Czyli

&=nRT ¨end{align*}]

Następnie mamy

Równanie gazu idealnego wyprowadzamy z modelu, w którym cząsteczki są nie oddziałującymi ze sobą masami punktowymi. Zatem objętość gazu idealnego to objętość zajmowana przez gaz, którego poszczególne cząsteczki mają zerową objętość. Jeśli poszczególne cząsteczki gazu rzeczywistego efektywnie zajmują objętość \(b}/{overline{N}}), to ich \(n\) mole efektywnie zajmują objętość

Równanie Van der Waalsa mówi, że objętość gazu rzeczywistego to objętość, którą zajmowałyby nie oddziałujące ze sobą masy punktowe, \(V_{idealny gaz}}), plus efektywna objętość samych cząsteczek gazu. (Gdy dane dla rzeczywistych cząsteczek gazu są dopasowywane do równania van der Waalsa, wartość Δ(b) jest zwykle nieco większa niż objętość oszacowana na podstawie gęstości cieczy i masy cząsteczkowej. Patrz problem 24.)

Podobnie mamy

Możemy to rozumieć jako logiczną konsekwencję przyciągających oddziaływań między cząsteczkami rzeczywistego gazu. Z tego wynika, że ciśnienie gazu rzeczywistego jest mniejsze od ciśnienia hipotetycznego gazu idealnego o wartość proporcjonalną do ^2. Stała proporcjonalności wynosi ^2. Ponieważ ∗ jest gęstością molową (molami na jednostkę objętości) cząsteczek gazu, jest to miara stężenia. Liczba zderzeń pomiędzy cząsteczkami tego samego rodzaju jest proporcjonalna do kwadratu ich koncentracji. (Rozważymy ten punkt bardziej szczegółowo w rozdziałach 4 i 5.) Zatem ^2 jest miarą częstotliwości, z jaką rzeczywiste cząsteczki gazu wchodzą ze sobą w bliski kontakt. Jeśli przyciągają się one wzajemnie, gdy się do siebie zbliżają, efekt tego przyciągania powinien być proporcjonalny do ^2). Tak więc równanie van der Waalsa jest zgodne z ideą, że ciśnienie rzeczywistego gazu różni się od ciśnienia hipotetycznego gazu idealnego o wielkość, która jest proporcjonalna do częstotliwości i siły przyciągających oddziaływań.

Ale dlaczego przyciągające oddziaływania powinny mieć taki efekt; dlaczego ciśnienie rzeczywistego gazu powinno być mniejsze niż ciśnienie hipotetycznego gazu idealnego? Być może najlepszym sposobem na stworzenie jakościowego obrazu jest uznanie, że przyciągające siły międzycząsteczkowe mają tendencję do powodowania zbijania się cząsteczek gazu. W końcu to właśnie te przyciągające siły powodują, że w niskich temperaturach cząsteczki łączą się w ciecz. Powyżej temperatury wrzenia zdolność cząsteczek gazu do rozchodzenia się w różne strony ogranicza skutki tej tendencji; jednak nawet w gazie siły przyciągające muszą działać w sposób, który ma tendencję do zmniejszania objętości zajmowanej przez cząsteczki. Ponieważ objętość zajmowana przez gaz jest podyktowana wielkością pojemnika, a nie właściwościami samego gazu, ta tendencja do zbijania się w grudki znajduje wyraz w spadku ciśnienia.

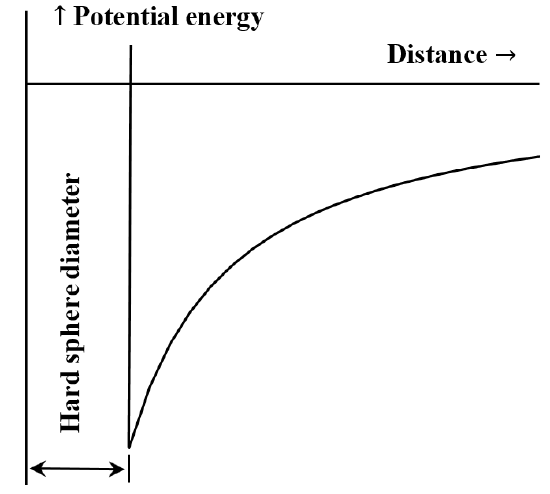
Często użyteczne jest opisanie oddziaływania pomiędzy cząsteczkami lub cząsteczkami chemicznymi w kategoriach wykresu energii potencjalnej w funkcji odległości. Równanie van der Waalsa odpowiada przypadkowi, w którym odpychające oddziaływanie między cząsteczkami nie istnieje, dopóki cząsteczki się nie zetkną. Gdy już się zetkną, energia potrzebna do ich dalszego zbliżenia staje się arbitralnie duża. Często opisuje się to mówiąc, że zachowują się one jak „twarde kule”. Siła przyciągania między dwoma cząsteczkami maleje wraz ze wzrostem odległości między nimi. Gdy są one od siebie bardzo oddalone, oddziaływanie przyciągające jest bardzo małe. Mówimy, że energia oddziaływania jest równa zeru, gdy cząsteczki są nieskończenie daleko od siebie. Jeśli na początku mamy dwie szeroko oddalone od siebie, nieruchome, wzajemnie przyciągające się cząsteczki, to będą one spontanicznie poruszać się w swoją stronę, zyskując energię kinetyczną. Ich energia potencjalna maleje w miarę zbliżania się do siebie, osiągając najmniejszą wartość, gdy cząsteczki stykają się ze sobą. Tak więc równanie van der Waalsa implikuje wykres zależności energii potencjalnej od odległości naszkicowany na rysunku 5.

.