Wat als uw gegevens NIET Normaal zijn?

Inleiding

Het is Halloweenweek, en tussen de trucs en traktaties door gniffelen wij, data geeks, over deze schattige meme op de sociale media.

Dacht je dat dit een grapje is? Laat me u vertellen, dit is geen lachertje. Het is angstaanjagend, in de geest van Halloween!

Als we er niet van uit kunnen gaan dat de meeste van onze gegevens (van zakelijke, sociale, economische of wetenschappelijke oorsprong) op zijn minst ongeveer ‘Normaal’ zijn (d.w.z. dat ze worden gegenereerd door een Gaussisch proces of door een som van meerdere van dergelijke processen), dan zijn we gedoemd!

Hier volgt een uiterst beknopte lijst van dingen die niet geldig zullen zijn,

• Het hele concept van six-sigma
• De beroemde 68-95-99.7 regel
• Het ‘heilige’ concept van p=0.05 (komt van 2 sigma interval) in statistische analyse

Geen eng genoeg? Laten we er meer over praten…

De almachtige en alomtegenwoordige normale verdeling

Laten we dit gedeelte kort en bondig houden.

De normale (Gaussische) verdeling is de meest bekende kansverdeling. Hier zijn enkele links naar artikelen die de kracht en brede toepasbaarheid ervan beschrijven,

• Waarom datawetenschappers van Gaussisch houden

• Hoe domineer je het statistiekgedeelte van je datawetenschapsinterview
• Wat is er zo belangrijk aan de normale verdeling?

Omwille van zijn verschijning in verschillende domeinen en de Central Limit Theorem (CLT), neemt deze verdeling een centrale plaats in binnen data science en analytics.

Dus, wat is het probleem?

Dit is allemaal hunky-dory, wat is het probleem?

Het probleem is dat je vaak een verdeling vindt voor je specifieke dataset, die misschien niet voldoet aan de Normaliteit, dat wil zeggen de eigenschappen van een Normale verdeling. Maar vanwege de te grote afhankelijkheid van de aanname van Normaliteit, zijn de meeste business analytics frameworks op maat gemaakt voor het werken met normaal verdeelde datasets.

Het zit bijna ingebakken in ons onderbewustzijn.

Stel dat u wordt gevraagd om te controleren of een nieuwe partij gegevens van een of ander proces (engineering of business) zinvol is. Met ‘zinvol’ bedoelt u of de nieuwe gegevens binnen het verwachte bereik vallen.

Wat is deze ‘verwachting’? Hoe kwantificeer je het bereik?

Automatisch, als door een onderbewuste drang gestuurd, meten we het gemiddelde en de standaardafwijking van de steekproefgegevensverzameling en gaan we na of de nieuwe gegevens binnen een bepaald standaardafwijkingsbereik vallen.

Als we met een 95%-betrouwbaarheidsgrens moeten werken, dan zijn we al blij als de gegevens binnen 2 standaardafwijkingen vallen. Als we een striktere grens nodig hebben, controleren we 3 of 4 standaardafwijkingen. We berekenen Cpk, of we volgen de zes-sigma richtlijnen voor ppm (parts-per-million) kwaliteitsniveau.

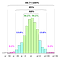
Al deze berekeningen zijn gebaseerd op de impliciete aanname dat de populatiegegevens (NIET de steekproef) een Gaussische verdeling volgen, d.w.z.D.w.z. dat het fundamentele proces waaruit alle gegevens zijn voortgekomen (in het verleden en op dit moment), wordt beheerst door het patroon aan de linkerkant.

Maar wat gebeurt er als de gegevens het patroon aan de rechterkant volgen?

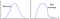
Of, dit, en… dat?

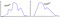
Is er een meer universele grens wanneer de gegevens NIET normaal zijn?

Op het einde van de dag hebben we nog steeds een wiskundig verantwoorde techniek nodig om onze betrouwbaarheidsgrens te kwantificeren, zelfs wanneer de gegevens niet normaal zijn. Dat betekent dat onze berekening een beetje kan veranderen, maar we moeten nog steeds zoiets kunnen zeggen als dit-

“De waarschijnlijkheid dat een nieuw gegevenspunt op een bepaalde afstand van het gemiddelde wordt waargenomen, is zodanig…”

Het is duidelijk dat we een meer universele grens moeten zoeken dan de gekoesterde Gaussische grenzen van 68-95-99.7 (overeenkomend met 1/2/3 standaarddeviaties afstand van het gemiddelde).

Er is gelukkig zo’n grens, de “Chebyshev-grens”.

Wat is de Chebyshev-grens en hoe is hij nuttig?

De ongelijkheid van Chebyshev (ook wel de ongelijkheid van Bienaymé-Chebyshev genoemd) garandeert dat voor een brede klasse van kansverdelingen niet meer dan een bepaalde fractie van de waarden meer dan een bepaalde afstand van het gemiddelde kan liggen.

In concreto: niet meer dan 1/k² van de waarden van de verdeling kan meer dan k standaardafwijkingen van het gemiddelde verwijderd zijn (of omgekeerd: ten minste 1-1/k² van de waarden van de verdeling ligt binnen k standaardafwijkingen van het gemiddelde).

Het is van toepassing op vrijwel onbeperkte soorten kansverdelingen en werkt met een veel soepeler aanname dan Normaliteit.

Hoe werkt het?

Zelfs als u niets weet over het geheime proces achter uw gegevens, is de kans groot dat u het volgende kunt zeggen,

“Ik ben ervan overtuigd dat 75% van alle gegevens binnen 2 standaarddeviaties van het gemiddelde moet vallen”,

Of,

Ik ben ervan overtuigd dat 89% van alle gegevens binnen 3 standaarddeviaties van het gemiddelde moet vallen”.

Hier ziet het eruit voor een willekeurig lijkende verdeling,

Hoe pas je het toe?

Zoals u inmiddels wel kunt raden, hoeft de basis van uw gegevensanalyse niet veel te veranderen. U verzamelt nog steeds een steekproef van de gegevens (hoe groter hoe beter), berekent dezelfde twee grootheden die u gewend bent te berekenen – gemiddelde en standaardafwijking, en past dan de nieuwe grenzen toe in plaats van de 68-95-99,7-regel.

De tabel ziet er als volgt uit (hier staat k voor zoveel standaardafwijkingen van het gemiddelde),

Een videodemo van de toepassing ervan staat hier,

Wat is het addertje onder het gras? Waarom gebruiken mensen deze ‘meer universele’ regel niet?

Het is duidelijk wat het addertje onder het gras is als je naar de tabel of de wiskundige definitie kijkt. De Chebyshev-regel is veel zwakker dan de Gaussiaanse regel wat betreft het stellen van grenzen aan de gegevens.

Hij volgt een 1/k²-patroon in vergelijking met een exponentieel dalend patroon voor de Normale verdeling.

Bijv. om iets met 95% betrouwbaarheid te begrenzen, moet je gegevens tot 4,5 standaarddeviaties opnemen vs.

Maar het kan nog steeds de dag redden als de gegevens niet op een normale verdeling lijken.

Is er iets beters?

Er is een andere limiet genaamd, “Chernoff Bound”/Hoeffding ongelijkheid die een exponentieel scherpe staartverdeling geeft (in vergelijking met de 1/k²) voor sommen van onafhankelijke willekeurige variabelen.

Deze kan ook worden gebruikt in plaats van de Gaussische verdeling wanneer de gegevens er niet normaal uitzien, maar alleen wanneer we een hoge mate van vertrouwen hebben dat het onderliggende proces is opgebouwd uit subprocessen die volledig onafhankelijk van elkaar zijn.

In veel sociale en zakelijke gevallen zijn de uiteindelijke gegevens helaas het resultaat van een uiterst ingewikkelde interactie van vele subprocessen die onderling sterk afhankelijk kunnen zijn.

Samenvatting

In dit artikel hebben we geleerd over een bepaald type statistische limiet die kan worden toegepast op de breedst mogelijke verdeling van gegevens, onafhankelijk van de aanname van Normaliteit. Dit komt van pas wanneer we weinig weten over de werkelijke bron van de gegevens en niet kunnen aannemen dat deze een Gaussische verdeling volgen. De limiet volgt een machtswet in plaats van een exponentieel karakter (zoals bij het Gaussisch) en is daarom zwakker. Maar het is een belangrijk instrument om in uw repertoire te hebben voor het analyseren van elke willekeurige soort van gegevensverdeling.