Som Van Product (SOP) & Product Van Som (POS)
On november 10, 2021 by adminProduct Van Som (POS) &Som Van Product (SOP)
Inhoudsopgave
Som Van Product (SOP)
Som Van Product is de afgekorte vorm van SOP. Som van productvorm is een uitdrukkingsvorm in Booleaanse algebra waarin verschillende producttermen van ingangen bij elkaar worden opgeteld. Dit product is geen rekenkundige vermenigvuldiging, maar het is Booleaans logisch EN en de Som is Booleaans logisch OF.
Om SOP beter te begrijpen, moeten we weten wat min term is.
Min Term
Minterm betekent de term die waar is voor een minimum aantal combinaties van ingangen. Dat is waar voor slechts één combinatie van ingangen.
Omdat AND-poorten ook alleen waar zijn als alle ingangen waar zijn, kunnen we zeggen dat mintermen AND van ingangscombinaties zijn, zoals in de onderstaande tabel.
3 ingangen hebben 8 verschillende combinaties. Elke combinatie heeft een mintermen, aangeduid met kleine m en het decimale combinatiegetal geschreven in subscript. Elk van deze mintermen zal alleen waar zijn voor de specifieke ingangscombinatie.
- Je kunt ook lezen: Digitale Asynchrone Teller (Ripple Counter) – Soorten, Werking & Toepassing
Soorten Sum Of Product (SOP) Vormen
Er zijn een paar verschillende vormen van Sum of Product.
- Canonieke SOP-vorm
- Non-Canonieke SOP-vorm
- Minimale SOP-vorm
Canonieke SOP-vorm
Dit is de standaardvorm van Som van Product. Zij wordt gevormd door O Ring de mintermen van de functie waarvoor de uitkomst waar is. Dit is ook bekend als Som van Min termen of Canonieke disjunctieve normale vorm (CDNF). Het is gewoon een mooie naam. “Canonical” betekent “gestandaardiseerd” en “disjunctive” betekent “Logical OR union”.
Canonieke SOP expressie wordt weergegeven door sommatieteken ∑ en mintermen in de accolades waarvoor de output waar is.
Voor een functie is hieronder bijvoorbeeld de waarheidstabel gegeven.

Voor deze functie is de canonieke SOP-uitdrukking
F = ∑( m1, m2, m3, m5 )
Wat betekent dat de functie waar is voor de mintermen {1, 2, 3, 5}.
Door de sommatie uit te breiden krijgen we.
F = m1 + m2 + m3 + m5
Nu de mintermen in de uitdrukking zetten
F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C
Canonieke vorm bevat alle ingangen aangevuld of niet aangevuld in zijn producttermen.
U kunt ook lezen: Digitale Synchrone Teller – Soorten, Werking & Toepassingen
Niet-kanonieke SOP-vorm
Zoals de naam al aangeeft, is deze vorm de niet-gestandaardiseerde vorm van SOP-expressies. De producttermen zijn niet de mintermen, maar ze zijn vereenvoudigd. Laten we de bovenstaande functie in de canonieke vorm als voorbeeld nemen.
F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C
F = A̅B̅C + A̅B(C̅ + C) + AB̅C
F = A̅B̅C + A̅B(1) + AB̅C
F = A̅B̅C + A̅B + AB̅C
Deze uitdrukking is nog steeds in Som van Product vorm, maar het is nietcanonieke of niet-gestandaardiseerde vorm.
Minimale SOP-vorm
Deze vorm is de meest vereenvoudigde SOP-uitdrukking van een functie. Het is ook een vorm van niet-canonieke vorm. Minimale SOP-vorm kan worden gemaakt met behulp van Booleaanse algebraïsche stellingen, maar het is zeer gemakkelijk gemaakt met behulp van Karnaugh map (K-map).
Minimale SOP-vorm heeft de voorkeur omdat het het minimum aantal poorten en invoerlijnen gebruikt. het is commercieel voordelig vanwege zijn compacte afmetingen, snelle snelheid, en lage fabricagekosten.
Laten we een voorbeeld nemen van de hierboven gegeven functie in canonieke vorm.

De K-map ervan is hieronder gegeven.
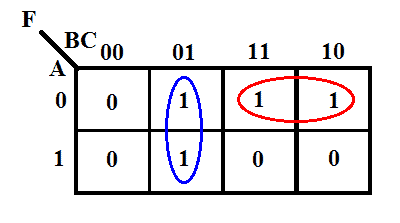
Volgens de K-map wordt de uitgangsuitdrukking
F = B̅C + A̅B
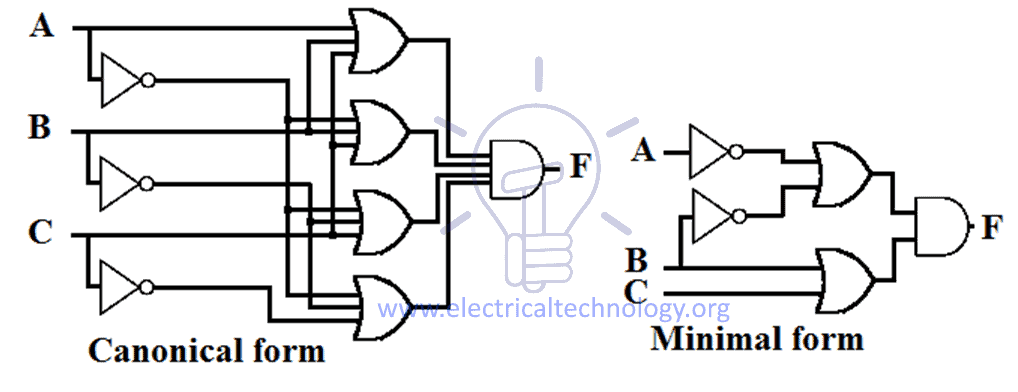
Dit is de meest vereenvoudigde & geoptimaliseerde uitdrukking voor de genoemde functie. Deze uitdrukking vereist slechts twee 2-input AND poorten & één 2-input OR poort. De canonieke vorm heeft echter vier 3-input AND gates & één 4-input OR gate nodig, wat relatief duurder is dan de implementatie in de minimale vorm.
- Je kunt ook lezen: Ringteller & Johnson Counter – Constructie & Werking
Schematisch ontwerp van Sum Of Product (SOP)
SOP expressie implementeert 2-niveau AND-OR ontwerp waarin het 1e niveau poort is AND poort na het 2e niveau poort die OR-poort is. Voor het schematische ontwerp van een SOP-uitdrukking is een groepsarray van AND-poorten & één OR-poort nodig.
Elke SOP-uitdrukking heeft min of meer hetzelfde ontwerp, d.w.z. dat alle ingangen door AND-poorten gaan en dat vervolgens de uitgang van deze AND-poorten door een OR-poort gaat, zoals in de onderstaande figuur is weergegeven.
Het aantal ingangen en het aantal AND-poorten is afhankelijk van de uitdrukking die men implementeert.
Voorbeeld van ontwerpen van canonieke en minimale SOP-uitdrukking voor een functie is hieronder gegeven.
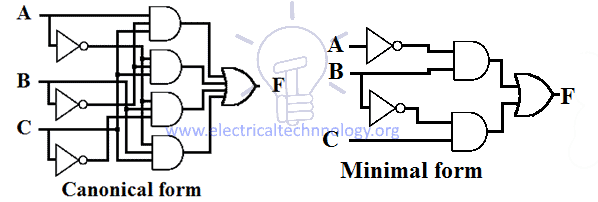
Conversie van Minimale SOP naar Canonieke SOP-vorm
Conversie van minimale of enige vorm van niet-canonieke vorm naar canonieke vorm is heel eenvoudig.
Zoals we weten heeft de canonieke vorm mintermen & mintermen bestaan uit alle ingangen, aangevuld of niet-gecomplementeerd. Dus zullen we elke term van minimale SOP vermenigvuldigen met de som van de ontbrekende inputs aangevuld en niet-aangevuld. Voorbeeld van conversie voor de bovenstaande functie in minimale SOP-vorm is hieronder gegeven.
Minimale SOP-vorm
F = A̅B + B̅C
De term A̅B mist ingang C. Dus zullen we A̅B vermenigvuldigen met (C+C̅) omdat (C+C̅ = 1). De term B̅C mist ingang A. dus wordt deze vermenigvuldigd met (A+A̅)
F = A̅B(C + C̅) + B̅C(A + A̅)
F = A̅BC + A̅BC̅ + AB̅C + A̅B̅C
Nu is deze uitdrukking in de canonieke vorm.
Conversie van Canonieke SOP naar Canonieke POS
Standaard SOP-uitdrukking kan worden omgezet in standaard POS (product of sum)-uitdrukking. Bijvoorbeeld, de hierboven gegeven functie is in canonieke SOP-vorm
F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C
F = ∑ ( m1, m2, m3, m5 )
De resterende termen van deze functie zijn maxtermen waarvoor de uitvoer vals is. Deze max termen zijn M0,M4,M6,M7. Deze maxtermen zullen in de POS-expressie worden gebruikt als het product van deze maxtermen. Het symbool van Product is ∏.
F = ∏ ( M0, M4, M6, M7)
F = (A+B+C)(A̅+B̅+C)(A̅+B̅+C)(A̅+B̅+C̅)
De Max-termen zijn het complement van mintermen. Daarom is M0=(A+B+C).
- Je kunt ook lezen: Ripple Carry And Carry Look Ahead Adder
Conversie van Canonieke SOP naar Minimale SOP
Canonieke SOP kan worden geconverteerd naar minimale SOP. Het kan worden omgezet met behulp van Karnaugh map of Booleaanse algebraïsche stellingen. De K-map methode is zeer eenvoudig en het voorbeeld ervan is hierboven gedaan in de minimale SOP vorm.
Product of Sum
Product of Sum afgekort voor POS.
De product of Sum vorm is een vorm waarin producten van verschillende somtermen van ingangen worden genomen. Dit zijn geen rekenkundig product en som, maar het zijn logische Booleaanse AND en OR respectievelijk.
Om het Product van Som beter te begrijpen, moeten we weten over Max term.
Max Term
Maxterm betekent de term of uitdrukking die waar is voor een maximaal aantal ingangscombinaties of die onwaar is voor slechts één combinatie van ingangen.
Omdat OR gate ook onwaar geeft voor slechts één ingangscombinatie. Maxterm is dus OR van ofwel gecomplementeerde ofwel niet-gecomplementeerde inputs.
Maxtermen voor 3 inputvariabelen zijn hieronder gegeven.
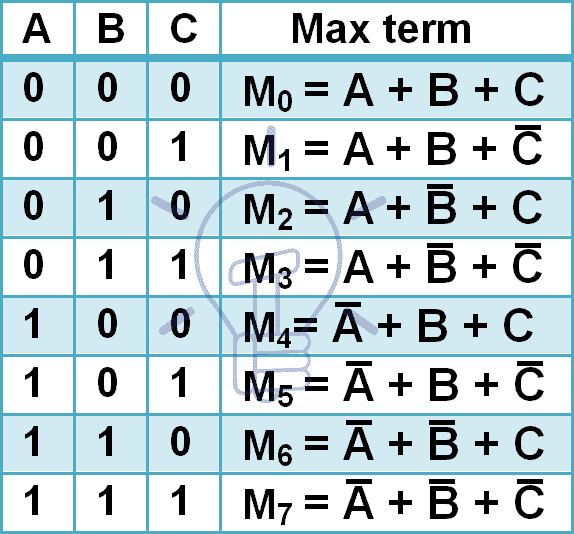
3 inputs hebben 8 verschillende combinaties, dus zal het 8 maxtermen hebben. Maxtermen worden aangeduid met een hoofdletter M en een decimaal combinatiegetal in het subscript, zoals in de bovenstaande tabel is aangegeven.
In maxterm wordt elke input aangevuld, omdat Maxterm alleen ‘0’ geeft wanneer de genoemde combinatie wordt toegepast en Maxterm het complement is van minterm.
M3 = m̅3
M3 = (A̅BC)’
M3 = A + B̅ +C̅ DE wet van Morgan
Waarom voor A=0 Max term bestaat uit A & voor A=1 Max term bestaat uit A̅.
Je kunt ook lezen: Digitale Flip-Flops – SR, D, JK en T Flip Flops
Soorten Product Of Sum-vormen
Er zijn verschillende soorten Product Of Sum-vormen.
- Canonieke POS-vorm
- Niet – Canonieke vorm
- Minimale POS-vorm
Canonieke POS-vorm
Het is ook bekend als Product van Max term of Canonieke conjunctieve normale vorm (CCNF). Canoniek betekent standaard en conjunctief betekent snijpunt.
In deze vorm zijn de Maxtermen samen AND waarvoor de uitvoer onwaar is.
Canonieke POS-uitdrukking wordt weergegeven door ∏ en de Maxtermen waarvoor de uitvoer onwaar is tussen haakjes, zoals in het onderstaande voorbeeld.

F = ∏ (M0, M4, M6, M7)
Uitbreiding van het product
F = M0.M4.M6.M7
Plaatsing van Max termen
F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)
De canonieke vorm bevat alle ingangen aangevuld of niet-gecomplementeerd in zijn elke Som term.
- Je kunt ook lezen: Clap Switch Circuit Electronic Project Using 555 Timer
Non – Canonical Form
Het product van som expressie die niet in standaard vorm wordt genoemd niet-canonieke vorm.
Let’s nemen de hierboven gegeven functie als een voorbeeld.
F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)
F = (B+C) (A̅+B̅+C)(A̅+B̅+C̅)
Zelfde maar omgekeerde termen elimineren uit twee Max termen en vormen een enkele term om het te bewijzen hier is een voorbeeld.
= (A+B+C) (A̅+B+C)
= AA̅+AB+AC+A̅B+BB+BC+A̅C+BC+CC
= 0+AB+AC+A̅B+A̅C+B+BC+C
= A(B+C)+A̅(B+C)+B(1+C)+C
= (B+C)(A+A̅)+B(1)+C
= (B+C)(0)+B+C
= B+C
De bereikte uitdrukking is nog steeds in Product of Sum vorm, maar het is nietcanonieke vorm.
Minimale POS-vorm
Dit is de meest vereenvoudigde en geoptimaliseerde vorm van een POS-uitdrukking die niet-canoniek is. De minimale Product of Sum-vorm kan worden bereikt met behulp van Booleaanse algebraïsche stellingen, zoals in het hierboven gegeven niet-canonieke voorbeeld. Een andere methode om de minimale POS vorm te bereiken is door gebruik te maken van Karnaugh map, hetgeen relatief eenvoudiger is dan het gebruik van Booleaanse algebraïsche stellingen.
De minimale POS vorm gebruikt minder ingangen en logische poorten tijdens de implementatie, daarom wordt aan deze vorm de voorkeur gegeven boven de canonieke vorm vanwege hun compacte, snelle en goedkope implementatie.
Laten we de hierboven gegeven functie als voorbeeld nemen
K-map van de functie
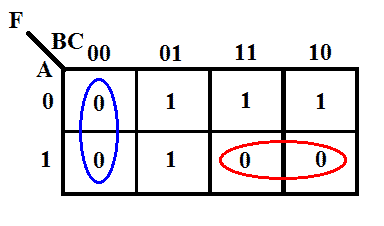
Minimale uitdrukking met behulp van K-map
F = (B+C) (A̅+B̅)
De bereikte uitdrukking is de minimale product van som-vorm. Het is nog steeds een Product of Sum uitdrukking, maar het heeft slechts 2 ingangen twee OR poorten en een enkele 2 input AND poort nodig. De canonieke vorm heeft echter 4 OR poorten van 3 ingangen en 1 AND poort van 4 ingangen nodig.
- Je kunt ook lezen: Negative Feedback and Negative Feedback Amplifier Systems
Schematisch ontwerp van Product of Sum (POS)
De uitdrukking Product of Sum heeft een specifiek schematisch ontwerp van OR-AND. In OR-AND gaan de ingangen door een reeks OR-poorten die het eerste niveau van poorten vormen, de uitgang van het eerste niveau OR-poorten gaat door het tweede niveau van de poort, die een AND-poort is.
Het aantal ingangen en het aantal poorten dat in dit ontwerp wordt gebruikt, hangt af van de uitdrukking die moet worden geïmplementeerd.
De canonieke vorm bestaat uit het maximale aantal mogelijke ingangen en poorten, de minimale vorm bestaat echter uit het laagst mogelijke aantal ingangen en poorten. Het schematische ontwerp van de canonieke en minimale POS-vorm wordt hieronder gegeven.
Conversie van Minimale POS naar Canonieke vorm POS
Zoals we weten heeft de canonieke vorm van POS max termen en bevatten max termen elke invoer, aangevuld of niet-gecomplementeerd. Dus zullen we elke somterm toevoegen met het product van de gecomplementeerde en de niet-gecomplementeerde ontbrekende invoer. Voorbeeld van de omzetting is hieronder gegeven.
Minimale POS vorm
F = (A̅+B̅) (B+C)
(A̅+B̅) term is ontbrekende C invoer, dus voegen we (CC̅) er aan toe. (B+C) term mist A ingang dus we voegen (AA̅) er aan toe.
F = (A̅+B̅+CC̅) (B+C+AA̅)
F = (A̅+B̅+C)(A̅+B̅+C̅)(A+B+C)
Deze uitdrukking is nu in canonieke vorm.
- Je kunt ook lezen: Teller en soorten elektronische tellers
Conversie van Canonieke POS naar SOP
Het product van Som-uitdrukking kan alleen in Som van Product-vorm worden geconverteerd als de uitdrukking in canonieke vorm is. Canonieke POS en canonieke SOP zijn onderling converteerbaar, d.w.z. zij kunnen in elkaar worden omgezet. Hieronder volgt een voorbeeld van POS naar SOP conversie.
POS canonieke vorm
F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)
In de canonieke vorm is elke somterm een max term, zodat hij ook geschreven kan worden als:
F = ∏(M0,M4,M6,M7)
De resterende combinaties van ingangen zijn mintermen van de functie waarvoor de output waar is. Om deze om te zetten in een SOP-uitdrukking veranderen we eerst het symbool in een sommatie (∑) en gebruiken we de overblijvende minterm.
F = ∑ (m1,m2,m3,m5)
Nu breiden we het sommatieteken uit tot een canonieke SOP-uitdrukking.
F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C
Min termen zijn complement van Max termen voor dezelfde combinatie van ingangen.
Canoniek naar Minimaal POS
Een canoniek Product van Som uitdrukking kan worden omgezet in Minimaal Product van som vorm door gebruik te maken van Karnaugh map (K-map). Een andere methode voor het omzetten van canoniek in minimaal is met behulp van Booleaanse algebraïsche stellingen.
Het gebruik van K-map is zeer eenvoudig en daarom wordt de voorkeur gegeven aan K-map. Voor een minimale POS-uitdrukking worden de 0’s in K-map gecombineerd tot groepen en de uitdrukking die we krijgen wordt aangevuld omdat de groepen uit ‘0’s’ bestaan. Het voorbeeld is hierboven gedaan.
U kunt ook lezen:
- Digital Logic NOT Gate – Digital Inverter Logic Gate
- Exclusive-NOR (XNOR) Digital Logic Gate
- Digital Logic NOR Gate
- Digital Logic NAND Gate
Geef een antwoord