Omtrek van een Cirkel – Uitleg & Voorbeelden
On januari 21, 2022 by adminWe hebben eerder gezien hoe we de omtrek van een veelhoek kunnen vinden. We weten dat een cirkel geen veelhoek is en dus ook geen omtrek heeft. We gebruiken een equivalente vorm voor een cirkel, genaamd omtrek.
In dit artikel gaan we bespreken hoe de omtrek van een cirkel te vinden, formule voor omtrek van cirkel en voorbeeldproblemen over de omtrek van een cirkel.
Wat is de omtrek van een cirkel?
De afstand rond een veelhoek zoals een vierkant of rechthoek wordt de omtrek (P) genoemd. De afstand rond een cirkel daarentegen wordt de omtrek (C) genoemd. De omtrek van een cirkel is dus de lineaire afstand van een rand van de cirkel.
Waarom moeten we de omtrek van een cirkel berekenen?
De omtrek van een object bepalen is belangrijk in de volgende scenario’s:
Of u nu een beha, broek of trui wilt kopen, u moet de afstand rond uw taille of borst weten. Hoewel uw lichaam geen perfecte cirkel is, moet u de omtrek meten met een meetlint. Kleermakers gebruiken deze techniek meestal om de omtrek van een jurk te bepalen.
U moet ook de omtrek van een cirkel weten als u knutselt, een hekwerk rond uw bubbelbad plaatst of gewoon een wiskundeprobleem voor school oplost.
Hoe vind je de omtrek van een cirkel?
Zoals eerder gezegd, is de omtrek of omtrek van een cirkel de afstand rond een cirkel of een cirkelvorm. De omtrek van een cirkel is gelijk aan de lengte van een rechte lijn die gevouwen of gebogen is om de cirkel te maken. De omtrek van een cirkel wordt gemeten in meters, kilometers, yards, inches enz.
Er zijn twee manieren om de omtrek of omtrek van een cirkel te vinden. Bij de eerste formule wordt de straal gebruikt en bij de tweede de diameter van een cirkel. Het is belangrijk op te merken, dat beide methoden hetzelfde resultaat opleveren.
Laten we eens kijken.
De omtrek van een cirkel wordt gegeven door;
C = 2 * π* R = 2πR
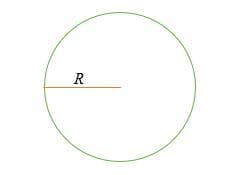
waar,
C = omtrek of perimeter,
R = de straal van een cirkel,
π = de wiskundige constante bekend als Pi
Of
C = π* D = π D
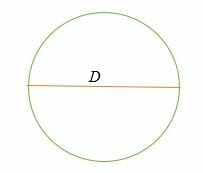
waar, D = 2R = de diameter van een cirkel
Voor elke cirkel is de verhouding tussen de omtrek en de diameter gelijk aan een constante bekend als pi.
Omtrek/Diameter = Pi
C /D = Pi of C/2R = pi
De geschatte waarde van pi (π) = 22/7 = 3,1415926535897…. (een niet-aflopende waarde)
Om de omtrek van een cirkel gemakkelijker te kunnen berekenen, wordt de waarde van pi op 3,14 gesteld (π = 3,14).
Laten we hieronder een paar voorbeelden zien om het begrip omtrek op te poetsen.
Voorbeeld 1
Vind de omtrek van de cirkel met een straal van 8 cm.
Oplossing
Omtrek = 2 * π* R = 2πR
= 2 * 3,14 * 8
= 50,24 cm.
Voorbeeld 2
Bereken de omtrek van een cirkel met een diameter van 70 mm
Oplossing
Omtrek = π* D = π D
= 3,14 * 70
= 219.8 mm
Voorbeeld 3
Bereken de omtrek van een cirkelvormige bloementuin waarvan de straal 10 m is.
Oplossing
Omtrek = 2 * π* R = 2πR
= 2 * 3,14 * 10
= 62,8 m.
Voorbeeld 4
De omtrek van een cirkel is 440 yards. Bereken de diameter en de straal van de cirkel.
Oplossing
Omtrek = 2 * π* R = 2πR
440 =2 * 3,14 * R
440 = 6.28R
Deel beide zijden door 6,28 om te krijgen,
R = 70,06
Daaruit volgt dat de straal van de cirkel 70,06 yards is. Maar omdat de diameter tweemaal de straal van een cirkel is, is de diameter dus gelijk aan 140,12 yards.
Voorbeeld 5
De diameter van de wielen van een fiets is 100 cm. Hoeveel omwentelingen zal elk wiel maken om een afstand van 157 meter af te leggen
Oplossing
Bereken de omtrek van het wiel van de fiets.
Omtrek = π D
= 3.14 * 100
= 314 cm
Om het aantal omwentelingen van het wiel te krijgen, deelt u de afgelegde afstand door de omtrek van het wiel.
We moeten 157 meter omzetten in cm voordat we delen, dus we vermenigvuldigen 157 met 100 om 15700 cm te krijgen. Daarom,
Aantal omwentelingen = 15700 cm/314 cm
= 50 omwentelingen.
Voorbeeld 6
Een stuk van een draad in de vorm van een rechthoek van lengte 100 cm en breedte 50 cm wordt afgeknipt en gevouwen tot een cirkel. Bereken de omtrek en de straal van de gevormde cirkel.
Oplossing
De omtrek van de gevormde cirkel = de omtrek van de rechthoekige draad.
Omtrek van een rechthoek = 2(L + B)
= 2(100 + 50) cm
= 2 * 150 cm
= 300 cm.
De omtrek van de cirkel zal dus 300 cm zijn.
Nu de straal berekenen.
Omtrek = 2 π R
300 cm = 2 * π * R
300 cm = 2 * 3,14 * R
300 cm = 6,28R
Deel beide zijden door 6,28.
R = 47.77 cm
Dus de straal van de cirkel wordt 47,77 cm.
Voorbeeld 7
De straal van elk wiel van een motorfiets is 0. 85 m. Hoe ver zal de motorfiets zich verplaatsen als elk wiel 1000 omwentelingen maakt. Neem aan dat de motorfiets zich op een rechte lijn voortbeweegt.
Oplossing
Vind eerst de omtrek van het wiel.
Omtrek = 2 π R
= 2 * 3,14 * 0,85
= 5,338 m.
Om de afgelegde afstand te vinden, vermenigvuldigt men de omtrek van het wiel met het aantal gemaakte omwentelingen.
Afstand = 5,338 * 1000
= 5338 m
De afgelegde afstand is dus gelijk aan 5,338 kilometer.
Praktijkvragen
- Een 12-incher pizza wordt aan Mike en zijn vrienden geserveerd. Mike is geïnteresseerd in het berekenen van de omtrek. Help hem!
- De omtrek van een bepaald vierkant is 1/3e van de oppervlakte van een bepaalde cirkel. Als de lengte van het vierkant L eenheden is, bepaal dan de diameter van de cirkel in termen van L.
Antwoorden
- 12π inches of 37,67 inches
- 12L/π eenheden
Geef een antwoord