Functions or Mapping

Nu, in functies of mapping gaan we speciale soorten relaties bestuderen die functies of mapping worden genoemd. Om deze te begrijpen, nemen we enkele voorbeelden uit het echte leven.

Al deze vragen hebben
unieke antwoorden. Laten we
kijken hoe we
dit kunnen relateren in learning mapping.

● Waar komt de zon op?

Oost

● Wat is de hoofdstad van India?

Delhi

● Wat is de opvolger van 4?

5

●● Wat is de som van 5 en 3?

8

Mapping of Functies:

Als A en B twee niet-lege verzamelingen zijn, dan wordt een relatie ‘f’ van verzameling A naar verzameling B een functie of mapping genoemd,
●als elk element van verzameling A geassocieerd is met uniek element van verzameling B.

● De functie ‘f’ van A naar B wordt aangeduid met f : A → B.

● Als f een functie is van A naar B en x ∈ A, dan is f(x) ∈ B waarbij f(x) het beeld van x onder f wordt genoemd en x het prebeeld van f(x) onder ‘f’.

Note:

Om ervoor te zorgen dat f een afbeelding is van A naar B:

● Elk element van A moet een afbeelding in B hebben. De aangrenzende figuur geeft geen afbeelding weer, omdat het element d in verzameling A niet geassocieerd is met een element van verzameling B.

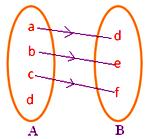
● Geen enkel element van A mag meer dan één afbeelding hebben. De aangrenzende figuur geeft geen afbeelding weer, aangezien element b in verzameling A geassocieerd is met twee elementen d, f van verzameling B.

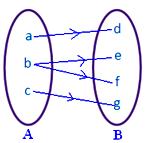
● Verschillende elementen van A kunnen in B hetzelfde beeld hebben. De aangrenzende figuur geeft een afbeelding weer.

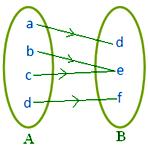
Noot:

Elke afbeelding is een relatie, maar elke relatie is niet noodzakelijkerwijs een afbeelding.

Functie als een speciale soort relatie:

Laten we de functie als een speciale soort relatie eens in herinnering roepen en bekijken Stel, A en B zijn twee niet-lege verzamelingen, dan wordt een regel ‘f’ die elk element van A met een uniek element van B associeert een functie of een afbeelding van A naar B genoemd.
Als ‘f’ een afbeelding is van A naar B,

drukken we het uit als f: A → B

we lezen het als ‘f’ is een functie van A naar B.
Als ‘f ‘ een functie is van A naar B en x∈A en y∈B, dan zeggen we dat y het beeld is van element x onder de functie ‘ f ‘ en duiden we het aan met f(x).
Daarom schrijven we het als y = f(x)

Hierbij wordt element x het voorbeeld van y genoemd.

Dus, voor een functie van A naar B.
● moeten A en B niet-leeg zijn.

● Elk element van A moet een beeld in B hebben.

● Geen enkel element van “A” mag meer dan één beeld in “B” hebben.
Note:

● Twee of meer elementen van A kunnen hetzelfde beeld in B hebben.

● f : x → y betekent dat onder de functie van ‘f’ van A naar B, een element x van A beeld y in B heeft.

● Het is noodzakelijk dat elk f-beeld in B is, maar er kunnen enkele elementen in B zijn die geen f-beelden zijn van enig element van A.

● Relaties en toewijzingen

Geordend paar

Cartesisch product van twee verzamelingen

Relatie

Domein en bereik van een relatie

Functies of toewijzingen

Domein Co-domein en bereik van een functie

●Relaties en Mapping – Werkbladen

Werkblad over wiskundige relaties

Werkblad over functies of mapping

7e graad wiskundeproblemen

8e graad wiskundepraktijk
Van Functies of Mapping naar HOME PAGE