2.12: Vergelijking van Van der Waals

Een vergelijking van Van der Waals breidt de ideale gasvergelijking op een eenvoudige manier uit. De vergelijking van Van der Waals is

Deze vergelijking past beter bij druk-volume-temperatuurgegevens voor een echt gas dan de ideale gasvergelijking doet. De betere passing wordt verkregen door twee parameters (aangeduid met “a” en “b”) in te voeren die voor elk gas experimenteel moeten worden bepaald. De vergelijking van Van der Waals is bijzonder nuttig in onze pogingen om het gedrag van echte gassen te begrijpen, omdat zij een eenvoudig fysisch beeld geeft van het verschil tussen een echt gas en een ideaal gas.

Bij het afleiden van de wet van Boyle uit de wetten van Newton, nemen we aan dat de gasmoleculen niet met elkaar interageren. Eenvoudige argumenten tonen aan dat dit slechts bij benadering waar kan zijn. Echte gasmoleculen moeten wel met elkaar interageren. Op korte afstanden stoten ze elkaar af. Op wat grotere afstanden trekken ze elkaar aan. De ideale gasvergelijking kan ook worden afgeleid uit de basisaannamen die we in §10 maken, door een toepassing van de theorie van de statistische thermodynamica. Door verschillende aannamen te doen over de eigenschappen van moleculen, kunnen we de statistische thermodynamica toepassen om de van der Waals vergelijking af te leiden. De vereiste aannamen zijn dat de moleculen een eindig volume innemen en dat zij elkaar aantrekken met een kracht die varieert als het omgekeerde van een macht van de afstand tussen hen. (De aantrekkingskracht wordt meestal evenredig verondersteld met r^{-6})

Om in te zien dat echte gasmoleculen elkaar zowel aantrekken als afstoten, hoeven we ons alleen maar te herinneren dat elk gas vloeibaar kan worden gemaakt door de temperatuur te verlagen en de druk te verhogen die erop wordt uitgeoefend. Als we de vloeistof verder afkoelen, bevriest hij tot een vaste stof. Twee kenmerken van een vaste stof zijn dat hij zijn vorm behoudt en dat hij bijna onsamendrukbaar is. Wij schrijven de samendrukbaarheid van een vaste stof toe aan de afstotende krachten tussen de samenstellende moleculen; zij zijn zo dicht bij elkaar gekomen dat de afstotende krachten tussen hen belangrijk zijn geworden. Om de vaste stof samen te drukken, moeten de moleculen nog dichter bij elkaar worden geduwd, wat een buitensporige kracht vereist. Aan de andere kant, als we een ijsblokje door de kamer gooien, vliegen alle samenstellende watermoleculen samen door de kamer. Het is duidelijk dat de watermoleculen in de vaste stof door elkaar worden aangetrokken, anders zouden ze allemaal hun eigen weg gaan – het ijsblokje gooien zou zijn als het gooien van een handvol droog zand. Maar de watermoleculen zijn dezelfde moleculen, ongeacht de temperatuur of de druk, dus als er tussen hen in de vaste fase aantrekkende en afstotende krachten bestaan, moeten deze krachten ook aanwezig zijn in de vloeibare en de gasfase.

In de gasfase staan de moleculen ver uit elkaar; in de vloeibare of de vaste fase zitten ze opeengepakt. Bij het kookpunt is het volume van een vloeistof veel kleiner dan het volume van het gas waaruit zij is gecondenseerd. Bij het vriespunt verschilt het volume van een vaste stof slechts weinig van het volume van de vloeistof waaruit zij is bevroren, en het is zeker groter dan nul. Deze alledaagse waarnemingen zijn gemakkelijk te verklaren door aan te nemen dat elke molecule een karakteristiek volume heeft. Dit is dan weer een gevolg van de aard van de intermoleculaire krachten; het is duidelijk dat deze krachten sterker worden naarmate de afstand tussen een paar moleculen kleiner wordt. Aangezien een vloeistof of een vaste stof een welbepaald volume inneemt, moet de afstotende kracht sneller toenemen dan de aantrekkende kracht wanneer de intermoleculaire afstand klein is. Vaak is het nuttig te spreken over het molaire volume van een gecondenseerde fase. Met molair volume bedoelen we het volume van één mol van een zuivere stof. Het molaire volume van een gecondenseerde fase wordt bepaald door de intermoleculaire afstand waarop er een evenwicht is tussen intermoleculaire aantrekkingskrachten en afstotingskrachten.

In gecondenseerde fasen bevinden moleculen zich uiteraard zeer dicht bij elkaar. Als we aannemen dat de lege ruimten tussen de moleculen verwaarloosbaar zijn, is het volume van een gecondenseerde fase ongeveer gelijk aan het aantal moleculen in het monster vermenigvuldigd met het volume van een enkel molecuul. Het molaire volume is dan het getal van Avogadro maal het volume dat door één molecule wordt ingenomen. Als we de dichtheid, D, en de molaire massa, \(\overline{M}) weten, kunnen we het molaire volume, \(\overline{V}), vinden als

Het volume dat door een molecuul wordt ingenomen, V({}_{molecuul}), wordt

De druk en het volume die in de vergelijking van van der Waals voorkomen zijn de druk en het volume van het echte gas. We kunnen de termen in de vergelijking van van der Waals in verband brengen met de ideale gasvergelijking: Het is nuttig om de termen links(P+{an}^2}/{V^2}rechts)en links(V-nbrechts)te zien als de druk en het volume van een hypothetisch ideaal gas. Dat is

&=nRT \eind}

Dan hebben we

We leiden de ideale gasvergelijking af uit een model waarin de moleculen niet op elkaar inwerkende puntmassa’s zijn. Het volume van een ideaal gas is dus het volume dat wordt ingenomen door een gas waarvan de afzonderlijke moleculen geen volume hebben. Als de individuele moleculen van een reëel gas effectief een volume innemen dat gelijk is aan het volume dat zou worden ingenomen door niet op elkaar inwerkende puntmassa’s, dus het effectieve volume van de gasmoleculen zelf, dan nemen ze er ƒ(n) effectief een volume in

Volgens de vergelijking van Van der Waals is het volume van een reëel gas het volume dat zou worden ingenomen door niet op elkaar inwerkende puntmassa’s, dus ƒ(V_{ideaal gas}}, plus het effectieve volume van de gasmoleculen zelf. (Wanneer gegevens voor echte gasmoleculen worden aangepast aan de van der Waals vergelijking, is de waarde van V(b) meestal iets groter dan het volume dat wordt geschat op basis van de vloeistofdichtheid en het molecuulgewicht. Zie probleem 24.)

Zo hebben we

We kunnen dit opvatten als een logisch gevolg van attractieve interacties tussen de moleculen van het echte gas. Hieruit volgt dat de druk van het echte gas lager is dan de druk van het hypothetische ideale gas, en wel evenredig met de evenredigheidsconstante van a>0}. De evenredigheidsconstante is \(a). Aangezien \({n}/{V}) de molaire dichtheid (mol per volume-eenheid) van de gasmoleculen is, is het een maat voor de concentratie. Het aantal botsingen tussen moleculen van dezelfde soort is evenredig met het kwadraat van hun concentratie. (Hierop wordt nader ingegaan in de hoofdstukken 4 en 5.) Het is dus een maat voor de frequentie waarmee de echte gasmoleculen met elkaar in aanraking komen. Als ze elkaar aantrekken als ze dicht bij elkaar komen, moet het effect van deze aantrekking evenredig zijn met \({n}/{V}}rechts)}^2). De vergelijking van van der Waals is dus in overeenstemming met het idee dat de druk van een echt gas verschilt van de druk van het hypothetische ideale gas met een hoeveelheid die evenredig is met de frequentie en sterkte van aantrekkelijke interacties.

Maar waarom zouden aantrekkelijke interacties dit effect hebben; waarom zou de druk van het echte gas lager moeten zijn dan die van het hypothetische ideale gas? Misschien is de beste manier om een kwalitatief beeld te ontwikkelen de erkenning dat aantrekkelijke intermoleculaire krachten de neiging hebben om de gasmoleculen te doen samenklonteren. Het zijn immers deze aantrekkende krachten die ervoor zorgen dat de moleculen bij lage temperaturen samenklonteren tot een vloeistof. Boven het kookpunt beperkt het vermogen van de gasmoleculen om hun eigen weg te gaan de gevolgen van deze tendens; maar zelfs in het gas moeten de aantrekkingskrachten zodanig werken dat het volume dat door de moleculen wordt ingenomen, wordt verkleind. Aangezien het door het gas ingenomen volume wordt bepaald door de grootte van de houder – en niet door de eigenschappen van het gas zelf – komt deze neiging tot klonteren tot uiting in een afname van de druk.

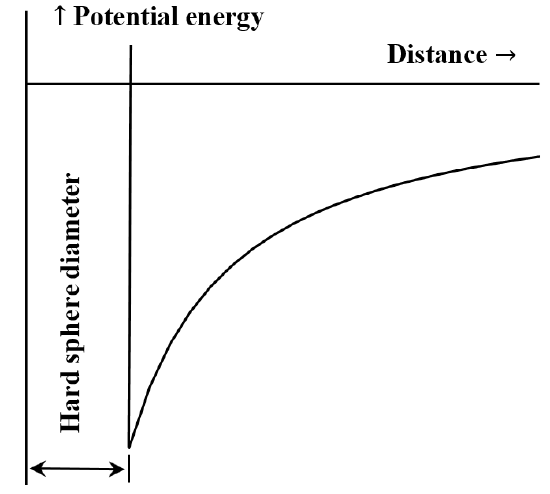
Het is vaak nuttig om de interactie tussen deeltjes of chemische samenstellingen te beschrijven in termen van een potentiaal-energie versus afstanddiagram. De van der Waals-vergelijking komt overeen met het geval dat de afstotende interactie tussen moleculen onbestaande is totdat de moleculen met elkaar in contact komen. Zodra ze elkaar raken, wordt de energie die nodig is om ze nog dichter bij elkaar te brengen willekeurig groot. Vaak wordt dit beschreven door te zeggen dat ze zich gedragen als “harde bollen”. De aantrekkingskracht tussen twee moleculen neemt af naarmate de afstand tussen hen groter wordt. Wanneer ze heel ver van elkaar verwijderd zijn, is de aantrekkingskracht heel klein. We zeggen dat de energie van de interactie nul is wanneer de moleculen oneindig ver van elkaar verwijderd zijn. Als we aanvankelijk twee ver van elkaar verwijderde, stilstaande, elkaar aantrekkende moleculen hebben, zullen zij spontaan naar elkaar toe bewegen, waarbij zij kinetische energie winnen. Hun potentiële energie neemt af naarmate ze elkaar naderen en bereikt zijn kleinste waarde wanneer de moleculen elkaar raken. De vergelijking van van der Waals impliceert dus het in figuur 5 geschetste diagram van de potentiële energie ten opzichte van de afstand.