Métodos de Pesquisa em Psicologia

O que é pesquisa correlacional?

Pesquisa correlacional é um tipo de pesquisa não experimental em que o pesquisador mede duas variáveis (binária ou contínua) e avalia a relação estatística (ou seja a correlação) entre elas com pouco ou nenhum esforço para controlar variáveis estranhas. Há muitas razões para que os pesquisadores interessados em relações estatísticas entre as variáveis optem por realizar um estudo correlacional ao invés de um experimento. A primeira é que eles não acreditam que a relação estatística é uma relação causal ou não estão interessados em relações causais. Recordar dois objetivos da ciência é descrever e prever e a estratégia da pesquisa correlacional permite aos pesquisadores alcançar ambos os objetivos. Especificamente, esta estratégia pode ser usada para descrever a força e a direção da relação entre duas variáveis e, se houver uma relação entre as variáveis, os pesquisadores podem usar pontuações em uma variável para prever pontuações na outra (usando uma técnica estatística chamada regressão, que é discutida mais adiante na seção sobre Correlação Complexa neste capítulo).

Uma outra razão pela qual os pesquisadores optariam por usar um estudo correlacional ao invés de um experimento é que a relação estatística de interesse é considerada causal, mas o pesquisador não pode manipular a variável independente porque é impossível, impraticável ou antiética. Por exemplo, enquanto um pesquisador pode estar interessado na relação entre a freqüência que as pessoas usam cannabis e suas habilidades de memória, eles não podem manipular eticamente a freqüência que as pessoas usam cannabis. Como tal, devem confiar na estratégia de pesquisa correlacional; devem simplesmente medir a frequência com que as pessoas usam cannabis e medir as suas capacidades de memória usando um teste de memória padronizado e depois determinar se a frequência com que as pessoas usam cannabis está estatisticamente relacionada com o desempenho do teste de memória.

A correlação também é usada para estabelecer a confiabilidade e validade das medições. Por exemplo, um pesquisador pode avaliar a validade de um breve teste de extração, administrando-o a um grande grupo de participantes, juntamente com um teste de extração mais longo que já demonstrou ser válido. Este investigador pode então verificar se os resultados dos participantes no teste breve estão fortemente correlacionados com os seus resultados no teste mais longo. Nenhum dos resultados do teste é considerado como causador do outro, portanto não há nenhuma variável independente a ser manipulada. Na verdade, os termos variável independente e variável dependente não se aplicam a este tipo de pesquisa.

Uma outra força da pesquisa correlacional é que ela é frequentemente mais alta em validade externa do que a pesquisa experimental. Lembre-se de que existe tipicamente um trade-off entre a validade interna e a validade externa. Como maiores controles são adicionados aos experimentos, a validade interna é aumentada, mas muitas vezes às custas da validade externa, já que são introduzidas condições artificiais que não existem na realidade. Em contraste, estudos correlacionais tipicamente têm baixa validade interna porque nada é manipulado ou controlado, mas muitas vezes têm alta validade externa. Uma vez que nada é manipulado ou controlado pelo experimentador, os resultados são mais propensos a refletir as relações que existem no mundo real.

Finalmente, estendendo-se sobre este compromisso entre validade interna e externa, a pesquisa correlacional pode ajudar a fornecer evidências convergentes para uma teoria. Se uma teoria é apoiada por um experimento verdadeiro que é alto em validade interna, bem como por um estudo correlacional que é alto em validade externa, então os pesquisadores podem ter mais confiança na validade de sua teoria. Como exemplo concreto, estudos correlacionais estabelecendo que existe uma relação entre ver televisão violenta e comportamento agressivo foram complementados por estudos experimentais confirmando que a relação é causal (Bushman & Huesmann, 2001).

A pesquisa correlacional sempre envolve variáveis quantitativas?

Um equívoco comum entre pesquisadores iniciantes é que a pesquisa correlacional deve envolver duas variáveis quantitativas, tais como pontuação em dois testes de conversão extra ou o número de aborrecimentos diários e o número de sintomas que as pessoas experimentaram. Entretanto, a característica que define a pesquisa correlacional é que as duas variáveis são medidas – qualquer uma delas é manipulada – e isto é verdade independentemente de as variáveis serem quantitativas ou categóricas. Imagine, por exemplo, que um pesquisador administre a Escala de Auto-Estima de Rosenberg para 50 estudantes universitários americanos e 50 estudantes universitários japoneses. Embora esta “sensação” seja uma experiência entre sujeitos, é um estudo correlacional porque o pesquisador não manipulou as nacionalidades dos estudantes. O mesmo acontece com o estudo de Cacioppo e Petty comparando professores universitários e operários de fábrica em termos de sua necessidade de conhecimento. É um estudo correlacional porque os pesquisadores não manipularam as ocupações dos participantes.

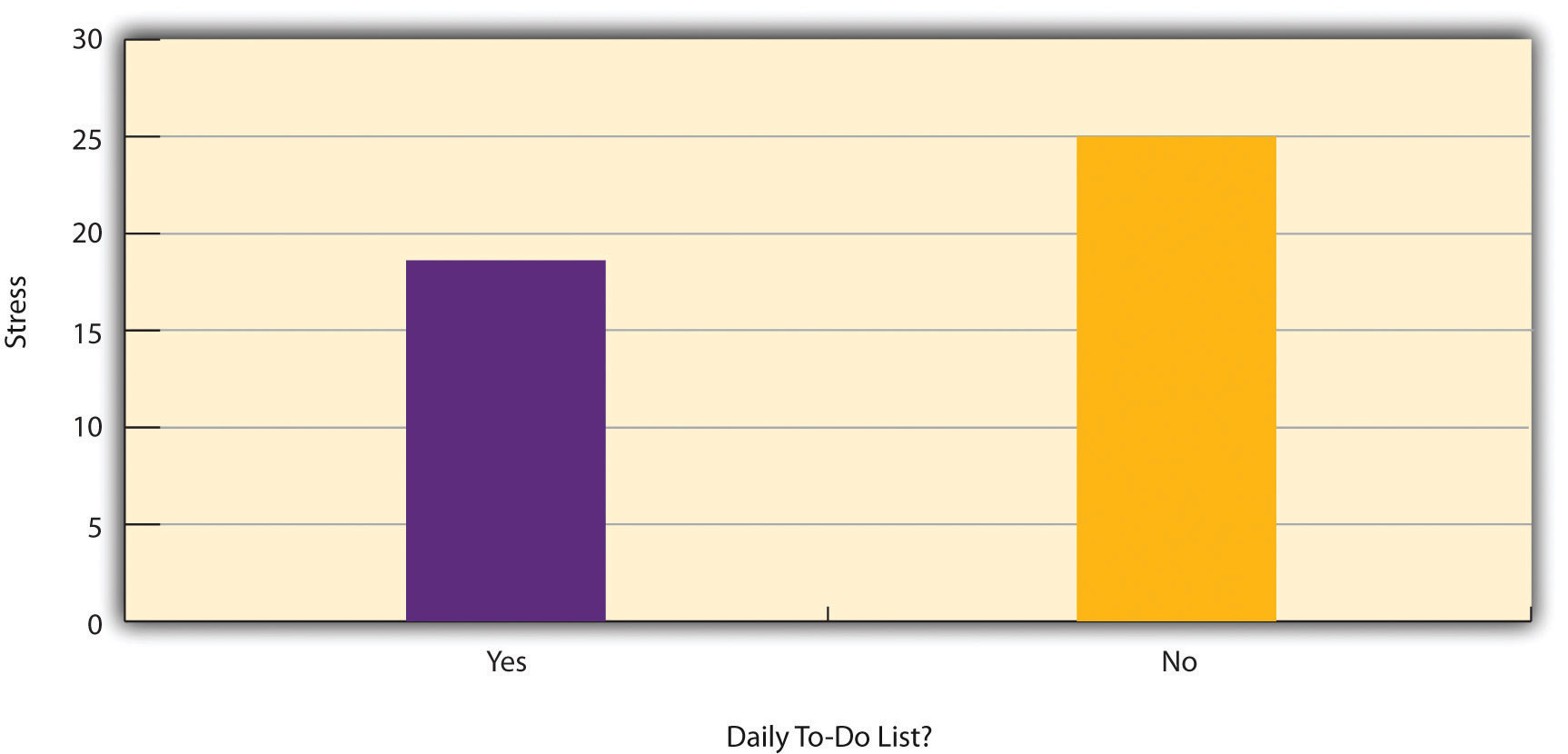
Figure 6.2 mostra dados de um estudo hipotético sobre a relação entre se as pessoas fazem uma lista diária de coisas a fazer (uma “lista de afazeres”) e o estresse. Note que não está claro se este é um experimento ou um estudo correlacional porque não está claro se a variável independente foi manipulada. Se o pesquisador designou aleatoriamente alguns participantes para fazer listas de coisas a fazer diariamente e outros não, então é um experimento. Se o pesquisador simplesmente perguntou aos participantes se eles fizeram listas de afazeres diários, então é um estudo correlacional. A distinção é importante porque se o estudo fosse uma experiência, então poderia concluir-se que fazer as listas diárias de afazeres reduziu o stress dos participantes. Mas se fosse um estudo correlacional, só se poderia concluir que estas variáveis estão estatisticamente relacionadas. Talvez o stress tem um efeito negativo sobre a capacidade das pessoas de planearem com antecedência (o problema de direccionalidade). Ou talvez as pessoas que são mais conscientes tenham mais probabilidade de fazer listas de tarefas e menos probabilidade de serem stressadas (o problema da terceira variável). O ponto crucial é que o que define um estudo como experimental ou correlacional não são as variáveis em estudo, nem se as variáveis são quantitativas ou categóricas, nem o tipo de gráfico ou estatística usada para analisar os dados. O que define um estudo é como o estudo é conduzido.

Recolha de Dados em Pesquisa Correlacional

Again, a característica definidora da pesquisa correlacional é que nenhuma das variáveis é manipulada. Não importa como ou onde as variáveis são medidas. Um pesquisador poderia fazer com que os participantes viessem a um laboratório para completar uma tarefa computadorizada de retrocesso de dígitos e uma tarefa computadorizada de tomada de decisão arriscada e depois avaliar a relação entre as pontuações dos participantes nas duas tarefas. Ou um pesquisador poderia ir a um shopping center para perguntar às pessoas sobre suas atitudes em relação ao ambiente e seus hábitos de compra e depois avaliar a relação entre essas duas variáveis. Ambos os estudos seriam correlacionais porque nenhuma variável independente é manipulada.

Correlações entre Variáveis Quantitativas

Correlações entre variáveis quantitativas são frequentemente apresentadas usando scatterplots. A Figura 6.3 mostra alguns dados hipotéticos sobre a relação entre a quantidade de pessoas sob estresse e o número de sintomas físicos que elas apresentam. Cada ponto no gráfico de dispersão representa a pontuação de uma pessoa em ambas as variáveis. Por exemplo, o ponto circulado na Figura 6.3 representa uma pessoa cujo escore de estresse era 10 e que tinha três sintomas físicos. Levando todos os pontos em consideração, pode-se ver que as pessoas sob mais estresse tendem a ter mais sintomas físicos. Este é um bom exemplo de uma relação positiva, na qual pontuações mais altas em uma variável tendem a ser associadas a pontuações mais altas na outra. Em outras palavras, eles se movem na mesma direção, tanto para cima quanto para baixo. Uma relação negativa é aquela em que pontuações mais altas em uma variável tendem a estar associadas a pontuações mais baixas na outra. Em outras palavras, eles se movem em direções opostas. Existe uma relação negativa entre estresse e funcionamento do sistema imunológico, por exemplo, porque maior estresse está associado a menor funcionamento do sistema imunológico.

A força de uma correlação entre variáveis quantitativas é tipicamente medida usando uma estatística chamada Coeficiente de Correlação de Pearson (ou r de Pearson). Como mostra a Figura 6.4, o r de Pearson varia de -1,00 (a relação negativa mais forte possível) a +1,00 (a relação positiva mais forte possível). Um valor de 0 significa que não há relação entre as duas variáveis. Quando o r de Pearson é 0, os pontos em um gráfico de dispersão formam uma “nuvem” sem forma. À medida que o seu valor se aproxima de -1,00 ou +1,00, os pontos aproximam-se cada vez mais de cair numa única linha recta. Coeficientes de correlação próximos a ±,10 são considerados pequenos, valores próximos a ±,30 são considerados médios e valores próximos a ±,50 são considerados grandes. Note que o sinal do r de Pearson não está relacionado com a sua força. Os valores de r de Pearson de +,30 e -,30, por exemplo, são igualmente fortes; é apenas que um representa uma relação positiva moderada e o outro uma relação negativa moderada. Com a excepção dos coeficientes de fiabilidade, a maioria das correlações que encontramos em Psicologia são pequenas ou moderadas em tamanho. O site http://rpsychologist.com/d3/correlation/, criado por Kristoffer Magnusson, proporciona uma excelente visualização interativa das correlações que permite ajustar a força e a direção de uma correlação ao mesmo tempo em que se assiste às mudanças correspondentes ao gráfico de dispersão.

Existem duas situações comuns em que o valor de r de Pearson pode ser enganoso. O r de Pearson é uma boa medida apenas para relações lineares, em que os pontos são melhor aproximados por uma linha recta. Não é uma boa medida para relações não lineares, em que os pontos são mais bem aproximados por uma linha curva. A Figura 6.5, por exemplo, mostra uma relação hipotética entre a quantidade de sono que as pessoas recebem por noite e o seu nível de depressão. Neste exemplo, a linha que melhor se aproxima dos pontos é uma curva – um tipo de “U” invertido – porque as pessoas que dormem cerca de oito horas tendem a ser as menos deprimidas. As que dormem muito pouco e as que dormem muito tendem a estar mais deprimidas. Embora a Figura 6.5 mostre uma relação bastante forte entre depressão e sono, o r de Pearson estaria perto de zero porque os pontos no “scatterplot” não estão bem ajustados por uma única linha reta. Isto significa que é importante fazer um gráfico de dispersão e confirmar que uma relação é aproximadamente linear antes de usar o r de Pearson. Relações não-lineares são bastante comuns em psicologia, mas medir sua força está além do escopo deste livro.

As outras situações comuns nas quais o valor do r de Pearson pode ser enganoso é quando uma ou ambas as variáveis têm uma faixa limitada na amostra em relação à população. Este problema é referido como restrição de faixa. Suponha, por exemplo, que existe uma forte correlação negativa entre a idade das pessoas e a sua apreciação da música hip hop, como mostra o gráfico da Figura 6.6. Pearson’s r aqui é -.77. No entanto, se coletássemos dados apenas de jovens de 18 a 24 anos – representados pela área sombreada da Figura 6.6 – então a relação pareceria bastante fraca. Na verdade, o r de Pearson para esta faixa restrita de idades é 0. É uma boa idéia, portanto, desenhar estudos para evitar a restrição da faixa. Por exemplo, se a idade é uma de suas variáveis primárias, então você pode planejar a coleta de dados de pessoas de uma ampla faixa etária. Como a restrição de faixa nem sempre é antecipada ou facilmente evitável, entretanto, é uma boa prática examinar seus dados para possível restrição de faixa e interpretar o r de Pearson à luz dos mesmos. (Há também métodos estatísticos para corrigir o r da Pearson para restrição de faixa, mas eles estão além do escopo deste livro).

Correlação Não Imply Causation

Você provavelmente já ouviu repetidamente que “Correlação não implica em causalidade”. Um exemplo divertido disso vem de um estudo de 2012 que mostrou uma correlação positiva (r de Pearson = 0,79) entre o consumo per capita de chocolate de uma nação e o número de prêmios Nobel concedidos aos cidadãos dessa nação. Parece claro, porém, que isso não significa que comer chocolate faça com que as pessoas ganhem prêmios Nobel, e não faria sentido tentar aumentar o número de prêmios Nobel ganhos recomendando que os pais alimentem seus filhos com mais chocolate.

Existem duas razões que essa correlação não implica em causalidade. A primeira é chamada de problema de direcionalidade. Duas variáveis, X e Y, podem estar estatisticamente relacionadas porque X causa Y ou porque Y causa X. Considere, por exemplo, um estudo mostrando que se as pessoas fazem ou não exercício está estatisticamente relacionado com o quão felizes estão – tal que as pessoas que fazem exercício são mais felizes, em média, do que as pessoas que não fazem. Essa relação estatística é consistente com a idéia de que o exercício físico causa felicidade, mas também é consistente com a idéia de que a felicidade causa exercício físico. Talvez ser feliz dê mais energia às pessoas ou as leve a procurar oportunidades de socializar com os outros, indo ao ginásio. A segunda razão pela qual a correlação não implica uma causa é chamada de problema da terceira variável. Duas variáveis, X e Y, podem ser estatisticamente relacionadas não porque X causa Y, ou porque Y causa X, mas porque alguma terceira variável, Z, causa X e Y. Por exemplo, o fato de que as nações que ganharam mais prêmios Nobel tendem a ter maior consumo de chocolate provavelmente reflete a geografia, já que os países europeus tendem a ter maiores taxas de consumo de chocolate per capita e a investir mais em educação e tecnologia (mais uma vez, per capita) do que muitos outros países do mundo. Da mesma forma, a relação estatística entre exercício e felicidade pode significar que alguma terceira variável, como a saúde física, causa ambas as outras. Ser fisicamente saudável pode fazer com que as pessoas façam exercício e sejam mais felizes. Correlações que são resultado de uma terceira variável são frequentemente referidas como correlações espúrias.

Alguns excelentes e divertidos exemplos de correlações espúrias podem ser encontrados em http://www.tylervigen.com (Figura 6.7 fornece um exemplo).