Articles

Formula for an Infinite Geometric Series
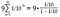
a=1/10, r=1/10 なので、aとrを組み合わせてn=1に調整すれば、この問題の元の総和と都合よく一致します。

Why Does 0.999… Equal 1?!
On 12月 6, 2021 by admin和の項について考えるもう一つの方法は、各連続項は前の項に共通の比率を掛けて得られるということです。
つまり、a/(1 – r) に収束する幾何級数があり、a は系列の最初の値、r は次の項を得るために乗ずる比率です。

シリーズの収束は、単に、シリーズに項を追加していくと、特定の値にどんどん近づいていくことを意味しています。 系列は収束値に無限に近づいていくのです。 無限のスケールでは、収束は等式になる。
この場合、1/10から始めて毎回1/10を掛けるので、aもrも1/10である。
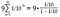
右辺の演算を完成させる。

さて、これで正式に0.999…は 1 に収束する、または等しくなることを正式に示しました。
最後に思うこと & Inspiration
これがあなたにとって奇妙に感じられたら、それは良いことです!
は、「1. 2つの異なる数字が、実際には異なる数字であるべきだということを、あなたは知っているのです。 この問題の直感に反する性質は、無限を扱うことに伴う奇妙さに固有のものです。
このような単純な問題であっても、人間の脳にとって目に見える範囲から、ある意味で我々の理解を超えた規模に移行しているのです。 有限の存在である私たちは、無限や永遠という概念を理解することはできても、それを本当に経験することはできません。
簡単に発見・再現できる数学から、心の中でテストし想像するしかないものへの移行を受け入れることは、数学の美しさと驚きの一部です。
ですから、今日のレッスンを額面通りに受け取って肩透かしをくらわないようにしましょう。 無限が奇妙な振る舞いをするという事実に、あなたの心を揺さぶらせてください。 そして、より多くの理解、そして何よりもより多くの数学を切望するようにしましょう。
本日はお読みいただき、そして一緒に無限について考えていただきありがとうございました!
。
コメントを残す