Sum Of Product (SOP) & Product Of Sum (POS)

Product Of Sum (POS) & Sum Of Product (SOP)

Sum Of Product (SOP)

Sum of ProductとはSOPの省略形のことで、SOPの略です。 Sum of Product形式はブール代数における表現形式の一つで、入力の異なる積項を合計したものである。

SOPをよりよく理解するためには、最小項について知る必要がある。

最小項

最小項とは、最小数の入力の組み合わせに対して真となる項をいう。 ANDゲートも入力がすべて真のときのみ真を返すので、最小項は下表のように入力の組み合わせのANDであると言えます。 各組み合わせは小さなmで示される最小項を持ち、その10進数の組み合わせ番号が添え字で書かれる。 これらの最小項は、特定の入力の組み合わせでのみ真となる。

• You may also read: デジタル非同期カウンタ（リップルカウンタ） – 種類、動作 & アプリケーション

積和演算（SOP）形式の種類

積和演算の形式にはいくつかの種類があります。

• Canonical SOP Form
• Non-Canonical SOP Form
• Minimal SOP Form

Canonical SOP Form

これが標準のSum Of Productの形式です。 出力が真となる関数の最小項をOリングすることで形成される。 これはSum of Min termsまたはCanonical disjunctive normal form (CDNF)とも呼ばれる。 これは単なる洒落た名前である。 “canonical “は「標準的な」、”disjunctive “は「論理和」を意味します。

CanonicalSOP式は、和記号∑と出力が真となる中括弧内のmintermsによって表現されます。

例えば、関数の真理値表を以下に示す。

この関数について、正規のSOP式は

F = ∑( m1, m2, m3, m5 )

これは関数が最小項{1、2、3、5}に対して真であることを意味している。

総和を展開するとこうなる。

F = m1 + m2 + m3 + m5

ここでmin項を式に入れると

F = A̅B̅C + A̅BC̅ + AB̅C

定数形式はその積項で補完されるか非補充のすべての入力を含む＜6038>

こちらもお読みいただけます。 Digital Synchronous Counter – Types, Working & Applications

Non-Canonical SOP Form

このフォームは名前が示すように、SOP 式の非標準化されたフォームです。 積項はmin項ではありませんが、簡略化されています。 上の関数を正規形として例にとってみよう。

f = a̅b̅c + a̅bc̅ + ab̅c

f = a̅b̅c + a̅b(c̅ + c) + ab̅c

f = a̅b̅c + b̅b + a̅bc + a̅bc

f = ăb̅c + ăbc + ab̅c

f + a̅c A̅B(1) + AB̅C

F = A̅B̅C + A̅B + AB̅C

この式も積和形式のままだが、これは非積和形式であり、積和を表す。正規形または非標準化形。

Minimal SOP Form

この形式は、関数のSOP式を最も単純化したものです。 また、非正規形の一形態である。 最小SOP形式はブール代数の定理で作ることができるが、カルノーマップ（K-map）を用いると非常に簡単に作ることができる。

上で述べた関数をカノニカル形式で例にしてみましょう。

そのKマップは次のようになります。

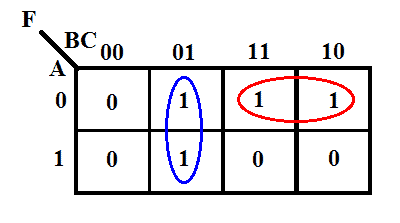
K-map によると、出力式は

F = B̅C + A̅B

これは当該関数に対して最も単純化&した最適式となります。 この式では、2入力ANDゲートが2つ、2入力ORゲートが1つで済みます。 しかし、正規形は 4 つの 3 入力 AND ゲート & 1 つの 4 入力 OR ゲートを必要とし、最小形の実装よりも比較的コストがかかります。

• You may also read: リングカウンタ & Johnson Counter – Construction & Operation

Sum Of Product (SOP) の回路図

SOP expression は2レベルの AND-OR デザインで、第1レベルのゲートは AND ゲート、第2レベルのゲートは OR ゲートを実装しています。 SOP式の回路図には、ANDゲートのグループアレイ & ORゲート1つが必要です。

どのSOP式も、下図に示すように、すべての入力はANDゲートを通過し、これらのANDゲートの出力はORゲートを通過するように設計されています。

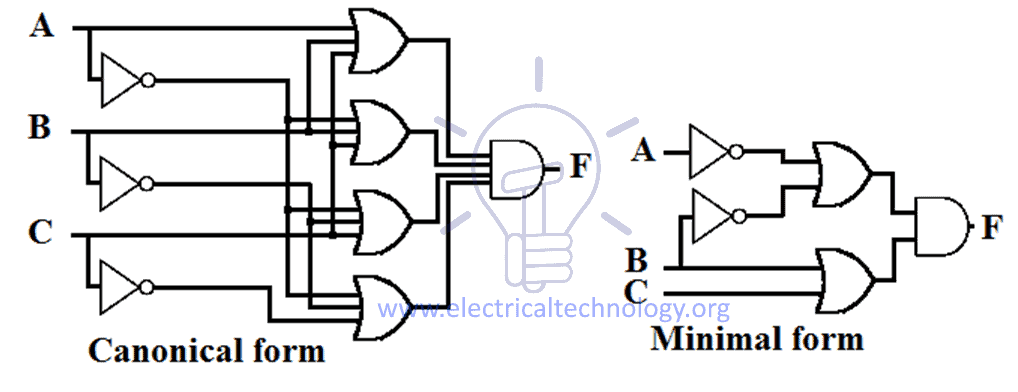
関数の正規表現と最小 SOP 式の設計例を次に示します。

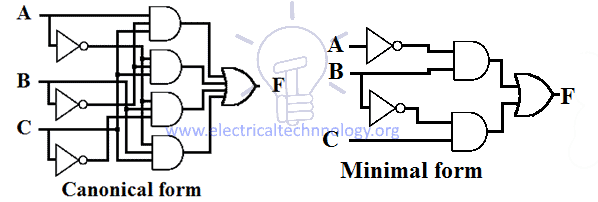
最小 SOP から正規表現への変換

最小または任意の種類の非正規表現から正規表現への変換は非常に簡単です。 そこで、最小SOPの各項を、入力の補完形と非補完形の和に乗じる。

最小SOP形式

F = A̅B + B̅C

項A̅Bには入力Cがないので、（C+C̅=1）なのでA̅Bに（C+C̅）を掛けることになる。 B̅Cの項には入力Aが欠けている。 となるので、(A+A̅)

F = A̅B(C + C̅) + B̅C(A + A̅)

F = A̅BC + A̅BC̅ + AB̅C + A̅B̅C

さてこの式は正規形になっていますね。

正準SOPから正準POSへの変換

標準SOP式は標準POS（和の積）式に変換することができる。 例えば、上の関数は正準SOP形式

F = A̅B̅C + A̅BC̅ + AB̅C

F = ∑ ( m1, m2, m3, m5 )

この関数の残りの項は出力を偽とした最大項である。 これらの最大項はM0,M4,M6,M7である。 これらの最大項はPOS式ではこれらの最大項の積として使用される。 積の記号は∏である。

F = ∏ ( M0, M4, M6, M7)

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

Max項はmintermsの補集合である。 つまり、M0=(A+B+C)となるわけです。

• You may also read: リップルキャリーとキャリーの先読み加算器

正規SOPから最小SOPへの変換

正規SOPは最小SOPに変換することができる。 カルノー写像やブール代数の定理を使って変換することができる。 K-map法は非常に簡単で、その例は上記の最小SOP形式で行われている。

最大項

最大項とは、入力の組み合わせの最大数に対して真、または入力の1つの組み合わせのみに対して偽となる項または式を意味します。

3つの入力変数の最大項を以下に示します。

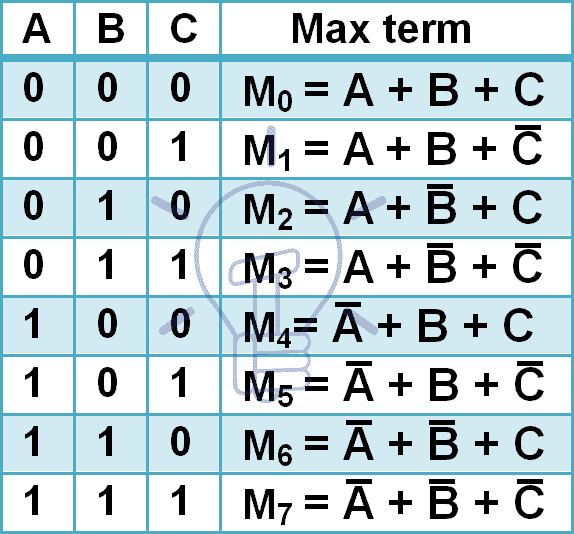
3つの入力は8通りの組み合わせを持つので、8つの最大項を持つことになります。 Maxtermは大文字のMで表し、添え字に10進数の組み合わせ番号を付けます。

Maxtermでは、前述の組み合わせが適用されたときのみMaxtermが’0’を与えるので各入力が補われ、Maxtermはmintermの補集合となります。

M3 = m̅3

M3 = (A̅BC)’

M3 = A + B̅ + C̅ DE Morganの法則

A=0 では最大項はA & A=1 では最大項は A̅で成り立つ理由です

以下の記事も参照してください。 デジタルフリップフロップ – SR、D、JK、Tフリップフロップ

積和演算の種類

積和演算には、さまざまな種類があります。

• Canonical POS Form
• Non – Canonical Form
• Minimal POS Form

Canonical POS Form

Product of Max term、Canonical conjunctive normal form (CCNF) とも呼ばれるものです。

この形式では、出力が偽となる最大公約数は一緒にANDされる。

正規品詞表現は、以下の例に示すように∏と括弧で出力が偽となる最大公約数で表現される。

F = ∏ (M0, M4, M6, M7)

積を展開する

F = M0.M4.M6.M6.M7

Max項を置く

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

正規形にはすべての入力がその各 Sum 項で補われるか非補われるかであり

• あなたはまたそれを読んでいるかもしれません。 555 タイマーを使用した拍手スイッチ回路電子プロジェクト

Non – Canonical Form

標準形式でない和表現の積を Non-Canonical Form と呼びます。

f = (a+b+c)(a̅+b+c)(a̅+b̅+c̅)

f = (b+c)(a̅+b̅+c)(a̅ +b̅+c̅)

f = (b+c)(a̅+b＋c＋a̅)

f = (a̅ +b̅ +c̅+b＋c＋a̅+c̅)(a̅ + b＋c̅)

同じだが反転した項は、2つのMax項を排除して1つの項を形成し、それを証明する例です。

= (a+b+c) (a̅+b+c)

= aa̅+ab+ac+a̅b+bb+bc+a̅c+bc+cc

= 0+ab+ac+a̅b+a̅c+b+bc+c

= a(b+c)+a = 0+ab+ac

=a(b+c)+b(1+c)+c

となる。

= (B+C)(A+A̅)+B(1)+C

= (B+C)(0)+B+C

= B+C

得られた式はまだ積和の形式ですが、非積和の形式であることがわかります。正準形式

最小 POS 形式

これは非正規の POS 式を最も単純化・最適化した形式です。 最小の和積形式は、上に挙げた非正規の例のようにブール代数の定理を使って実現できる。

最小のPOS形式は、その実装時に使用する入力と論理ゲートの数が少ないため、コンパクトで高速かつ低コストの実装のために正準形式よりも好まれている理由である。

上の関数を例にとると

関数のKマップ

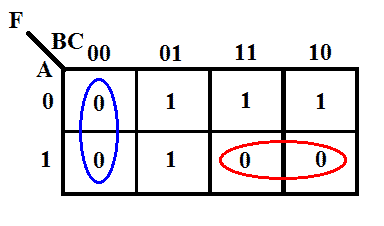
Kマップによる最小表現

F = (B+C) (A̅+B̅)

得られた表現は最小積和型である。 しかし、2入力のORゲート2個と2入力のANDゲート1個で済む。 しかし、正規形は3入力のORゲート4個と4入力のANDゲート1個が必要です。

• You may also read: 負帰還と負帰還増幅器システム

積和演算（POS）の回路図

積和演算はOR-ANDという特殊な回路図があります。 OR-ANDでは、入力は第1レベルのゲートであるORゲートのアレイを通過し、第1レベルのORゲートの出力は第2レベルのゲートであるANDゲートを通過します。

この設計で使用する入力数とゲート数は、実装する式によって異なります。 以下に、正規形と最小形のPOSの設計図を示す。

最小形POSから正規形POSへの変換

ご存知のように、POSの正規形は最大項を持ち、最大項には補完または非補完のすべての入力が含まれる。 そこで、すべての和項を補完された入力と補完されなかった入力の積で足すことにします。

最小POS形式

F = (A̅+B̅) (B+C)

(A̅+B̅) 項にはC入力がないので (CC̅) と追加する。 (B+C) 項は A 入力がないので、(AA̅) を追加します。

F = (A̅+B̅+CC̅) (B+C+AA̅)

F = (A̅+B̅+C)(A̅+B̅+C̅)(A+B+C)(A̅+B+C)

この式が正規形となりました

• こちらのページもどうぞ。 カウンタと電子カウンタの種類

正規形POSからSOPへの変換

Sum式の積は、正規形の場合のみSum of Product形式に変換することが可能です。 正規形POSと正規形SOPは相互変換可能であり、互いに変換することができます。 POSからSOPへの変換の例を以下に示す。

POSの正準形

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C)

正規形ではそれぞれの和項が最大項なのでこうも書き表せる。

F = ∏(M0,M4,M6,M7)

残りの入力の組み合わせは、その出力が真となる関数の最小項となる。 SOP式に変換するために、まず記号を和（∑）に変え、残りのmintermを使う。

F = ∑ (m1,m2,m3,m5)

ここで和の記号を展開して正規のSOP式とする。

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

Min項は同じ入力の組み合わせのMax項の補数。

Canonical to Minimal POS

canonical Product of Sum表現はカルノーマップ (K-map) によって Minimal Product of sum 形式に変換することができる。

K-mapの使用は非常に簡単であり、K-mapが好まれる理由である。 最小のPOS表現では、K-mapの0はグループにまとめられ、グループは0からできているので、得られる表現は補集合となる。

• Digital Logic NOT Gate – Digital Inverter Logic Gate
• Exclusive-NOR (XNOR) Digital Logic Gate
• Digital Logic NOR Gate
• Digital Logic NAND Gate

も合わせてお読みください。