2.12: Van der Waalsの式

van der Waalsによる式は、理想気体の方程式をわかりやすく拡張したものです。 Van der Waalsの式は

理想気体の式よりも実気体の圧力-体積-温度データによく適合する。 この改良された適合性は、各ガスについて実験的に決定されなければならない2つのパラメータ（” \(a)” と “b)” と指定）を導入することによって得られる。 ファンデルワールス方程式は、現実の気体と理想気体の違いをシンプルな物理的イメージで表現しているので、現実の気体の挙動を理解する上で特に有用である

ニュートンの法則からボイルの法則を導くとき、気体分子は互いに作用しないと仮定します。 単純な議論では、これは近似的にしか成り立たないことがわかる。 実際の気体分子は互いに作用し合っているはずである。 短い距離では互いに反発し合う。 ある程度長い距離では、互いに引き合う。 理想気体の式は、§10で述べた基本的な仮定から、統計熱力学の理論を応用して導くこともできる。 分子の性質について異なる仮定をすることで、統計熱力学を応用してファンデルワールス方程式を導出することができます。 必要な仮定は、分子が有限の体積を占め、分子間の距離の逆数乗として変化する力で互いに引き合うことである。 (引力は通常 \(r^{-6}) に比例すると仮定される)

実際の気体分子が互いに引き合い、反発し合うことを認識するには、どんな気体でもその温度を下げ、加える圧力を上げることで液化することができることを思い出せば十分であろう。 さらに冷やすと固体になります。 さて、固体の特徴は、形状を保つことと、ほとんど圧縮されないことの2点である。 固体が圧縮されないのは、構成する分子同士の反発力が重要で、分子同士が接近したためと考えられる。 固体を圧縮するためには、分子同士をさらに接近させなければならないので、大変な力が必要になる。 一方、氷を部屋の中に投げ入れると、氷を構成している水の分子はすべて一緒に部屋の中を飛んでいく。 これは、氷の分子が互いに引き合っているためで、そうでなければ、氷を投げれば、乾いた砂を投げるように、それぞれが別の道を歩むことになる。

気相では分子が離れているが、液相や固相では分子がまとまっている。 沸点では、液体の体積は凝縮した気体の体積よりはるかに小さい。 凝固点では、固体の体積は凍結した液体の体積とわずかに異なるだけで、0より大きいことは確かである。 このような当たり前のことは、どんな分子にも特徴的な体積があると仮定すれば、容易に説明できる。 このことは、分子間力の性質によるものと理解することができる。明らかに、分子間力は一対の分子間の距離が小さくなるほど強くなる。 液体や固体は一定の体積を占めるので、分子間距離が小さいときには、反発力の方が吸引力よりも急速に大きくならざるを得ない。 凝縮相のモル体積について話すと便利なことがよくある。 モル体積とは、純物質1モルの体積を意味する。 凝集相のモル体積は、分子間の引力と斥力が釣り合っている分子間距離によって決まる

明らかに、凝集相では分子が互いに非常に接近している。 分子間の空隙が無視できると仮定すると、凝縮相の体積は試料中の分子の数に分子1個の体積をかけたものにほぼ等しくなる。 そうすると、モル体積はアボガドロ数×1分子の占める体積となる。 密度Dとモル質量( \overline{M}) がわかれば、モル体積( \overline{V}) は

The volume occupied by a molecule.となり、次のように求められます。 V({}_{molecule}), becomes

Thomas

ファンデルワールスの式に現れる圧力と体積は、実際の気体の圧力と体積である。 van der Waalsの方程式の項を理想気体の方程式と関連づけることができる。 ⒶとⒷは、仮想的な理想気体の圧力と体積と考えるのが便利です。 That is

That is &=nRT \end{align*}]

That is

分子が相互作用しない点質量のモデルから理想気体の方程式を導出する。 つまり理想気体の体積は、個々の分子の体積がゼロである気体が占める体積である。 現実の気体の個々の分子が実効的に占める体積は \({b}/{overline{N}}) moles of them effectively occupy a volume

Fan der Waalsの式では、現実の気体の体積は非相互作用点質量が占める体積である \(V_{idealpha gas}) に気体分子自身の実効体積を足したものであるとする。 (実際の気体分子のデータをファンデルワールス方程式に当てはめると、通常、液体の密度と分子量から推定される体積よりも、 \(b) の値はいくらか大きくなる。 問題24参照）

同様に、

となるが、これは実際の気体の分子間の引力相互作用の論理的帰結として理解することができる。 となり、実気体の圧力は仮想的な理想気体の圧力よりも({left({n}/{V}right)}^2})に比例した分だけ小さいことがわかる。 このときの比例定数は “à “である。 Δ({n}/{V})は気体分子のモル密度(単位体積あたりのモル数)ですから、濃度の指標となります。 同じ種類の分子同士の衝突回数は、濃度の二乗に比例する。 (この点については4,5章で詳しく述べます。)したがって、 \({left({n}/{V}}right)}^2} は実際の気体分子同士が接近する頻度を示す指標となります。 近づいたときに互いに引き合うとすれば、その効果は◇（◇left({n}/{V}right)}^2◇に比例するはずである。 つまりファンデルワールスの方程式は、実際の気体の圧力は、魅力的な相互作用の頻度と強さに比例した量だけ、仮想的な理想気体の圧力と異なるという考えと一致する。

しかし、なぜ魅力的な相互作用がこのような効果を持つべきなのか、なぜ実際の気体の圧力は、仮想的な理想気体の圧力より低くなければならないのか。 おそらく定性的なイメージを描くには、魅力的な分子間力が気体分子を凝集させる傾向があることを認識するのが最もよい方法であろう。 結局、低温で分子を液体に凝集させるのは、この引力なのである。 沸点以上では、気体分子は別々の道を歩むことができるため、この傾向の影響は限定的である。しかし、気体の中でも、分子が占める体積を小さくする傾向のある引力が作用するはずである。 気体が占める体積は気体自体の特性ではなく、容器の大きさによって決まるので、この凝集傾向は圧力の低下として表現される

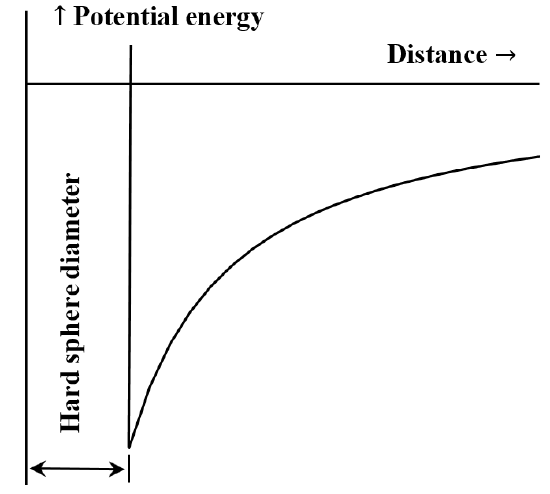
粒子や化学物質間の相互作用をポテンシャルエネルギー対距離図で説明することは、しばしば有用である。 ファンデルワールス方程式は、分子が接触するまで、分子間の反発的な相互作用が存在しない場合に対応する。 一旦接触すると、さらに近づけるために必要なエネルギーは恣意的に大きくなる。 これを「硬い球体」のように振る舞う、と表現することが多い。 2つの分子間の引力は、距離が長くなるにつれて小さくなる。 距離が非常に離れている場合、引力の相互作用は非常に小さくなる。 分子が無限に離れているとき、相互作用のエネルギーはゼロであると言う。 最初に大きく離れた2つの分子が静止しており、互いに引きつけあっているとすると、分子は運動エネルギーを得ながら自然に互いに向かって移動する。 ポテンシャルエネルギーは近づくと減少し、分子が接触したときに最小となる。 したがって、ファンデルワールスの方程式は、図5のような距離に対する位置エネルギーのグラフを意味する。