関数とマッピング

さて、関数とマッピングでは、関数とマッピングという特殊な関係の学習をしていきます。 それを理解するために、いくつかの実例を挙げてみよう。

これらの質問にはすべて
固有の答えがあります。 これをラーニングマッピングでどのように関連付けることができるかを
見てみましょう。

● 太陽はどこから昇るか？

東

● インドの首都はどこでしょうか？

デリー

● 4の後継は？

5

●5 と 3 の和は？

8

写像または関数：

AとBが空でない二つの集合であるとき、集合Aから集合Bへの関係 ‘f’ は、集合Aのすべての要素が集合Bの固有の要素と関連している場合、

● AからBへの関数 ‘f’ は f : A → B で表される。

●fをAからBへの関数とし、x∈Aとすると、f（x）∈Bここでf（x）はfの下でのxの像、xはf（x）の「f」の下での前像と呼ばれる。

注意：

fがAからBへの写像であるためには、

●Aのすべての要素はBに像を持たねばならない。

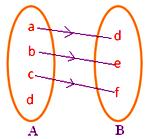
● Aの要素は2つ以上のイメージを持ってはならない。

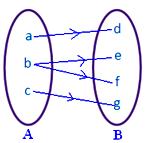
● Aの異なる要素がBにおいて同じイメージを持つことは可能である。

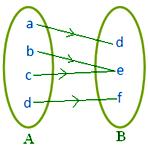
注意：

すべてのマッピングは関係だが、すべての関係はマッピングでない可能性がある。

関係の特殊な種類としての関数：

ここで関係の特殊な種類としての関数を思い出して復習しよう。 AとBが空でない二つの集合だとすると、Aのそれぞれの要素とBの固有の要素を関連付ける規則 ‘f’ は関数またはAからBへのマッピングと呼ばれている。
f ‘がAからBへの写像である場合、

f: A → B

と表現し、’f ‘がAからBへの関数であると読む。
f ‘がAからBへの関数で x∈A と y∈B なら、y は関数 ‘f ‘におけるx要素の像と言い、 f(x) で表記される。
したがって、y = f(x)

ここで、要素xをyの前像と呼ぶ。

したがって、AからBへの関数に対して
● AとBは空でないことが望ましい。

●Aの各要素はBにイメージを持つべきである。

●Aのどの要素もBに複数のイメージを持つべきではない。

●Aの2つ以上の要素がBに同じイメージを持つこともある。

●f : x → yとは、AからBへのfの関数において、Aの要素xがBにイメージyを持つことをいう。

● すべてのfイメージがB内にある必要はないが、B内にAのどの要素に対してもfイメージではない要素があってもよい。

●関係と写像

順序対

二つの集合のデカルト積

関係

関係の領域と範囲

関数か写像

領域 Co->

関係

関数と写像

領域 Co-> 関係(ref)の領域(a)と範囲(b)。関数の領域と範囲

●関係性とマッピング-… ワークシート

数学関係ワークシート

関数またはマッピングに関するワークシート

中学1年算数問題

中学1年算数練習
関数またはマッピングから HOME PAGE