心理学研究法

相関研究とは何か？

相関研究は、研究者が二つの変数（二値または連続）を測定し、統計的関係（すなわち。 相関研究とは、非実験型研究の一種で、研究者が2つの変数（二値または連続）を測定し、無関係な変数をほとんどあるいはまったく制御せずに、それらの間の統計的関係（すなわち相関）を評価するものです。 変数間の統計的関係に関心のある研究者が、実験ではなく、相関研究を行うことを選択する理由はたくさんある。 第一は、統計的関係が因果関係であると信じていない、あるいは因果関係に関心がないことである。 科学の2つの目標は、記述することと予測することであり、相関研究戦略によって研究者はこれら2つの目標を達成することができることを思い出してください。 具体的には、この戦略は、2つの変数の間の関係の強さと方向を記述するために使用することができ、変数の間に関係がある場合、研究者は一方の変数のスコアを使用して、他方のスコアを予測することができます（本章の複雑な相関のセクションでさらに説明する回帰という統計技法を使用します）。

研究者が実験ではなく、相関研究を選択するもうひとつの理由は、関心のある統計的関係は因果関係があると考えられるが、研究者が独立変数を操作することが不可能、非実際的、または非倫理的であるため、操作できない場合です。 例えば、ある研究者が大麻の使用頻度と記憶能力の関係に興味を持ったとしても、倫理的に大麻の使用頻度を操作することができません。 そのため、相関研究戦略に頼らざるを得ません。彼らは単に、人々が大麻を使用する頻度を測定し、記憶の標準化テストを使用して彼らの記憶能力を測定し、そして人々が大麻を使用する頻度が記憶テストのパフォーマンスと統計的に関連しているかどうかを決定しなければなりません。

相関は、測定値の信頼性と妥当性を確立するためにも使用されます。 たとえば、ある研究者は、短い外向性テストを、すでに有効であることが示されている長い外向性テストとともに、多数の参加者に実施することによって、その有効性を評価することができます。 そして、参加者の短いテストの得点が、長いテストの得点と強く相関しているかどうかを確認することができます。 どちらのテストの得点も他方を引き起こすとは考えられないので、操作する独立変数がありません。 実際、この種の研究には、独立変数や従属変数という言葉は当てはまりません。

相関研究のもうひとつの強みは、実験研究よりも外部妥当性が高いことが多いということです。 内部妥当性と外部妥当性の間には通常トレードオフがあることを思い出してください。 実験に大きな制御を加えれば、内的妥当性は高まるが、現実には存在しない人工的な条件が導入されるため、外的妥当性が犠牲になることが多い。 一方、相関研究は、何も操作・制御されていないため、一般的に内的妥当性は低いが、外的妥当性が高い場合が多い。

最後に、この内的妥当性と外的妥当性のトレードオフを発展させ、相関研究は理論に対する収束的な証拠を提供するのに役立つことがある。 もしある理論が、内的妥当性の高い実験と外的妥当性の高い相関研究によってサポートされていれば、研究者はその理論の妥当性にもっと自信を持つことができる。 具体的な例としては、暴力的なテレビを見ることと攻撃的な行動の間に関係があることを証明する相関研究が、その関係が因果関係であることを確認する実験研究によって補完されている（ブッシュマン & ヒューズマン、2001年）。

相関研究には必ず量的変数が必要？

研究者の初心者によくある誤解は、相関研究には、2つの外転テストのスコアや人々が経験した日々の煩わしさと症状の数など、2つの量的変数が必要だということです。 しかし、相関研究の特徴は、2つの変数を測定することであり、どちらかを操作することではありません。 例えば、ある研究者がローゼンバーグ自尊心尺度をアメリカの大学生50名と日本の大学生50名に実施したとします。 これは被験者間実験のように「感じ」ますが、研究者は学生の国籍を操作していないので、これは相関研究なのです。 また、カシオッポとペティによる大学教員と工場労働者の認知欲求を比較した研究も同様である。

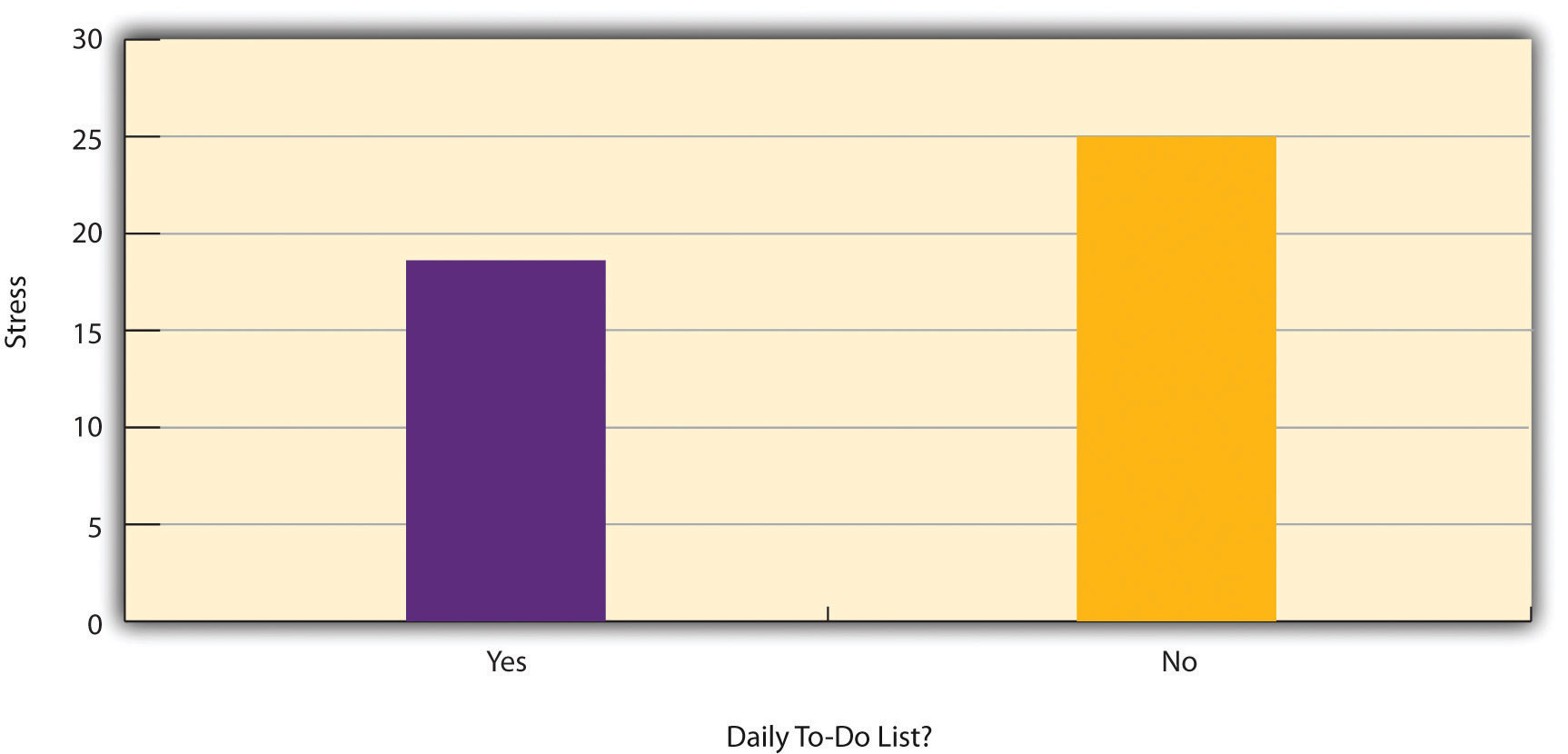
図6.2は、毎日やることリスト（ToDoリスト）を作っているかどうかとストレスの関係についての仮説的研究のデータである。 独立変数が操作されたかどうかが不明なため、これが実験なのか相関研究なのかが不明なことに注意してください。 もし研究者が、ある参加者には毎日のToDoリストを作るように、他の参加者には作らないようにランダムに割り当てたのであれば、それは実験となります。 もし、研究者が参加者に毎日のToDoリストを作っているかどうかを尋ねただけなら、それは相関研究です。 この違いが重要なのは、もしこの研究が実験であれば、毎日のToDoリストを作成することで参加者のストレスが減少したと結論づけることができるからです。 しかし、相関研究であれば、これらの変数が統計的に関連しているとしか結論づけられないのです。 おそらく、ストレスを感じることは、人の計画性にマイナスの影響を与えるのでしょう（方向性の問題）。 あるいは、良心的な人ほどToDoリストを作りやすく、ストレスを感じにくいのかもしれません（第3変数問題）。 重要なのは、ある研究が実験的か相関的かを定義するのは、研究されている変数でも、変数が定量的かカテゴリー的かでも、データを分析するために使われるグラフや統計の種類でもない、ということです。

相関研究におけるデータ収集

繰り返すが、相関研究の特徴は、どちらの変数も操作されていないことである。 変数をどのように、あるいはどこで測定するかは問題ではありません。 研究者は、参加者に実験室に来てもらって、コンピュータによる逆数スパン課題とコンピュータによる危険な意思決定課題をやってもらい、その後、2つの課題の参加者の得点の関係を評価することができる。 あるいは、ショッピングモールに行き、環境に対する考え方や買い物習慣を聞き、この2つの変数の関係を評価することもできます。 これらの研究は、独立変数が操作されていないため、どちらも相関的な研究となります。

量的変数間の相関

量的変数間の相関は、散布図を用いて示されることが多い。 図6.3は、人が受けるストレスの量と身体症状の数との関係についての仮想的なデータを示しています。 散布図の各点は、両変数の1人分のスコアを表しています。 例えば、図6.3の丸で囲んだ点は、ストレスのスコアが10で、身体的症状が3つある人を表している。 すべての点を考慮すると、ストレスが多い人ほど身体症状も多い傾向があることがわかる。 これは、ある変数のスコアが高いほど、他の変数のスコアも高くなる傾向があるという、正の関係の良い例である。 言い換えれば、それらは同じ方向に動き、両方が上がるか下がるかのどちらかです。 負の関係は、一方の変数のスコアが高いと、他方のスコアが低くなる傾向があるものである。 言い換えれば、それらは反対方向に動く。 たとえば、ストレスが高いと免疫系機能が低下するため、ストレスと免疫系機能の間には負の関係があります。

量的変数間の相関の強さは、通常、ピアソンの相関係数(またはピアソンのr)という統計量を使用して測定されます。 図6.4が示すように、ピアソンのrは-1.00（最も強い負の関係）から+1.00（最も強い正の関係）までの範囲です。 0の値は、2つの変数の間に関係がないことを意味する。 ピアソンのrが0のとき、散布図上の点は形のない “雲 “を形成します。 その値が-1.00または+1.00に向かうにつれて、ポイントは1本の直線上に落ちるように近づきます。 相関係数が±.10に近いものは小、±.30に近いものは中、±.50に近いものは大とされる。 ピアソンのrの符号は、その強さとは無関係であることに注意してください。 例えば、ピアソンのrの値が+.30と-.30であれば、同じ強さであり、一方が中程度の正の関係を表し、他方が中程度の負の関係を表しているだけである。 信頼性係数を除けば、心理学で見られる相関関係のほとんどは、小さいか中程度の大きさである。 Kristoffer Magnussonが作成したウェブサイトhttp://rpsychologist.com/d3/correlation/は、相関の優れたインタラクティブな視覚化を提供しており、散布図に対応する変化を見ながら、相関の強さと方向を調整することができます

Pearson の r の値が誤解を招く可能性がある、よくある状況が 2つあります。 Pearsonのrは、ポイントが直線で最もよく近似される直線的な関係に対してのみ良い指標となります。 曲線で近似されるような非線形の関係には適していません。 例えば、図6.5は、人々の一晩の睡眠時間とうつ病のレベルとの間の仮想的な関係を示している。 この例では、睡眠時間が約8時間の人が最も抑うつ度が低い傾向があるため、点を最もよく近似する線は曲線、つまり逆さ「U」の字になる。 睡眠時間が短すぎる人、長すぎる人は、より落ち込む傾向がある。 図6.5は、うつ病と睡眠にかなり強い関係があることを示しているが、散布図の点が一本の直線にうまく当てはまらないため、ピアソンのrはゼロに近くなる。 つまり、ピアソンのrを使う前に、散布図を作って関係がほぼ直線であることを確認することが重要です。非線形関係は心理学ではかなり一般的ですが、その強さを測ることは本書の範囲外です。

ピアソンのrの値が誤解を招く可能性がある他の一般的な状況は、変数の一方または両方が、集団と比較してサンプルの範囲が限られている場合である。 この問題は、範囲の制限と呼ばれる。 例えば、図6.6の散布図で示されるように、人々の年齢とヒップホップ音楽の楽しみの間に強い負の相関があると仮定します。 ここでのピアソンのrは-.77である。 しかし、図6.6の斜線で示した18歳から24歳の人たちだけのデータを集めると、この関係はかなり弱くなるように思われる。 したがって、範囲を限定しないような研究計画を立てることが望ましい。 例えば、年齢が主要な変数の一つであれば、幅広い年齢層からデータを収集するように計画することができます。 しかし、範囲の限定は常に予測できるものでも、簡単に回避できるものでもないので、範囲の限定の可能性がないかデータを調べ、それを踏まえてピアソンのrを解釈することは良い方法です。 (

Correlation Does Not Imply Causation

“相関は因果関係を意味しない “という言葉を繰り返し聞いたことがあるかも知れませんね。 面白い例として、ある国の 1 人当たりのチョコレート消費量と、その国の国民に与えられるノーベル賞の数の間に正の相関 (Pearson’s r = 0.79) があることを示した、2012 年の研究が挙げられます。 しかし、これはチョコレートを食べることでノーベル賞を受賞することを意味しないことは明らかであり、親が子供にもっとチョコレートを食べさせることを推奨して、ノーベル賞の受賞数を増やそうとしても意味がないだろう。 1つ目は、「方向性の問題」と呼ばれるものである。 たとえば、運動するかどうかが、どれくらい幸せか（運動しない人よりも運動する人のほうが平均的に幸せか）と統計的に関係があることを示す研究があるとします。 この統計的関係は、運動が幸福を引き起こすという考えと矛盾しないが、幸福が運動を引き起こすという考えとも矛盾しない。 幸せだと元気が出るのか、ジムに通うなどして人との交流の機会を求めるようになるのでしょう。 相関関係が因果関係を意味しない2つ目の理由は、「第3変数問題」と呼ばれるものです。 例えば、ノーベル賞を多く受賞した国ほどチョコレートの消費量が多いという事実は、ヨーロッパの国々は世界の他の多くの国々と比べて、一人当たりのチョコレート消費量が多く、教育や技術への投資（これも一人当たりですが）が多いという地理的条件を反映しているのでしょう。 同様に、運動と幸福の統計的関係は、身体の健康など、第3の変数が他の2つを引き起こすことを意味する可能性があります。 身体的に健康であることが、人々に運動をさせ、人々をより幸福にするのかもしれない。

偽相関の優れた面白い例はhttp://www.tylervigen.comで見ることができます（図6.7はそのような例です）。 出典 http://tylervigen.com/spurious-correlations (CC-BY 4.0)