円の円周 – 解説と例題

多角形の外周の求め方を前に見てきました。 円は多角形でないことが分かっているので、円周はないはずです。 今回は、円の円周の求め方、円の円周の公式、円の円周に関する例題について説明します。

円の円周とは

正方形や長方形などの多角形の周りの距離を外周（P）と呼びます。 一方、円の周りの距離を円周(C)といいます。

Why do we do need to calculate the circumference of a circle?

Finding the circumference of an object is important in the following scenarios:

Whether you want buy a bra, trouser or sweater, you need to know the distance around your waist or chest. あなたの体は完全な円ではありませんが、巻き尺を使ってその周囲を測定する必要があります。 仕立屋は主にdress.

の円周を決定するためにこの技術を使用します。また、工芸品を作る、ホットタブ周りにフェンスを置く、または単に学校のための数学の問題を解く円周を知る必要があります。

円の円周を見つける方法？

前に述べたように、円の周囲や周は、円または任意の円形状の周りの距離です。 円の円周は、円を作るために折ったり曲げたりした直線の長さと同じです。 円周はメートル、キロメートル、ヤード、インチなどで測られる。

円の周囲や円周を求めるには2つの方法がある。 最初の式は半径を使うもので、2番目は円の直径を使うものである。 ここで重要なのは、この2つの方法はどちらも同じ結果になるということです。

それでは見てみましょう。

円の円周は次式で与えられます。

C = 2 * π* R = 2πR

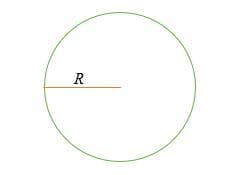ここで、

C = 円周または周囲、

R = 円の半径、です。

π = πとして知られる数学定数

または

C = π* D = π D

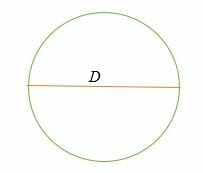
ここで、D = 2R =円の直径

どの円についても、その周りと直径の比率はπとして知られる定数と同じである。

円周/直径=π

C /D=π または C/2R=π

πの近似値（π）=22/7=3.1415926535897・・・・・・・。 (終端でない値)

円の円周の計算を簡単にするために、πの値を3.14とします(π=3.14)

円周の概念を磨くために以下のいくつかの例を見てみましょう。

例題1

半径8cmの円の円周を求める。

解答

円周=2 * π* R = 2πR

= 2 * 3.14 * 8

= 50.24cm とする。

例2

直径70mmの円の円周を計算する

解

円周 = π* D = π D

= 3.14 * 70

= 219.8 mm

例題3

半径10mの円形の花畑の周囲を計算せよ。

解答

円周=2 * π* R = 2πR

= 2 * 3.14 * 10

= 62.8 m.

例4

円の周囲は440ヤードである。 円の直径と半径を求めよ。

解答

円周 = 2 * π * R = 2πR

440 = 2 * 3.14 * R

440 = 6.8メートル。28R

両辺を6.28で割ると

R = 70.06

したがって、円の半径は70.06ヤードになります。 しかし、直径は円の半径の2倍なので、直径は140.12ヤードになる。

例題5

自転車の車輪の直径は100cmである。 157メートルの距離を移動するために、それぞれの車輪は何回転するか

解答

自転車の車輪の円周を計算する。

円周 = π D

= 3.14 * 100

= 314 cm

車輪の回転数を求めるには、かかった距離を車輪の円周で割ります。

157mをcmに変換してから割る必要があるので、157に100をかけて15700cmとします。 したがって、

回転数＝15700cm÷314cm

＝50回転です。

例題6

縦100cm、横50cmの長方形の針金を切り、折って円にする。 できた円の円周と半径を計算しなさい。

解答

できた円の円周＝長方形の針金の外周とする。

長方形の周囲＝2（L＋W）

＝2（100＋50）cm

＝2×150cm

＝300cm よって、円の円周は300cmとなる

次に半径を計算してください。

円周 = 2 π R

300 cm = 2 * π * R

300 cm = 2 * 3.14 * R300 cm = 6.28R

両辺を 6.28 で割る R = 47.0.77cm

ですから、円の半径は47.77cmになります。

例題7

バイクの各輪の半径は0.85mですが、各輪が1000回転したらバイクはどこまで動くか？

解答

まず、車輪の円周を求める。

円周 = 2 π R

= 2 * 3.14 * 0.85

= 5.338 m

移動距離は車輪円周に回転数をかけて求めよ。

Distance = 5.338 * 1000

= 5338 m

したがって、移動距離は5.338 kmに相当します。

練習問題

1. マイクとその友達に12インチピザが出されました。 マイクはその円周を計算することに興味があるようです。 彼を助けてあげてください！
2. ある正方形の周囲は、ある円の面積の1/3である。 正方形の長さをL単位とすると、円の直径をL単位で求めなさい。

答え

1. 12L/π インチまたは 37.67 インチ

前のレッスン｜メインページ｜次のレッスン

へ