Articles

Somma del prodotto (SOP) e prodotto della somma (POS)

Il Novembre 10, 2021 da admin

Prodotto della somma (POS) & Somma del prodotto (SOP)

Somma del prodotto (SOP)

Somma del prodotto è la forma abbreviata di SOP. Somma del prodotto è una forma di espressione in algebra booleana in cui diversi termini di prodotto degli input vengono sommati insieme. Questo prodotto non è una moltiplicazione aritmetica ma è un AND logico booleano e la Somma è un OR logico booleano.

Per capire meglio il SOP, dobbiamo conoscere il termine min.

Termine Min

Minterm significa il termine che è vero per un numero minimo di combinazioni di input. Questo è vero solo per una combinazione di ingressi.

Siccome anche la porta AND dà Vero solo quando tutti i suoi ingressi sono veri, possiamo dire che i termini min sono AND di combinazioni di ingressi come nella tabella qui sotto.

3 ingressi hanno 8 combinazioni diverse. Ogni combinazione ha un termine minimo denotato dalla piccola m e il suo numero di combinazione decimale scritto in pedice. Ognuno di questi mintermini sarà vero solo per la specifica combinazione di ingressi.

• Si può anche leggere: Contatore digitale asincrono (Contatore a ondulazione) – Tipi, funzionamento & Applicazione

Tipi di forme di Somma del prodotto (SOP)

Ci sono alcune forme diverse di Somma del prodotto.

• Forma SOP canonica
• Forma SOP non canonica
• Forma SOP minima

Forma SOP canonica

Questa è la forma standard di Somma del Prodotto. È formata da O Ring i mintermi della funzione per cui l’uscita è vera. Questo è anche conosciuto come Somma di Min termini o Forma normale disgiuntiva canonica (CDNF). È solo un nome di fantasia. “canonico” significa “standardizzato” e “disgiuntivo” significa “unione logica OR”.

L’espressione SOP canonica è rappresentata dal segno di somma ∑ e dai mintermini tra le parentesi per i quali l’output è vero.

Per esempio, la tabella di verità di una funzione è data qui sotto.

Per questa funzione l’espressione SOP canonica è

F = ∑( m1, m2, m3, m5 )

Che significa che la funzione è vera per i termini min {1, 2, 3, 5}.

Espandendo la sommatoria otteniamo.

F = m1 + m2 + m3 + m5

Ora mettendo i termini min nell’espressione

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

La forma canonica contiene tutti gli ingressi sia complementari che non complementari nei suoi termini prodotti.

Si può anche leggere: Contatore sincrono digitale – Tipi, funzionamento & Applicazioni

Forma non canonica SOP

Come suggerisce il nome, questa forma è la forma non standardizzata delle espressioni SOP. I termini del prodotto non sono i termini min, ma sono semplificati. Prendiamo la funzione di cui sopra in forma canonica come esempio.

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

F = A̅B̅C + A̅B(C̅ + C) + AB̅C

F = A̅B̅C + A̅B(1) + AB̅C

F = A̅B̅C + A̅B + AB̅C

Questa espressione è ancora in forma di Somma del Prodotto ma è nonforma canonica o non standardizzata.

Forma SOP minima

Questa forma è l’espressione SOP più semplificata di una funzione. È anche una forma non canonica. La forma SOP minima può essere fatta usando i teoremi dell’algebra booleana, ma è molto facile farla usando la mappa di Karnaugh (K-map).

La forma SOP minima è preferita perché usa il numero minimo di porte e linee di ingresso. è commercialmente vantaggiosa per le sue dimensioni compatte, la velocità veloce e il basso costo di fabbricazione.

Prendiamo un esempio della funzione data sopra in forma canonica.

La sua mappa K è data qui sotto.

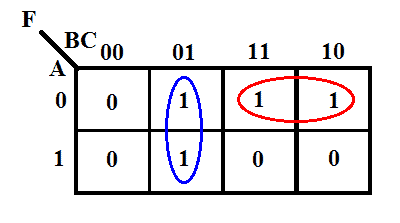
Secondo la K-map, l’espressione di uscita sarà

F = B̅C + A̅B

Questa è l’espressione ottimizzata più semplificata &per la funzione detta. Questa espressione richiede solo due porte AND a 2 ingressi &una porta OR a 2 ingressi. Tuttavia, la forma canonica ha bisogno di quattro porte AND a 3 ingressi &una porta OR a 4 ingressi, che è relativamente più costosa dell’implementazione della forma minima.

• Si può anche leggere: Contatore ad anello & Contatore Johnson – Costruzione & Funzionamento

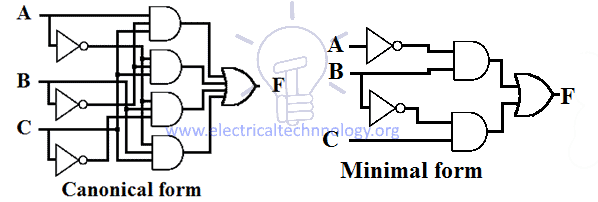
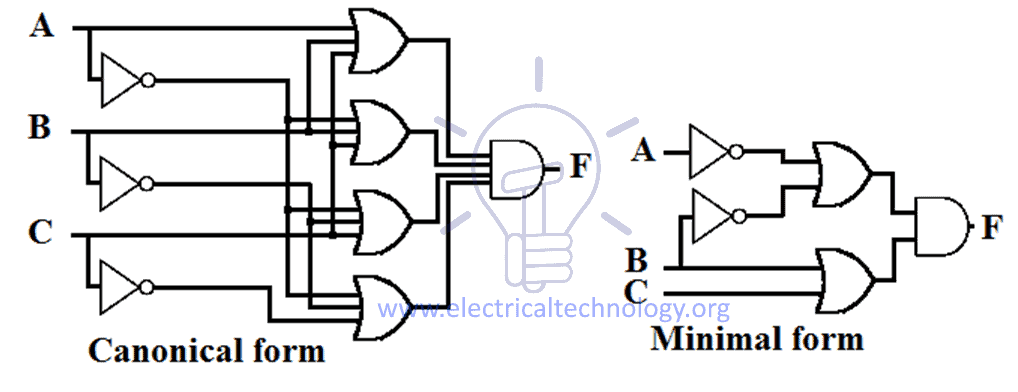
Progettazione schematica della Somma del Prodotto (SOP)

L’espressione SOP implementa un progetto a 2 livelli AND-OR in cui il gate di 1° livello è AND gate che segue il gate di 2° livello che è OR gate. La progettazione schematica dell’espressione SOP ha bisogno di un gruppo di porte AND &una porta OR.

Ogni espressione SOP ha un po’ la stessa progettazione, cioè tutti gli ingressi passano attraverso una porta AND e poi l’uscita di queste porte AND passa attraverso una porta OR come mostrato nella figura qui sotto.

Il numero di ingressi e il numero di porte AND dipende dall’espressione che si sta implementando.

Esempio di progetti di espressione SOP canonica e minima per una funzione è dato qui sotto.

Conversione da SOP minima a forma SOP canonica

La conversione da forma minima o qualsiasi tipo di forma non canonica a forma canonica è molto semplice.

Come sappiamo la forma canonica ha termini minimi &i termini minimi consistono di tutti gli ingressi sia completati che non completati. Quindi moltiplicheremo ogni termine del SOP minimo con la somma della forma complementare e non complementare dell’input mancante. Esempio di conversione per la funzione sopra in forma SOP minima è dato qui sotto.

F forma SOP minima

F = A̅B + B̅C

Il termine A̅B è l’ingresso mancante C. Quindi moltiplicheremo A̅B con (C+C̅) perché (C+C̅ = 1). Il termine B̅C manca dell’ingresso A. quindi sarà moltiplicato con (A+A̅)

F = A̅B(C + C̅) + B̅C(A + A̅)

F = A̅BC + A̅BC̅ + AB̅C + A̅B̅C

Ora, questa espressione è in forma canonica.

Conversione da SOP canonico a POS canonico

L’espressione SOP standard può essere convertita in un’espressione POS (prodotto di somma) standard. Per esempio, la funzione data sopra è in forma canonica SOP

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

F = ∑ ( m1, m2, m3, m5 )

I termini rimanenti di questa funzione sono termini max per cui l’output è falso. Questi termini max sono M0,M4,M6,M7. Questi termini Max saranno usati nell’espressione POS come il prodotto di questi termini max. Il simbolo del prodotto è ∏.

F = ∏ ( M0, M4, M6, M7)

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C)(A̅+B̅+C̅)

I termini Max sono il complemento dei termini minimi. Ecco perché M0=(A+B+C).

• Potresti anche leggere: Ripple Carry And Carry Look Ahead Adder

Conversione da Canonical SOP a Minimal SOP

Canonical SOP può essere convertito in minimal SOP. Può essere convertito usando la mappa di Karnaugh o i teoremi algebrici booleani. Il metodo K-map è molto facile e il suo esempio è stato fatto sopra nella forma SOP minima.

Prodotto di Somma

Prodotto di Somma abbreviato per POS.

Il prodotto di Somma è una forma in cui vengono presi i prodotti di diversi termini di somma degli input. Questi non sono prodotto e somma aritmetici ma sono rispettivamente AND e OR logici booleani.

Per capire meglio il Prodotto di Somma, dobbiamo conoscere il termine Max.

Termine Max

Maxterm significa il termine o l’espressione che è vero per un numero massimo di combinazioni di input o che è falso per una sola combinazione di input.

Siccome anche la porta OR dà falso per una sola combinazione di input. Quindi Maxterm è OR di ingressi complementari o non complementari.

I termini massimi per 3 variabili di ingresso sono dati qui sotto.

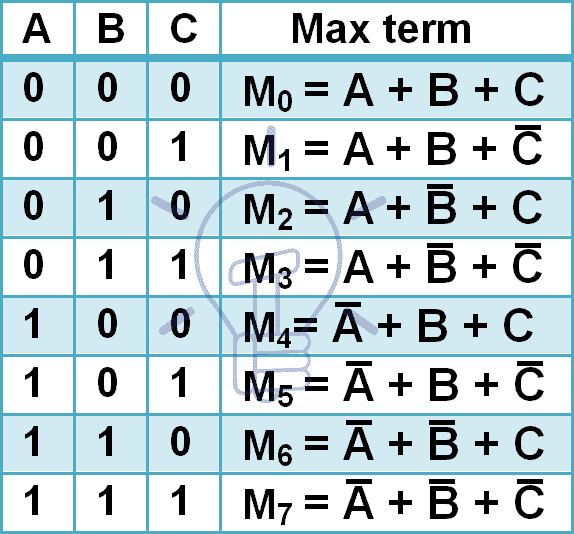
3 ingressi hanno 8 combinazioni diverse quindi avrà 8 maxtermi. I maxtermi sono indicati con la M maiuscola e il numero di combinazione decimale nel pedice come mostrato nella tabella data sopra.

Nel maxterm, ogni input è complementato perché Maxterm dà ‘0’ solo quando la combinazione menzionata è applicata e Maxterm è il complemento del minterm.

M3 = m̅3

M3 = (A̅BC)’

M3 = A + B̅ +C̅ DE legge di Morgan

Così è perché per A=0 Max termine consiste A & per A=1 Max termine consiste A̅.

Si può anche leggere: Flip-Flop digitali – SR, D, JK e T Flip Flops

Tipi di prodotto di forme somma

Ci sono diversi tipi di prodotto di forme somma.

• Forma canonica POS
• Forma non canonica
• Forma POS minima

Forma canonica POS

È anche conosciuta come Prodotto di termine Max o Forma normale congiuntiva canonica (CCNF). Canonical significa standard e conjunctive significa intersezione.

In questa forma, i Maxterms sono AND insieme per i quali l’output è falso.

L’espressione POS canonica è rappresentata da ∏ e i Maxterms per i quali l’output è falso tra parentesi come mostrato nell’esempio sotto riportato.

F = ∏ (M0, M4, M6, M7)

Espansione del prodotto

F = M0.M4.M6.M7

Mettendo i termini Max

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

La forma canonica contiene tutti gli ingressi sia complementati che non complementati in ogni suo termine di somma.

• Potresti anche leggere: Clap Switch Circuit Electronic Project Using 555 Timer

Forma non canonica

Il prodotto dell’espressione somma che non è in forma standard è chiamato forma non canonica.

Prendiamo la funzione sopra data come esempio.

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

F = (B+C) (A̅+B̅+C)(A̅+B̅+C̅)

Lo stesso ma i termini invertiti si eliminano da due termini Max e formano un solo termine per dimostrarlo ecco un esempio.

= (A+B+C) (A̅+B+C)

= AA̅+AB+AC+A̅B+BB+BC+A̅C+BC+CC

= 0+AB+AC+A̅B+A̅C+B+BC+C

= A(B+C)+A̅(B+C)+B(1+C)+C

= (B+C)(A+A̅)+B(1)+C

= (B+C)(0)+B+C

= B+C

L’espressione ottenuta è ancora in forma di prodotto di somma ma non èforma canonica.

Forma POS minima

Questa è la forma più semplificata e ottimizzata di un’espressione POS che non è canonica. Il prodotto minimo della forma Sum può essere ottenuto usando teoremi algebrici booleani come nell’esempio non canonico dato sopra. Un altro metodo per ottenere la forma POS minima è l’uso della mappa di Karnaugh, che è relativamente più facile dell’uso dei teoremi algebrici booleani.

La forma POS minima usa meno input e porte logiche durante la sua implementazione, ecco perché è preferita alla forma canonica per la sua implementazione compatta, veloce e a basso costo.

Prendiamo la funzione sopra data come esempio

K-map della funzione

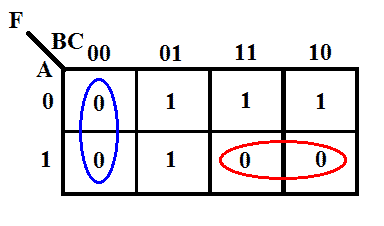
Espressione minima usando K-map

F = (B+C) (A̅+B̅)

L’espressione ottenuta è il prodotto minimo della forma somma. È ancora l’espressione Prodotto di somma, ma ha bisogno solo di 2 ingressi, due porte OR e una singola porta AND a 2 ingressi. Tuttavia, la forma canonica ha bisogno di 4 porte OR di 3 ingressi e 1 porta AND di 4 ingressi.

• Si può anche leggere: Feedback negativo e sistemi di amplificatori a feedback negativo

Progettazione schematica del prodotto di somma (POS)

Il prodotto di somma ha una specifica progettazione schematica di OR-AND. In OR-AND gli ingressi passano attraverso un array di porte OR che è il primo livello di porte, l’uscita del primo livello di porte OR passa attraverso il secondo livello della porta, che è una porta AND.

Il numero di ingressi e il numero di porte usate in questo disegno dipende dall’espressione che deve essere implementata.

La forma canonica consiste nel massimo numero di ingressi e porte possibili, tuttavia, la forma minima consiste nel minor numero possibile di ingressi e porte. Il disegno schematico della forma POS canonica e minima è dato di seguito.

Conversione da POS minimo a POS in forma canonica

Come sappiamo la forma canonica di POS ha termini massimi e i termini massimi contengono ogni ingresso sia complementato che non complementato. Quindi aggiungeremo ogni termine di somma con il prodotto degli input mancanti completati e non completati. Esempio della sua conversione è dato qui sotto.

Forma POS minima

F = (A̅+B̅) (B+C)

(A̅+B̅) termine manca l’ingresso C quindi aggiungeremo (CC̅) con esso. Il termine (B+C) manca dell’ingresso A quindi aggiungeremo (AA̅) con esso.

F = (A̅+B̅+CC̅) (B+C+AA̅)

F = (A̅+B̅+C)(A̅+B̅+C̅)(A+B+C)(A̅+B+C)

Questa espressione è ora in forma canonica: Contatore e tipi di contatori elettronici

Conversione da POS canonico a SOP

Il prodotto dell’espressione Somma può essere convertito nella forma Somma del prodotto solo se l’espressione è in forma canonica. POS canonico e SOP canonico sono interconvertibili, cioè possono essere convertiti l’uno nell’altro. Un esempio di conversione da POS a SOP è dato qui sotto.

F forma canonica POS

F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

Nella forma canonica ogni termine di somma è un termine massimo quindi può anche essere scritto come:

F = ∏(M0,M4,M6,M7)

Le rimanenti combinazioni di ingressi sono mintermini della funzione per cui il suo output è vero. Per convertirla in un’espressione SOP, per prima cosa cambieremo il simbolo in sommatoria (∑) e useremo i mintermini rimanenti.

F = ∑ (m1,m2,m3,m5)

Ora espanderemo il segno di sommatoria per formare l’espressione SOP canonica.

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

I termini Min sono il complemento dei termini Max per la stessa combinazione di ingressi.

Da canonico a minimo POS

Un prodotto canonico di espressione di somma può essere convertito in prodotto minimo di forma somma usando la mappa di Karnaugh (K-map). Un altro metodo per convertire il canonico in minimo è usando i teoremi dell’algebra booleana.

L’uso della K-map è molto facile ed è per questo che la K-map è preferita. Per l’espressione POS minima, gli 0 in K-map sono combinati in gruppi e l’espressione che otteniamo è completata poiché i gruppi sono fatti di ‘0’. Il suo esempio è stato fatto sopra.

Potresti anche leggere:

• Gate di logica digitale NOT Gate – Digital Inverter Logic Gate
• Exclusive-NOR (XNOR) Digital Logic Gate
• Digital Logic NOR Gate
• Digital Logic NAND Gate