” Quanto è grande una cellula di E. coli e qual è la sua massa?

Quanto è grande una cellula di E. coli e qual è la sua massa?

Modalità lettore

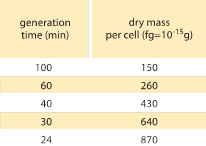
Tabella 1: Relazione tra massa batterica e tempo di divisione. La massa secca per cellula è data in funzione del tempo di generazione (raddoppio). Si suggerisce che la massa aumenti in modo approssimativamente esponenziale con il tasso di crescita, come originariamente osservato da M. Schaechter et al J. Gen. Microbiol., 19:592, 1958. Il peso secco delle cellule è stato calcolato utilizzando un valore di 173 µg per unità OD460 di un mL (BNID 106437). Il ceppo usato è B/r, un ceppo comunemente usato nei primi studi di fisiologia batterica. Valori presi da F. C. Neidhardt, “Escherichia coli and Salmonella: Cellular and Molecular Biology”, Vol. 1., Chapter 3, ASM Press, 1996.

La dimensione di un tipico batterio come l’E. coli serve come un comodo righello standard per caratterizzare le scale di lunghezza nella biologia molecolare e cellulare. Una “regola empirica” basata su generazioni di misurazioni al microscopio ottico ed elettronico per le dimensioni di una cellula di E. coli è di assegnarle un diametro di circa ≈1µm, una lunghezza di ≈2µm, e un volume di ≈1µm3 (1 fL) (BNID 101788). La forma può essere approssimata come uno sferocilindro, cioè un cilindro con calotte emisferiche. Dati il diametro e la lunghezza citati possiamo calcolare una stima più raffinata per il volume di ≈1,3 µm3 (5π/12 per essere precisi). La differenza tra questo valore e il valore della regola empirica citata sopra mostra il livello di incoerenza con cui viviamo comodamente quando usiamo le regole empiriche. Una delle vie più semplici per una stima della massa di un batterio è sfruttare il volume di ≈1 µm3 di una cellula di E. coli e assumere che abbia la stessa densità dell’acqua. Questa stima ingenua si traduce in un altro valore standard, cioè che un batterio come l’E. coli ha una massa di ≈1 pg (pico=10-12). Poiché la maggior parte delle cellule sono per circa 2/3 acqua (BNID 100044, 105482) e gli altri componenti, come le proteine, hanno una densità caratteristica di circa 1,3 volte la densità dell’acqua (BNID 101502, 104272) la conversione dal volume cellulare alla massa è accurata al 10% circa.

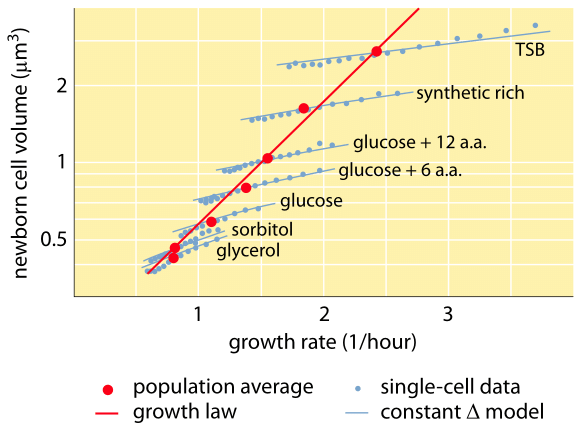
Fig. 1: Relazione tra volume cellulare e tasso di crescita. Usando la microscopia e i dispositivi microfluidici il volume cellulare può essere misurato a livello di singola cellula in varie condizioni, confermando che il volume cellulare medio cresce esponenzialmente con il tasso di crescita. Al contrario, la variazione tra le cellule per una data condizione scala in modo diverso. La variazione nel comportamento della singola cellula è usata per testare modelli di regolazione delle dimensioni delle cellule. (Adattato da S. Taheri-Araghi et al., Curr. Biol. 25:385, 2015.)

Uno dei risultati classici della fisiologia batterica sottolinea che la plasticità delle proprietà delle cellule deriva dalla dipendenza della massa cellulare dal tasso di crescita. Detto semplicemente, tassi di crescita più veloci sono associati a cellule più grandi. Questa osservazione si riferisce ai cambiamenti fisiologici in cui i media che aumentano il tasso di crescita producono anche cellule più grandi, come mostrato nella Figura 1. Questo è stato trovato vero anche geneticamente, dove studi di evoluzione sperimentale a lungo termine che hanno portato a tassi di crescita più veloci hanno mostrato volumi cellulari più grandi (BNID 110462). Queste osservazioni ci aiutano a sfatare il mito della “cellula” – dove le persone, spesso incautamente, usano misure su una cellula per fare inferenze su altri tipi di cellule o sullo stesso tipo di cellule in condizioni diverse. Gli studi classici di Dennis e Bremer hanno sistematizzato queste misurazioni e hanno trovato che la massa secca varia come mostrato nella tabella 1 da un valore medio di 148 fg per le cellule che si dividono ogni 100 minuti a 865 fg per quelle con un tempo di divisione di 24 minuti, indicando una differenza di oltre 5 volte a seconda del tasso di crescita. Una tendenza simile è stata vista in altri organismi (ad esempio per il lievito in erba, BNID 105103). A circa il 70% di acqua questi valori corrispondono a una gamma tra circa 0,4 e 2,5 µm3 in termini di volume. Come possiamo razionalizzare le dimensioni più grandi per le cellule che crescono a velocità più elevate? Questa domanda è tuttora oggetto di dibattito (Molenaar D. et al. MSB 5:323, 2009; Amir, A., Phys. Rev, Let., 112:208102, 2014). Le spiegazioni variano dal suggerire che ha un vantaggio nel modo in cui viene fatta l’allocazione delle risorse a sostenere che è in realtà solo un effetto collaterale di avere un periodo costruito di circa 60 minuti dal momento in cui una cellula decide che ha accumulato abbastanza massa per iniziare i preparativi per la divisione e fino a quando non finisce la replicazione del DNA e l’atto di divisione. Questo periodo di “ritardo” approssimativamente costante porta ad una dipendenza esponenziale della massa cellulare media dal tasso di crescita in questa linea di ragionamento (Amir, A., Phys. Rev, Let, 112:208102, 2014).

I metodi per misurare il volume delle cellule vanno dall’uso di un contatore Coulter ((BNID 100004), che infonde il volume in base alle variazioni di resistenza di un piccolo orifizio al passaggio di una cellula in esso, a misure più dirette utilizzando la microscopia a fluorescenza che misura la lunghezza e il diametro delle cellule in diverse condizioni (Figura 1 e BNID 106577, 111480). Sorprendentemente, il fatto che diversi laboratori non sempre convergono sugli stessi valori può essere dovuto a differenze nei metodi di calibrazione o a ceppi e condizioni di crescita esatte. Una capacità senza precedenti di misurare la massa delle cellule si ottiene pesando efficacemente le cellule su un cantilever microscopico. Come illustrato nella Figura 2A, il flusso del fluido viene utilizzato per forzare una cella avanti e indietro nel cantilever scavato. La misurazione sfrutta il fatto che la massa della cellula influenza la frequenza di oscillazione del cantilever. Questa frequenza può essere misurata con un’accuratezza fenomenale e utilizzata per dedurre le masse con una precisione di un femtogrammo. Cambiando la direzione del flusso del liquido, la cellula viene intrappolata per minuti o più e il suo tasso di accumulo di massa viene misurato continuamente a livello di singola cellula. Nell’applicazione iniziale di questa tecnica è stato dimostrato che le cellule singole che sono più grandi accumulano anche la massa più velocemente, facendo luce su una questione di lunga data: la crescita cellulare è lineare con il tempo o più appropriatamente descritta da un andamento approssimativamente esponenziale? Le differenze possono essere minime, ma con queste capacità rivoluzionarie si è visto chiaramente che quest’ultimo scenario rappresenta meglio la situazione in diversi tipi di cellule testate, come mostrato nella Figura 2B.

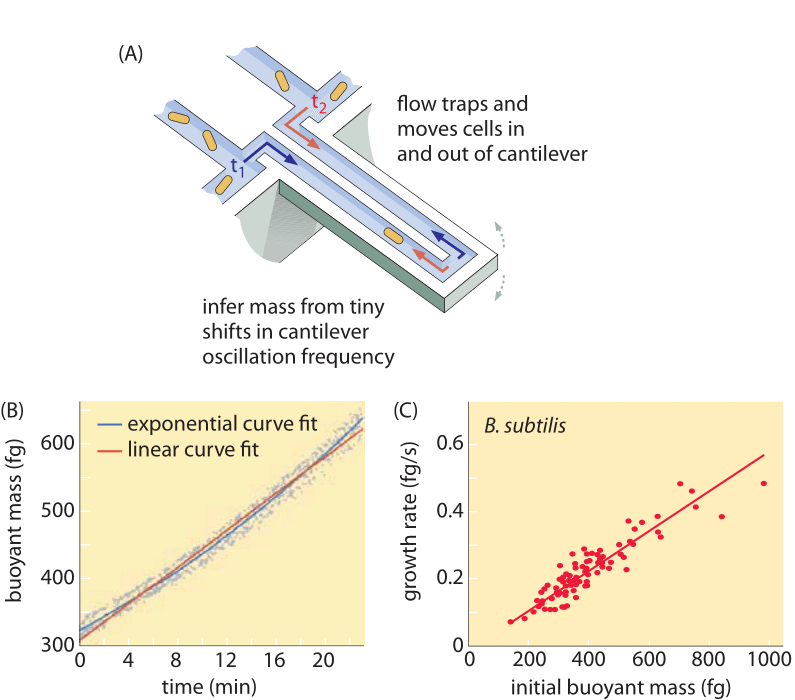
Fig. 2: Utilizzo della massa galleggiante per misurare la crescita di singole cellule. (A) Un cantilever su scala micrometrica oscilla ad alta frequenza e la massa delle cellule può essere determinata dai cambiamenti nella frequenza di oscillazione. (B) Misurato nel tempo, questo si traduce in una curva di accumulo della massa delle singole cellule come mostrato. (C) Qui sono mostrate cellule di B. subtilis. Un confronto tra le previsioni dei modelli di crescita lineare ed esponenziale sono mostrati come best fit. La somiglianza dimostra quanto siano vicini i due modelli su un intervallo di solo due volte l’aumento nel corso del ciclo cellulare. Il peso secco delle cellule è circa 4 volte la massa galleggiante. (Adattato da M. Godin et al., Nature Meth. 7:387, 2010.)