Perché 0,999… è uguale a 1?!

Un altro modo di pensare ai termini della nostra sommatoria è che ogni termine successivo è ottenuto moltiplicando il termine precedente per un rapporto comune.

Questo significa che abbiamo una serie geometrica che converge ad a/(1 – r) dove a è il primo valore della serie e r è il rapporto per cui moltiplichiamo per ottenere il termine successivo.

La convergenza in una serie significa semplicemente che la serie continuerà ad avvicinarsi sempre più ad un valore specifico man mano che si aggiungono sempre più termini alla serie. La serie si avvicina infinitesimamente al valore di convergenza. Su una scala infinita, la convergenza diventa uguaglianza.

Nel nostro caso, iniziamo con 1/10 e moltiplichiamo per 1/10 ogni volta, quindi sia a che r = 1/10.

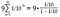
Completa l’aritmetica sul lato destro.

Ora abbiamo dimostrato formalmente che 0.999… converge a o è uguale a 1.

Pensieri finali & Ispirazione

Se questo ti sembra strano, va bene! Sapete che due numeri diversi, dovrebbero in effetti essere numeri diversi. La natura controintuitiva di questo problema è inerente alla stranezza che accompagna il lavoro con l’infinito.

Anche in un problema semplice come questo, ti stai muovendo dai confini di ciò che è tangibile per il cervello umano su una scala che è in un certo senso oltre la nostra comprensione. Come esseri finiti, possiamo afferrare il concetto di infinito o di eternità, ma non possiamo mai sperimentarlo veramente. Il che significa che spesso ciò che sappiamo essere vero nel nostro mondo finito, si comporta diversamente a livello infinito.

Accettare la transizione da una matematica facilmente scopribile e riproducibile a ciò che può essere solo testato e immaginato nella nostra mente fa parte della bellezza e della meraviglia della matematica.

Quindi non prendete la lezione di oggi al valore nominale e scrollate le spalle.

Lasciate che ci sia uno strato di nebbia tra voi e la perfetta comprensione. Lasciate che la vostra mente sia sconvolta dal fatto che l’infinito si comporta in modo strano. E lasciate che vi faccia desiderare più comprensione e soprattutto più matematica.

Grazie per aver letto e riflettuto sull’infinito con me oggi!