Funzioni o Mappatura

Ora, in funzioni o mappatura studieremo un tipo speciale di relazioni chiamate funzioni o mappatura. Per capirle, prendiamo alcuni esempi di vita reale.

Tutte queste domande hanno
uniche risposte. Vediamo come possiamo mettere in relazione
questo nella mappatura dell’apprendimento.

● Da dove sorge il sole?

Est

● Qual è la capitale dell’India?

Delhi

● Qual è il successore di 4?

5

● Qual è la somma di 5 e 3?

8

Mapping o funzioni:

Se A e B sono due insiemi non vuoti, allora una relazione ‘f’ dall’insieme A all’insieme B è detta funzione o mapping,
● se ogni elemento dell’insieme A è associato a un unico elemento dell’insieme B.

● La funzione ‘f’ da A a B è indicata con f : A → B.

● Se f è una funzione da A a B e x ∈ A, allora f(x) ∈ B dove f(x) è detta immagine di x sotto f e x è detta pre immagine di f(x) sotto ‘f’.

Nota:

Perché f sia una mappatura da A a B:

● Ogni elemento di A deve avere immagine in B. La figura adiacente non rappresenta una mappatura poiché l’elemento d nell’insieme A non è associato a nessun elemento dell’insieme B.

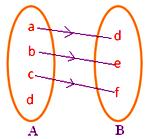
● Nessun elemento di A deve avere più di una immagine. La figura accanto non rappresenta una mappatura poiché l’elemento b dell’insieme A è associato a due elementi d, f dell’insieme B.

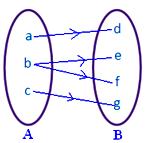
● Elementi diversi di A possono avere la stessa immagine in B. La figura adiacente rappresenta una mappatura.

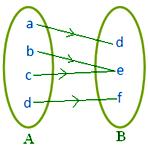
Nota:

Ogni mappatura è una relazione ma ogni relazione può non essere una mappatura.

Funzione come tipo speciale di relazione:

Ricordiamo e rivediamo la funzione come tipo speciale di relazione supponiamo che A e B siano due insiemi non vuoti, allora una regola ‘f’ che associa ogni elemento di A con un unico elemento di B è chiamata funzione o mappatura da A a B.
Se ‘f’ è una mappatura da A a B,

la esprimiamo come f: A → B

la leggiamo come ‘f’ è una funzione da A a B.
Se ‘f ‘ è una funzione da A a B e x∈A e y∈B, allora diciamo che y è l’immagine dell’elemento x sotto la funzione ‘f ‘ e la denotiamo con f(x).
Perciò, lo scriviamo come y = f(x)

Qui, l’elemento x è chiamato la pre-immagine di y.

Quindi, per una funzione da A a B.
● A e B devono essere non vuoti.

● Ogni elemento di A dovrebbe avere immagine in B.

● Nessun elemento di ‘A’ dovrebbe avere più di una immagine in ‘B’.
Nota:

● Due o più elementi di A possono avere la stessa immagine in B.

● f : x → y significa che sotto la funzione di ‘f’ da A a B, un elemento x di A ha immagine y in B.

● È necessario che ogni immagine f sia in B ma ci possono essere alcuni elementi in B che non sono immagini f di nessun elemento di A.

● Relazioni e Mappature

Pacco ordinato

Prodotto cartesiano di due insiemi

Relazione

Dominio e intervallo di una relazione

Funzioni o Mappature

Dominio Co-dominio e intervallo di una funzione

● Relazioni e mappatura – Fogli di lavoro

Foglio di lavoro sulla relazione matematica

Foglio di lavoro sulle funzioni o sulla mappatura

Problemi di matematica di 7° grado

Pratica di matematica di 8° grado
Da Funzioni o Mappatura a HOME PAGE