E se i tuoi dati NON sono normali?

Introduzione

È la settimana di Halloween, e tra dolcetti e scherzetti, noi geek dei dati stiamo ridacchiando di questo simpatico meme sui social media.

Pensi che sia uno scherzo? Lasciate che vi dica che non c’è niente da ridere. Fa paura, nello spirito di Halloween!

Se non possiamo assumere che la maggior parte dei nostri dati (di origine commerciale, sociale, economica o scientifica) siano almeno approssimativamente “normali” (cioè generati da un processo gaussiano o da una somma di più processi di questo tipo), allora siamo condannati!

Ecco una brevissima lista di cose che non saranno valide,

• Tutto il concetto di sei-sigma
• La famosa regola 68-95-99.7
• Il ‘sacro’ concetto di p=0.05 (deriva dall’intervallo 2 sigma) nell’analisi statistica

Basta spaventarsi? Parliamone ancora…

L’onnipotente e onnipresente distribuzione normale

Teniamo questa sezione breve e dolce.

La distribuzione normale (gaussiana) è la distribuzione di probabilità più conosciuta. Ecco alcuni link agli articoli che descrivono la sua potenza e la sua ampia applicabilità,

• Perché gli scienziati di dati amano la gaussiana

• Come dominare la parte di statistica del tuo colloquio di Data Science
• Cosa c’è di così importante nella distribuzione normale?

A causa della sua comparsa in vari domini e del Teorema del Limite Centrale (CLT), questa distribuzione occupa un posto centrale nella scienza dei dati e nell’analitica.

Quindi, qual è il problema?

Questo è tutto perfetto, qual è il problema?

Il problema è che spesso puoi trovare una distribuzione per il tuo specifico set di dati, che può non soddisfare la normalità, cioè le proprietà di una distribuzione normale. Ma a causa dell’eccessiva dipendenza dal presupposto della normalità, la maggior parte dei framework di business analytics sono fatti su misura per lavorare con insiemi di dati distribuiti in modo normale.

È quasi radicato nella nostra mente subconscia.

Diciamo che vi viene chiesto di rilevare il controllo se un nuovo lotto di dati da qualche processo (ingegneria o business) ha senso. Per ‘senso’, si intende se i nuovi dati appartengono, cioè se sono all’interno del ‘range atteso’.

Qual è questa ‘aspettativa’? Come quantificare l’intervallo?

Automaticamente, come se fossimo guidati da un impulso subconscio, misuriamo la media e la deviazione standard del campione di dati e procediamo a controllare se il nuovo dato rientra in un certo intervallo di deviazioni standard.

Se dobbiamo lavorare con un limite di confidenza del 95%, allora siamo felici di vedere i dati che rientrano in 2 deviazioni standard. Se abbiamo bisogno di un limite più severo, controlliamo 3 o 4 deviazioni standard. Calcoliamo Cpk, o seguiamo le linee guida six-sigma per il livello di qualità ppm (parti per milione).

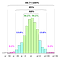
Tutti questi calcoli sono basati sull’assunzione implicita che i dati della popolazione (NON il campione) seguano la distribuzione gaussiana cioè il processo fondamentale, da cui deriva la distribuzione Gaussiana.cioè il processo fondamentale, da cui tutti i dati sono stati generati (nel passato e nel presente), è governato dal modello sul lato sinistro.

Ma cosa succede se i dati seguono il modello sul lato destro?

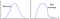
Ovvero, questo e… quello?

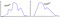
C’è un limite più universale quando i dati NON sono normali?

Alla fine della giornata, avremo ancora bisogno di una tecnica matematicamente valida per quantificare il nostro limite di fiducia, anche se i dati non sono normali. Ciò significa che il nostro calcolo potrebbe cambiare un po’, ma dovremmo comunque essere in grado di dire qualcosa del genere-

“La probabilità di osservare un nuovo punto di dati a una certa distanza dalla media è tale e quale…”

Ovviamente, dobbiamo cercare un limite più universale dei cari limiti gaussiani di 68-95-99.7 (corrispondenti a 1/2/3 deviazioni standard di distanza dalla media).

Fortunatamente, c’è un tale limite chiamato “Chebyshev Bound”.

Che cos’è il Chebyshev Bound e come è utile?

La disuguaglianza di Chebyshev (chiamata anche disuguaglianza di Bienaymé-Chebyshev) garantisce che, per un’ampia classe di distribuzioni di probabilità, non più di una certa frazione di valori può essere più di una certa distanza dalla media.

Specificamente, non più di 1/k² dei valori della distribuzione può essere più di k deviazioni standard lontano dalla media (o equivalentemente, almeno 1-1/k² dei valori della distribuzione sono entro k deviazioni standard dalla media).

Si applica a tipi virtualmente illimitati di distribuzioni di probabilità e funziona su un presupposto molto più rilassato della Normalità.

Come funziona?

Anche se non sai nulla del processo segreto dietro i tuoi dati, c’è una buona probabilità che tu possa dire quanto segue,

“Sono sicuro che il 75% di tutti i dati dovrebbe cadere entro 2 deviazioni standard dalla media”,

Oppure,

Sono sicuro che l’89% di tutti i dati dovrebbe cadere entro 3 deviazioni standard dalla media”.

Ecco come appare per una distribuzione dall’aspetto arbitrario,

Come applicarlo?

Come puoi intuire ora, la meccanica di base della tua analisi dei dati non ha bisogno di cambiare un po’. Raccoglierete ancora un campione di dati (più grande è meglio è), calcolerete le stesse due quantità che siete abituati a calcolare – media e deviazione standard, e poi applicherete i nuovi limiti invece della regola 68-95-99.7.

La tabella appare come segue (qui k denota tante deviazioni standard dalla media),

Un video dimostrativo della sua applicazione è qui,

Qual è la fregatura? Perché la gente non usa questo limite “più universale”?

È ovvio quale sia la fregatura guardando la tabella o la definizione matematica. La regola di Chebyshev è molto più debole della regola gaussiana per quanto riguarda la messa in gioco dei dati.

Segue un modello 1/k² rispetto ad un modello esponenzialmente decrescente per la distribuzione normale.

Per esempio, per mettere in gioco qualcosa con il 95% di confidenza, è necessario includere dati fino a 4,5 deviazioni standard contro Solo 2 deviazioni standard (per la normale).

Ma può ancora salvare la giornata quando i dati non assomigliano affatto a una distribuzione normale.

C’è qualcosa di meglio?

C’è un altro limite chiamato “Chernoff Bound”/disuguaglianza di Hoeffding che dà una distribuzione di coda esponenzialmente netta (rispetto al 1/k²) per somme di variabili casuali indipendenti.

Questa può anche essere usata al posto della distribuzione gaussiana quando i dati non sembrano normali, ma solo quando abbiamo un alto grado di fiducia che il processo sottostante sia composto da sottoprocessi che sono completamente indipendenti l’uno dall’altro.

Purtroppo, in molti casi sociali e aziendali, i dati finali sono il risultato di un’interazione estremamente complicata di molti sottoprocessi che possono avere una forte interdipendenza.

Sommario

In questo articolo, abbiamo imparato a conoscere un particolare tipo di vincolo statistico che può essere applicato alla più ampia distribuzione possibile di dati indipendentemente dal presupposto della normalità. Questo è utile quando sappiamo molto poco sulla vera origine dei dati e non possiamo assumere che segua una distribuzione gaussiana. Il limite segue una legge di potenza invece di una natura esponenziale (come la gaussiana) e quindi è più debole. Ma è uno strumento importante da avere nel proprio repertorio per analizzare qualsiasi tipo arbitrario di distribuzione dei dati.