2.12: Equazione di Van der Waals

Un’equazione dovuta a van der Waals estende l’equazione dei gas ideali in modo semplice. L’equazione di Van der Waals è

Adatta i dati di pressione-volume-temperatura per un gas reale meglio di quanto faccia l’equazione del gas ideale. L’adattamento migliorato è ottenuto introducendo due parametri (designati “\(a\)” e “\(b\)”) che devono essere determinati sperimentalmente per ogni gas. L’equazione di Van der Waals è particolarmente utile nel nostro sforzo di comprendere il comportamento dei gas reali, perché incarna un semplice quadro fisico per la differenza tra un gas reale e un gas ideale.

Nella derivazione della legge di Boyle dalle leggi di Newton, si assume che le molecole del gas non interagiscano tra loro. Semplici argomenti dimostrano che questo può essere vero solo approssimativamente. Le molecole di gas reali devono interagire l’una con l’altra. A brevi distanze si respingono a vicenda. A distanze un po’ più lunghe, si attraggono a vicenda. L’equazione del gas ideale può anche essere derivata dalle assunzioni di base che abbiamo fatto nel § 10 mediante un’applicazione della teoria della termodinamica statistica. Facendo diverse ipotesi sulle proprietà molecolari, possiamo applicare la termodinamica statistica per derivare l’equazione di van der Waals. Le ipotesi richieste sono che le molecole occupino un volume finito e che si attraggano a vicenda con una forza che varia come l’inverso di una potenza della distanza tra loro. (La forza attrattiva è di solito assunta come proporzionale a \(r^{-6}\).)

Per riconoscere che le molecole di gas reali si attraggono e si respingono a vicenda, dobbiamo solo ricordare che qualsiasi gas può essere liquefatto riducendo la sua temperatura e aumentando la pressione applicata ad esso. Se raffreddiamo ulteriormente il liquido, questo si congela e diventa un solido. Ora, due caratteristiche distintive di un solido sono che conserva la sua forma e che è quasi incomprimibile. Attribuiamo l’incomprimibilità di un solido alle forze repulsive tra le molecole che lo compongono; esse sono così vicine tra loro che le forze repulsive tra loro sono diventate importanti. Per comprimere il solido, le molecole devono essere spinte ancora più vicine, il che richiede una forza smodata. D’altra parte, se lanciamo un cubetto di ghiaccio dall’altra parte della stanza, tutte le molecole d’acqua che lo compongono volano insieme attraverso la stanza. Evidentemente, le molecole d’acqua nel solido sono attratte l’una dall’altra, altrimenti andrebbero tutte per la loro strada – lanciare il cubetto di ghiaccio sarebbe come lanciare una manciata di sabbia secca. Ma le molecole d’acqua sono le stesse molecole qualunque sia la temperatura o la pressione, quindi se ci sono forze di attrazione e repulsione tra loro nel solido, queste forze devono essere presenti anche nelle fasi liquida e gassosa.

Nella fase gassosa, le molecole sono distanti tra loro; nella fase liquida o solida, sono impacchettate insieme. Al punto di ebollizione, il volume di un liquido è molto inferiore al volume del gas da cui è condensato. Al punto di congelamento, il volume di un solido è solo leggermente diverso dal volume del liquido da cui è congelato, ed è certamente maggiore di zero. Queste osservazioni banali si spiegano facilmente supponendo che ogni molecola abbia un volume caratteristico. Possiamo capire che questo, a sua volta, è una conseguenza della natura delle forze intermolecolari; evidentemente, queste forze diventano più forti al diminuire della distanza tra una coppia di molecole. Poiché un liquido o un solido occupa un volume definito, la forza repulsiva deve aumentare più rapidamente della forza attrattiva quando la distanza intermolecolare è piccola. Spesso è utile parlare del volume molare di una fase condensata. Per volume molare, si intende il volume di una mole di una sostanza pura. Il volume molare di una fase condensata è determinato dalla distanza intermolecolare alla quale c’è un equilibrio tra le forze intermolecolari di attrazione e repulsione.

Evidentemente le molecole sono molto vicine tra loro nelle fasi condensate. Se supponiamo che gli spazi vuoti tra le molecole siano trascurabili, il volume di una fase condensata è circa uguale al numero di molecole nel campione moltiplicato per il volume di una singola molecola. Allora il volume molare è il numero di Avogadro per il volume occupato da una molecola. Se conosciamo la densità, D, e la massa molare, \(\overline{M}), possiamo trovare il volume molare, \(\overline{V}), come

Il volume occupato da una molecola, V\({}_{molecola}\, diventa

\

La pressione e il volume che appaiono nell’equazione di van der Waals sono la pressione e il volume del gas reale. Possiamo mettere in relazione i termini dell’equazione di van der Waals con l’equazione del gas ideale: È utile pensare ai termini \(\sinistra(P+{{an}^2}/{V^2}\destra)\) e \(\sinistra(V-nb\destra)\ come la pressione e il volume di un ipotetico gas ideale. Cioè

&=nRT \end{align*}]

Allora abbiamo

Deriviamo l’equazione del gas ideale da un modello in cui le molecole sono masse puntuali non interagenti. Quindi il volume di un gas ideale è il volume occupato da un gas le cui singole molecole hanno volume zero. Se le singole molecole di un gas reale occupano effettivamente un volume \(b}/{\overline{N}}}, allora \(n\) moli di esse occupano effettivamente un volume

L’equazione di Van der Waals dice che il volume di un gas reale è il volume che sarebbe occupato da masse puntiformi non interagenti, \(V_ gas ideale), più il volume effettivo delle molecole del gas stesso. (Quando i dati per le molecole di gas reali sono adattati all’equazione di van der Waals, il valore di \(b\) è di solito un po’ più grande del volume stimato dalla densità del liquido e dal peso molecolare. Vedi problema 24.)

Similmente, abbiamo

Possiamo capire questo come una conseguenza logica delle interazioni attrattive tra le molecole del gas reale. Con \(a>0\), si dice che la pressione del gas reale è inferiore alla pressione del gas ideale ipotetico, di una quantità che è proporzionale a \({sinistra({n}/{V}destra)}^2\). La costante di proporzionalità è \(a\). Poiché \({n}/{V}}) è la densità molare (moli per unità di volume) delle molecole di gas, è una misura della concentrazione. Il numero di collisioni tra molecole dello stesso tipo è proporzionale al quadrato della loro concentrazione. (Consideriamo questo punto in modo più dettagliato nei capitoli 4 e 5.) Quindi \(\sinistra({n}/{V}destra)}^2\) è una misura della frequenza con cui le molecole di gas reali entrano in stretto contatto tra loro. Se si attraggono l’un l’altra quando si avvicinano, l’effetto di questa attrazione dovrebbe essere proporzionale a \({\left({n}/{V}right)}^2\). Quindi l’equazione di van der Waals è coerente con l’idea che la pressione di un gas reale è diversa dalla pressione del gas ideale ipotetico di una quantità che è proporzionale alla frequenza e alla forza delle interazioni attrattive.

Ma perché le interazioni attrattive dovrebbero avere questo effetto; perché la pressione del gas reale dovrebbe essere inferiore a quella del gas ideale ipotetico? Forse il modo migliore per sviluppare un quadro qualitativo è riconoscere che le forze intermolecolari attrattive tendono a far raggruppare le molecole di gas. Dopo tutto, sono queste forze attrattive che causano l’aggregazione delle molecole in un liquido a basse temperature. Al di sopra del punto di ebollizione, la capacità delle molecole di gas di andare per la loro strada limita gli effetti di questa tendenza; tuttavia, anche nel gas, le forze attrattive devono agire in un modo che tende a ridurre il volume occupato dalle molecole. Poiché il volume occupato dal gas è dettato dalle dimensioni del contenitore, e non dalle proprietà del gas stesso, questa tendenza a raggrupparsi si esprime con una diminuzione della pressione.

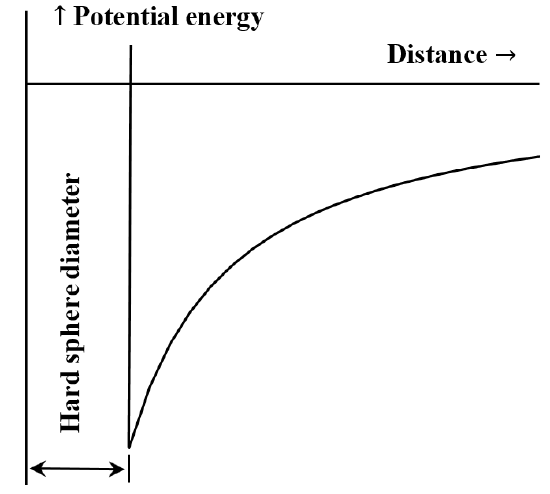
È spesso utile descrivere l’interazione tra particelle o società chimiche in termini di un diagramma di energia potenziale in funzione della distanza. L’equazione di van der Waals corrisponde al caso in cui l’interazione repulsiva tra le molecole è inesistente finché le molecole non vengono a contatto. Una volta che entrano in contatto, l’energia richiesta per avvicinarle ancora di più diventa arbitrariamente grande. Spesso questo viene descritto dicendo che si comportano come “sfere dure”. La forza attrattiva tra due molecole diminuisce all’aumentare della distanza tra loro. Quando sono molto distanti l’interazione attrattiva è molto piccola. Diciamo che l’energia di interazione è zero quando le molecole sono infinitamente lontane. Se inizialmente abbiamo due molecole molto separate, stazionarie, che si attraggono reciprocamente, esse si muoveranno spontaneamente l’una verso l’altra, guadagnando energia cinetica mentre vanno. La loro energia potenziale diminuisce man mano che si avvicinano l’una all’altra, raggiungendo il suo valore minimo quando le molecole entrano in contatto. Così, l’equazione di van der Waals implica il diagramma dell’energia potenziale in funzione della distanza abbozzato nella figura 5.

.