Sum Of Product (SOP) & Product Of Sum (POS)
On november 10, 2021 by adminProduct Of Sum (POS) & Sum Of Product (SOP)
Tartalomjegyzék
Sum Of Product (SOP)
A Sum Of Product az SOP rövidített formája. A Sum of product forma egy olyan kifejezésforma a Boole-algebrában, amelyben a bemenetek különböző terméktételei összegződnek. Ez a termék nem aritmetikai szorzás, hanem Boole logikai ÉS, az összeg pedig Boole logikai VAGY.
Az SOP jobb megértéséhez ismernünk kell a min termet.
Min term
Minterm azt a termet jelenti, amely a bemenetek minimális számú kombinációjára igaz. Ez csak egy bemeneti kombinációra igaz.
Mivel az AND kapu is csak akkor ad igazat, ha minden bemenete igaz, így mondhatjuk, hogy a min termek a bemeneti kombinációk ÉS-je, mint az alábbi táblázatban.
3 bemenetnek 8 különböző kombinációja van. Minden kombinációnak van egy min terminusa, amelyet kis m-gyel jelölünk, és a kombináció tizedes kombinációs száma van írva az index alatt. Mindegyik minterm csak az adott bemeneti kombinációra lesz igaz.
- Azt is elolvashatja:
A termékösszeg (SOP) formáinak típusai
A termékösszegnek néhány különböző formája van.
- Kanonikus SOP forma
- Nem kanonikus SOP forma
- Minimális SOP forma
Kanonikus SOP forma
Ez a szorzatösszeg standard formája. Úgy képezzük, hogy O Ring azon függvény mintermeit képezi, amelyre a kimenet igaz. Ezt a formát a Min-terminusok összegének vagy kanonikus diszjunktív normálformának (CDNF) is nevezik. Ez csak egy fantázianév. A “kanonikus” azt jelenti, hogy “szabványos”, a “diszjunktív” pedig azt jelenti, hogy “logikai VAGY egyesítés”.
A kanonikus SOP-kifejezést a ∑ összegző jel és a szögletes zárójelben lévő mintermák képviselik, amelyekre a kimenet igaz.
Egy függvény igazságtáblája például az alábbiakban látható.

Ezért a függvényért a kanonikus SOP kifejezés
F = ∑( m1, m2, m3, m5 )
Ami azt jelenti, hogy a függvény igaz a {1, 2, 3, 5} mintermekre.
Az összegzés kibővítésével megkapjuk.
F = m1 + m2 + m3 + m5
Most a min tagokat a kifejezésbe helyezve
F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C
A kanonikus forma minden bemenetet tartalmaz akár kiegészítve, akár nem kiegészítve a terméktételeiben.
Az is olvasható: Alkalmazások
Nem kanonikus SOP forma
Amint a neve is mutatja, ez a forma a SOP-kifejezések nem szabványosított formája. A termékkifejezések nem a min kifejezések, hanem egyszerűsítettek. Vegyük példának a fenti függvényt kanonikus formában.
F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C
F = A̅B̅C + A̅B(C̅ + C) + AB̅C
F = A̅B̅C + A̅B(C̅ + C) + AB̅C
F = A̅B̅C + + A̅B̅C A̅B(1) + AB̅C
F = A̅B̅C + A̅B + AB̅C
Ez a kifejezés még mindig szorzatösszeg formában van, de már nemkanonikus vagy nem szabványosított formában.
Minimális SOP forma
Ez a forma a függvény legegyszerűbb SOP kifejezése. Ez is egy nem kanonikus forma. A minimális SOP-formát a Boole algebrai tételek segítségével lehet elkészíteni, de nagyon könnyen elkészíthető a Karnaugh-térkép (K-térkép) segítségével.
A minimális SOP-formát azért részesítik előnyben, mert a kapuk és bemeneti vonalak minimális számát használja. kereskedelmi szempontból előnyös a kompakt mérete, gyors sebessége és alacsony gyártási költsége miatt.
Vegyünk egy példát a fent megadott függvényre kanonikus formában.

A K-térképét az alábbiakban adjuk meg.
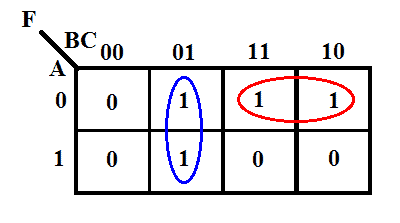
A K-térkép szerint a kimeneti kifejezés a következő lesz
F = B̅C + A̅B
Ez a legegyszerűbb & optimalizált kifejezés az említett függvényre. Ez a kifejezés csak két 2 bemenetű ÉS kaput & egy 2 bemenetű VAGY kaput igényel. A kanonikus formához azonban négy 3-bemenetű ÉS kapura & egy 4-bemenetű VAGY kapura van szükség, ami viszonylag költségesebb, mint a minimális forma megvalósítása.
- Azt is olvashatja: & Johnson számláló – felépítés & Működés
Sum Of Product (SOP)
SOP kifejezés 2 szintű AND-OR kialakítást valósít meg, amelyben az 1. szintű kapu AND kapu követi a 2. szintű kaput, amely OR kapu. A SOP-kifejezés sematikus tervezése AND-kapuk & egy OR-kaput igényel.
Minden SOP-kifejezés némileg azonos kialakítású, azaz minden bemenet AND-kapun megy keresztül, majd ezen AND-kapuk kimenete egy OR-kapun keresztül áramlik, amint az az alábbi ábrán látható.
A bemenetek száma és az AND-kapuk száma attól függ, hogy milyen kifejezést hajtunk végre.
Egy függvény kanonikus és minimális SOP kifejezésének tervezésére az alábbi példa látható.
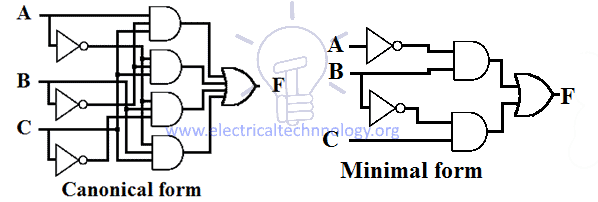
Minimal SOP formából kanonikus SOP formába való átalakítás
A minimális vagy bármilyen nem kanonikus formából kanonikus formába való átalakítás nagyon egyszerű.
Mint tudjuk, a kanonikus formának min terminusai vannak & A min terminus az összes bemenetből áll, akár kiegészítve, akár nem kiegészítve. Tehát a minimális SOP minden terminusát megszorozzuk a hiányzó bemenet kiegészített és nem kiegészített formájának összegével. A fenti függvény minimális SOP formában történő átalakítására az alábbi példa látható:
Minimális SOP forma
F = A̅B + B̅C
A̅B kifejezésből hiányzik a C bemenet. Tehát A̅B-t megszorozzuk (C+C̅), mert (C+C̅ = 1). A B̅C kifejezésből hiányzik az A bemenet. Így azt (A+A̅)
F = A̅B(C + C̅) + B̅C(A + A̅)
F = A̅BC + A̅BC̅ + AB̅C + A̅B̅C
Most ez a kifejezés kanonikus formában van.
Konvertálás kanonikus SOP-ból kanonikus POS-ba
A szabványos SOP kifejezés átalakítható szabványos POS (összeg szorzata) kifejezéssé. Például a fenti függvény kanonikus SOP formában
F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C
F = ∑ ( m1, m2, m3, m5 )
A függvény többi tagja olyan maxterm, amelynek kimenete hamis. Ezek a maxtermek az M0,M4,M6,M7. Ezeket a max kifejezéseket a POS kifejezésben e max kifejezések szorzataként fogjuk használni. A termék szimbóluma ∏.
F = ∏ ( M0, M4, M6, M7)
F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+B̅+C̅)
A Max kifejezések a mintermek komplementerei. Ezért M0=(A+B+C).
- Azt is elolvashatod:
Konvertálás a kanonikus SOP-ból a minimális SOP-ba
A kanonikus SOP átalakítható minimális SOP-ba. A Karnaugh-térkép vagy a Boole algebrai tételek segítségével alakítható át. A K-térképes módszer nagyon egyszerű, és a példáját a fentiekben a minimális SOP formában végeztük el.
Summa produktuma
A Summa produktuma rövidítve POS.
A Summa produktuma olyan forma, amelyben a bemenetek különböző összegtermeinek szorzatát vesszük. Ezek nem aritmetikai szorzat és összeg, hanem logikai Boolean AND és OR, illetve OR.
Az összegtermék jobb megértéséhez ismernünk kell a Max termet.
Max term
A Max term azt a termet vagy kifejezést jelenti, amely a bemenetek maximális számú kombinációjára igaz, vagy amely a bemenetek csak egy kombinációjára hamis.
Az OR kapu ugyanis szintén csak egy bemeneti kombinációra ad hamisat. Tehát a Maxterm vagy a komplementer vagy a nem komplementer bemenetek OR-ja.
Az alábbiakban 3 bemeneti változóra vonatkozó maximális kifejezések vannak megadva.
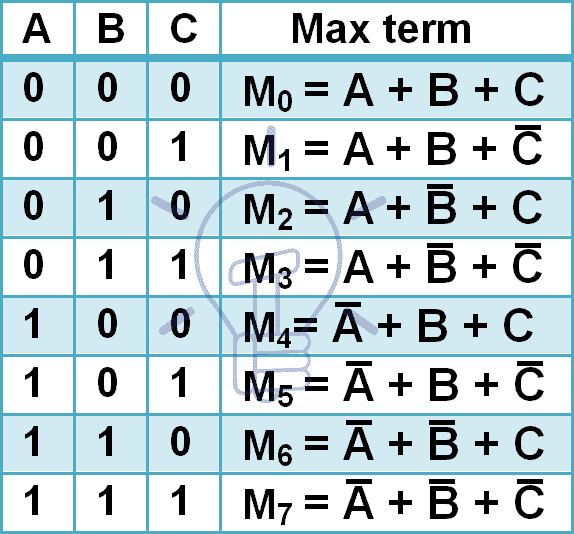
3 bemenetnek 8 különböző kombinációja van, tehát 8 maxterm lesz. A maxtermeket nagy M betűvel és tizedes kombinációs számmal jelöljük az indexben, ahogy a fenti táblázatban látható.
A maxtermekben minden bemenet komplementer, mert a maxterm csak akkor ad “0”-t, ha az említett kombinációt alkalmazzuk, és a maxterm a minterm komplementere.
M3 = m̅3
M3 = (A̅BC)’
M3 = A + B̅ +C̅ DE Morgan törvénye
Ezért A=0 esetén Maxterm A & A=1 esetén Maxterm A̅.
Azt is olvashatja: Flip-Flops – SR, D, JK és T Flip-Flops
A Product Of Sum formák típusai
A Product Of Sum formáknak különböző típusai vannak.
- Kanonikus POS forma
- Nem – kanonikus forma
- Minimális POS forma
Kanonikus POS forma
Ez a maximális terminus terméke vagy kanonikus konjunktív normál forma (CCNF) néven is ismert. A kanonikus azt jelenti, hogy normális, a konjunktív pedig azt, hogy metszet.
Ebben a formában a Maxtermák ÉS együtt vannak, amelyeknél a kimenet hamis.
A kanonikus POS-kifejezést ∏ és a Maxtermákat, amelyeknél a kimenet hamis, zárójelben ábrázoljuk, ahogy az alábbi példában látható.

F = ∏ (M0, M4, M6, M7)
A termék kiterjesztése
F = M0.M4.M6.M7
Max kifejezések beillesztése
F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅+C)
A kanonikus forma minden bemenetet vagy kiegészítve vagy nem kiegészítve tartalmaz minden egyes összegtételében.
- Az is olvasható:
Nem – kanonikus forma
A nem szabványos formában lévő összegkifejezés szorzatát nem kanonikus formának nevezzük.
Vegyük példának a fent megadott függvényt.
F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)
F = (B+C) (A̅+B̅+C)(A̅+B̅+C̅)
Az azonos, de megfordított kifejezések két Max kifejezésből eliminálódnak és egyetlen kifejezést alkotnak, hogy bizonyítsuk itt egy példa.
= (A+B+C) (A̅+B+C)
= AA̅+AB+AC+A̅B+BB+BC+A̅C+BC+CC
= 0+AB+AC+A̅B+A̅B+A̅C+B+BC+C
= A(B+C)+A̅(B+C)+B(1+C)+C
= (B+C)(A+A̅)+B(1)+C
= (B+C)(0)+B+C
= B+C
Az elért kifejezés még mindig az összegtermék formában van, de ez nemkanonikus forma.
Minimális POS forma
Ez a POS kifejezés legegyszerűsített és optimalizált formája, amely nem kanonikus. A Minimal Product of Sum forma a Boole algebrai tételek segítségével érhető el, mint a fenti nem kanonikus példában. A minimális POS-forma elérésének másik módszere a Karnaugh-térkép használata, amely viszonylag egyszerűbb, mint a Boole algebrai tételek használata.
A minimális POS-forma kevesebb bemenetet és logikai kaput használ a megvalósítás során, ezért előnyben részesítik a kanonikus formával szemben a kompakt, gyors és olcsó megvalósítás miatt.
Vegyük példának a fent megadott függvényt
A függvény K-térképe
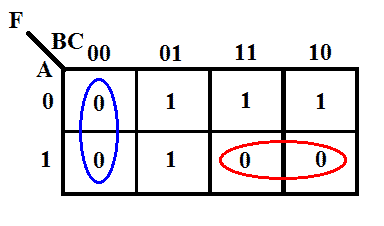
Minimális kifejezés K-térképpel
F = (B+C) (A̅+B̅)
Az elért kifejezés az összegforma minimális szorzata. Ez még mindig Product of Sum kifejezés De csak 2 bemenetű két OR kapura és egyetlen 2 bemenetű AND kapura van szüksége. A kanonikus formához azonban 4 db 3 bemenetű VAGY kapura és 1 db 4 bemenetű ÉS kapura van szükség.
- Azt is olvashatja: Negatív visszacsatolású és negatív visszacsatolású erősítőrendszerek
Az összeg szorzatának (POS)
Az összeg szorzata kifejezés sajátos sematikus felépítése OR-AND. Az OR-AND-ben a bemenetek egy OR kapukból álló tömbön mennek keresztül, amely a kapuk első szintje, az első szintű OR kapuk kimenete a kapu második szintjén megy keresztül,amely egy AND kapu.
Az ebben a konstrukcióban használt bemenetek és kapuk száma a megvalósítandó kifejezéstől függ.
A kanonikus forma a lehetséges bemenetek és kapuk maximális számából áll,a minimális forma azonban a lehető legkisebb számú bemenetből és kapuból áll. A kanonikus és a minimális POS-forma sematikus felépítése az alábbiakban látható.
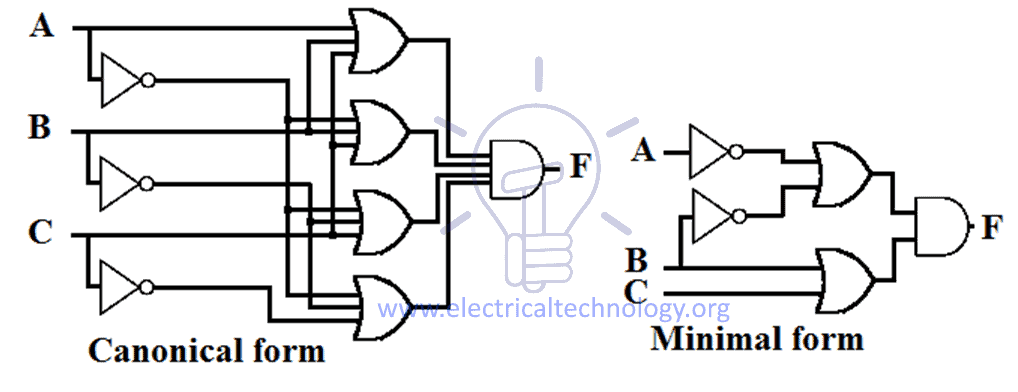
Konvertálás a minimális POS-ból a kanonikus POS-formába
Amint tudjuk, a POS kanonikus formája maximális kifejezésekkel rendelkezik, és a maximális kifejezések minden bemenetet tartalmaznak akár kiegészítve, akár nem kiegészítve. Tehát minden összegtermet a kiegészített és a nem kiegészített hiányzó bemenet szorzatával adunk össze. Az átalakításra az alábbi példa látható.
Minimális POS forma
F = (A̅+B̅) (B+C)
(A̅+B̅) terminus hiányzik a C bemenetből, ezért hozzáadjuk a (CC̅) terminust. A (B+C) kifejezésből hiányzik az A bemenet, ezért hozzáadjuk az (AA̅) kifejezést.
F = (A̅+B̅+CC̅) (B+C+AA̅)
F = (A̅+B̅+C)(A̅+B̅+C̅)(A+B+C)(A̅+B+B+C)
Ez a kifejezés most már kanonikus formában van.
- Az is olvasható: Számláló és az elektronikus számlálók típusai
Konvertálás kanonikus POS-ból SOP-ba
Az összeg szorzata kifejezés csak akkor konvertálható összeg szorzata formába, ha a kifejezés kanonikus formában van. A kanonikus POS és a kanonikus SOP egymásba konvertálható, azaz egymásba konvertálhatók. Az alábbiakban példát adunk a POS-ból SOP-ba való átalakításra.
POS kanonikus forma
F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+B̅+C̅)
A kanonikus formában minden egyes összegtag egy max tag, tehát így is írható:
F = ∏(M0,M4,M6,M7)
A bemenetek fennmaradó kombinációi a függvény olyan mintermei, amelyeknek a kimenete igaz. Ahhoz, hogy SOP-kifejezéssé alakítsuk át, először a jelet összegzésre (∑) változtatjuk, és a maradék mintermeket használjuk.
F = ∑ (m1,m2,m3,m5)
Most az összegző jelet kibővítjük, hogy kanonikus SOP-kifejezést alkossunk.
F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C
Min kifejezések a Max kifejezések komplementerei azonos bemeneti kombináció esetén.
Kanonikusból Minimális POS
A kanonikus összegtermék kifejezés Karnaugh térkép (K-térkép) segítségével átalakítható Minimális összegtermék formára. Egy másik módszer a kanonikus alakzat minimálissá alakítására a Boole algebrai tételek segítségével.
A K-térkép használata nagyon egyszerű, ezért a K-térképet részesítik előnyben. A minimális POS-kifejezéshez a K-térképben a 0-kat csoportokká kombináljuk, és a kapott kifejezés komplementer, mivel a csoportokat ‘0-kból állították össze. A példája fentebb megtörtént.
Az alábbiakat is olvashatja:
- Digitális logikai NOT kapu – Digitális inverter logikai kapu
- Exkluzív-NOR (XNOR) digitális logikai kapu
- Digitális logikai NOR kapu
- Digitális logikai NAND kapu
Vélemény, hozzászólás?